mathematicsSimilar presentations:
Лекция №11 по курсу «Машинная арифметика в рациональных числах»
1.
Лекция №11по курсу
«Машинная арифметика в рациональных
числах»
Лектор: д.т.н., Оцоков Шамиль Алиевич,
email: [email protected]
Москва, 2021
2.
Правила интервальные вычисления(Достоверные вычисления)
Арифметические операции над интервалами выражаются через операции
над парами чисел, задающими их границы. Округление при вычислении
нижней границы осуществляется с недостатком, а верхней с избытком.
Интервал гарантированно содержит истинный результат
Вычисления с интервалами:
3.
Интервальные вычисления(Достоверные вычисления)
Автоматическая верификация результатов
Доказательство корректности вычислительных задач.
(гипотезы теории хауса, Кеплера и др.)
(Не влияют на корректность алгоритма)
Направленные округления:
1. Нижняя граница – результат округления до ближайшего машинного
числа с плавающей точкой с недостатком
2. Верхняя граница – результат округления до ближайшего машинного
числа с плавающей точкой с избытком
4.
Интервальные вычисления(Достоверные вычисления)
Проблема расширения интервалов в процессе вычислений.
Примеры задач где они применяются
- Гарантированное нахождение всех нулей нелин. функции
- Глобальная оптимизация с подтверждением правильности нахождения
минимума
5.
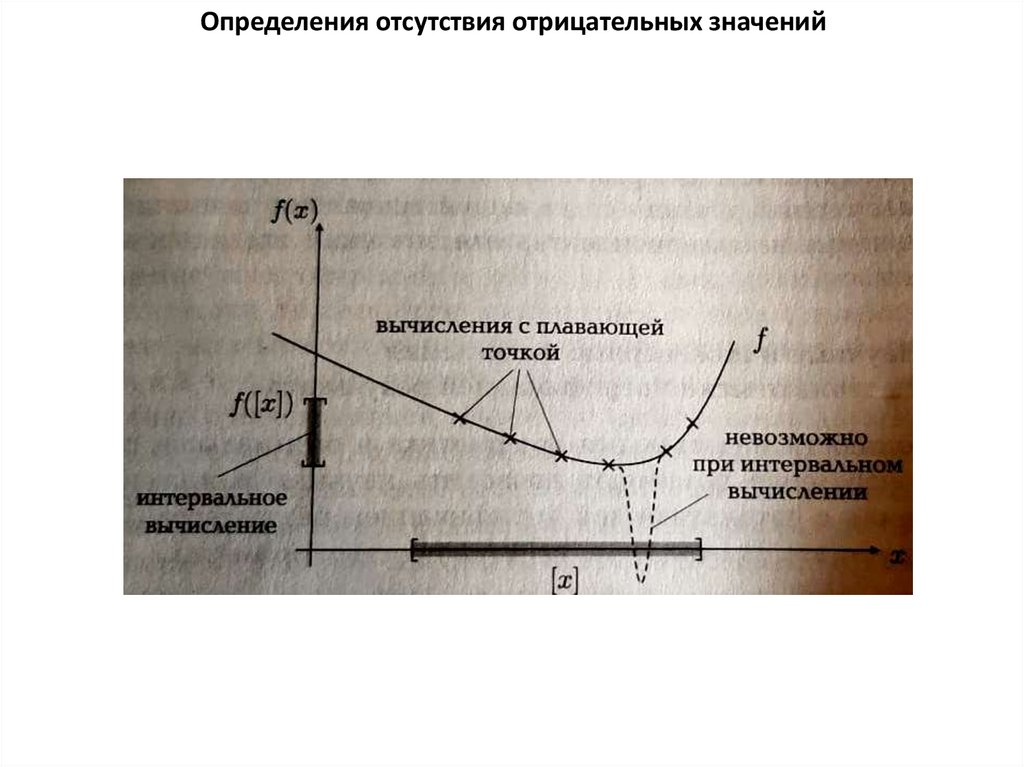
Определения отсутствия отрицательных значений6.
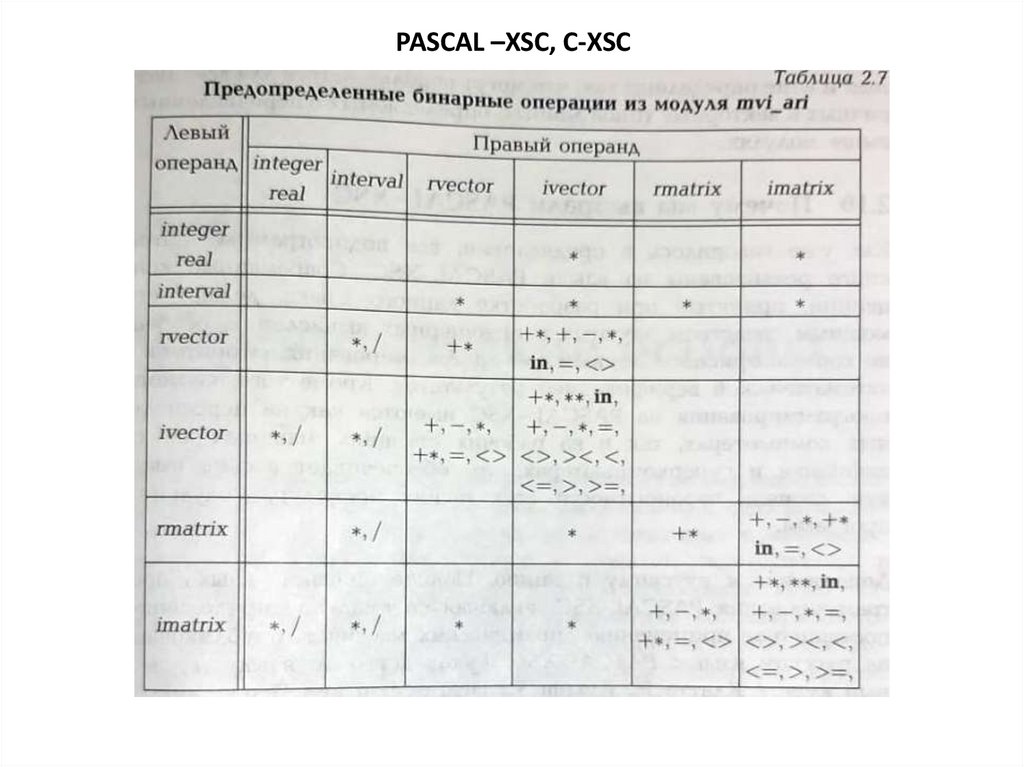
PASCAL –XSC, C-XSCPASCAL Extension for Scientific Computation
Некоторые типы данных:
complex, interval, cinterval, rvector, cvector, ivector, rmatrix, imatric
dotprecision – числа с фиксированной точкой, покрывающие весь
возможный диапазон представления чисел c плавающей точкой.
(< +- Мантисса E показатель) – округление с недостатком
(> +- Мантисса E показатель) – округление с избытком
yyy…yyy, xxxxx..x (38 – кол десят разрядов целой части, 38 – кол дес
дробной части)
0,123
123,456
(X,Y) = x1*y1+x2*y2+…+xn*yn
X = (x1,x2,…,xn)
Y = (y1,y2,…,yn)
7.
PASCAL –XSC, C-XSCИнтервальная арифметика – модуль i_ari
Арифметика матриц и векоторов mv_ari
(< +- Мантисса E показатель) – округление с недостатком
(> +- Мантисса E показатель) – округление с избытком
8.
PASCAL –XSC, C-XSC9.
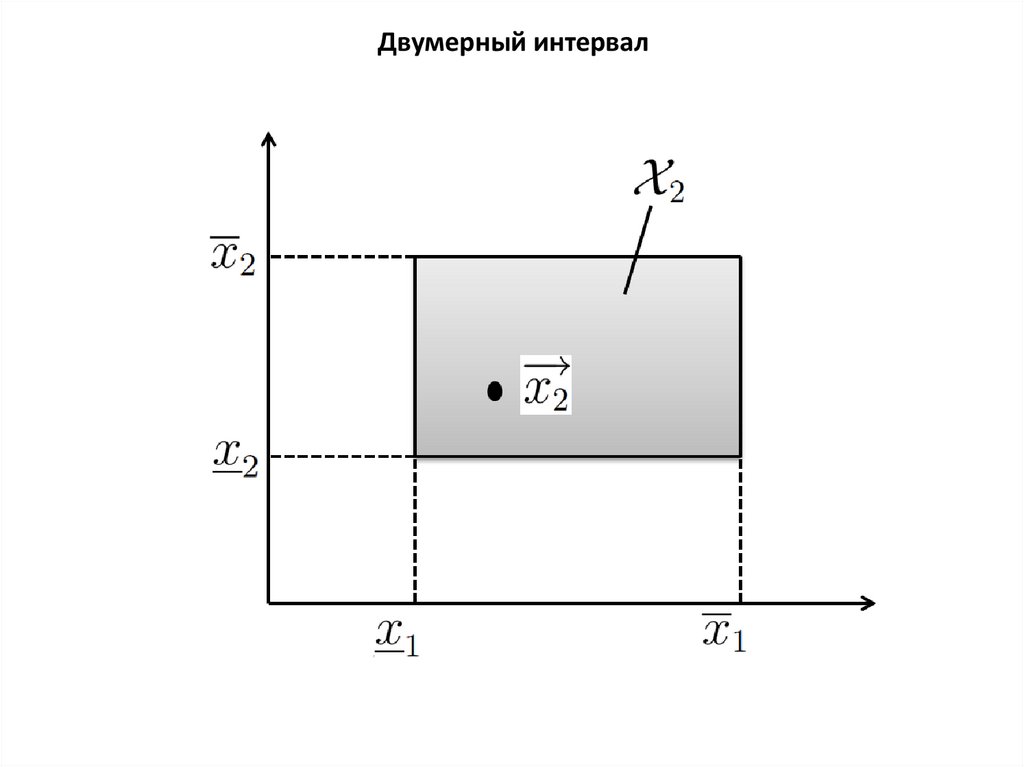
Двумерный интервал10.
Теоретические основы интервальных вычисленийМножество чисел внутри интервала бесконечное