Разработка модели развития дефекта на границе раздела фаз в стеклопластике на основе термопластичной матрицы

1. Разработка Модели развития дефекта на границе раздела фаз в стеклопластике на основе термопластичной матрицы, модифицированной наночаст

Министерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального
образования
МАИ (национальный исследовательский институт)
Кафедра ТКМ,К и М
РАЗРАБОТКА МОДЕЛИ РАЗВИТИЯ ДЕФЕКТА НА ГРАНИЦЕ РАЗДЕЛА
ФАЗ В СТЕКЛОПЛАСТИКЕ НА ОСНОВЕ ТЕРМОПЛАСТИЧНОЙ
МАТРИЦЫ, МОДИФИЦИРОВАННОЙ НАНОЧАСТИЦАМИ
Козлова С.О.,
гр.1МТМ-2ДМ-015
Научный Руководитель:
к.н.т., доц. Салиенко Н.В.
Москва, 2016

2. Цель дипломного проекта

ЦЕЛЬ ДИПЛОМНОГО ПРОЕКТА
2
Разработка модели развития дефекта на границе раздела фаз в
стеклопластике на основе термопластичной матрицы, модифицированной
наночастицами слоистого алюмосиликата монтмориллонита (ММT)

3. Задачи:

ЗАДАЧИ:
- Провести анализ литературных данных типов наноматериалов, наноглин и ПКМ на их
основе, особенностей свойств наноструктур, особенностей получения нанокомпозитов,
наномодификации ПА-6. Проанализировать стеклянные волокна с точки зрения
использования в качестве армирующих в ПКМ.
- Рассмотреть основы прочности композитов, армированных непрерывными волокнами и
определить теоретическую базовую модель для прогнозирования деформационнопрочностных свойств ПКМ. Определить метод расчёта модуля упругости полимерной
матрицы модифицированной наночастицами.
- Разработать физическую модель структуры ПКМ с модифицированной минеральными
наночастицами термопластичной матрицей и непрерывными стеклянными волокнами.
- Исследовать с помощью разработанной модели влияние наномодификации в матрице и
наличия дефекта на границе раздела фаз на деформационно-прочностные свойств
стеклопластика.
3
- Провести анализ и верификацию полученных данных.

4. Задачи литературного обзора

ЗАДАЧИ ЛИТЕРАТУРНОГО ОБЗОРА
Провести анализ литературных данных о:
- дефектах в монолитных и слоистых конструкциях из ПКМ;
- типах наноматериалов, наноглин и ПКМ на их основе;
- особенностях
свойств
наноструктур,
особенностей
получения
нанокомпозитов,
наномодификации ПА-6;
- проанализировать стеклянные волокна с точки зрения использования в качестве армирующих в
ПКМ;
Определить теоретическую базовую модель для прогнозирования деформационно-прочностных
свойств ПКМ и метод расчёта модуля упругости полимерной матрицы модифицированной
наночастицами.
4
Рассмотреть:
- метод конечных элементов при моделировании ПКМ;
- принципы разбиения моделей на КЭ;
- подходы в моделировании ПКМ;
- модели ПКП для блочного метода;
- подходы моделирования для прогнозирования роста трещин.

5. 1. Дефекты в монолитных и многослойных конструкциях из ПКМ

1. ДЕФЕКТЫ В МОНОЛИТНЫХ И МНОГОСЛОЙНЫХ
КОНСТРУКЦИЯХ ИЗ ПКМ
Кроме макродефектов, в ПКМ присутствуют дефекты на
уровне микроструктуры: поры (зоны повышенной
пористости), в зоне которых отмечается пониженная
прочность материала.
Степень опасности этих дефектов зависит в конечном
счете от размера, формы и расположения дефекта.
5
Прерывистость расслоения углепластика

6. Стекловолокна с точки зрения их использования в ПКМ

СТЕКЛОВОЛОКНА С ТОЧКИ ЗРЕНИЯ ИХ ИСПОЛЬЗОВАНИЯ В ПКМ
Плотность
Предел прочности при
Модуль
Удельная
г/см 3
растяжении
упругости
Прочность
МПа
ГПа
м
2,48
125—25
200—700
5 000—10 000
Крафтцеллюлозное
-
91
785
-
Вискозное вытянутое
-
7 5,6
86,9
-
Найлоновое
1,14
5 0,4
46
4 400
Хлопчатобумажное
1,54
4 7,6
77
3 080
Волокно
Стеклянное
6
Некоторые физико-механические свойства различных волокон

7. Стекловолокна с точки зрения их использования в ПКМ

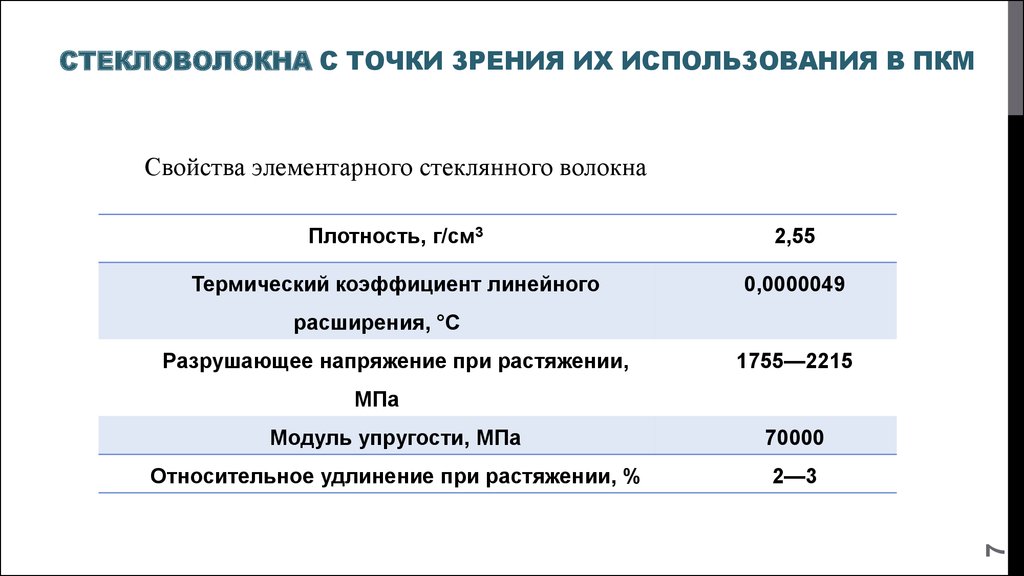
СТЕКЛОВОЛОКНА С ТОЧКИ ЗРЕНИЯ ИХ ИСПОЛЬЗОВАНИЯ В ПКМ
Свойства элементарного стеклянного волокна
Плотность, г/см3
2,55
Термический коэффициент линейного
0,0000049
расширения, °С
Разрушающее напряжение при растяжении,
1755—2215
Модуль упругости, МПа
70000
Относительное удлинение при растяжении, %
2—3
7
МПа

8. Термопластичные матрицы

ТЕРМОПЛАСТИЧНЫЕ
МАТРИЦЫ
Термопластичная матрица в ТПКМ:
- обеспечивает монолитность материала, прочную связь между
армирующими элементами и их совместную работу при нагружении;
- лимитирует деформационную теплостойкость и термостойкость
материала;
- вносит аддитивный вклад в эксплуатационные свойства материала;
8
- играет определяющую роль в выборе и реализации метода и условий
формования элементов конструкций.

9. Типы наноматериалов и их общая характеристика

9
ТИПЫ НАНОМАТЕРИАЛОВ И ИХ ОБЩАЯ
ХАРАКТЕРИСТИКА

10. Особенности получения полимерных наноматериалов

ОСОБЕННОСТИ ПОЛУЧЕНИЯ ПОЛИМЕРНЫХ НАНОМАТЕРИАЛОВ
Получение полимерных нанокомпозитов с минеральными наноразмерными наполнителями
1. Местная полимеризация.
2. Перемешивание расплава.
10
3. Перемешивание раствора.

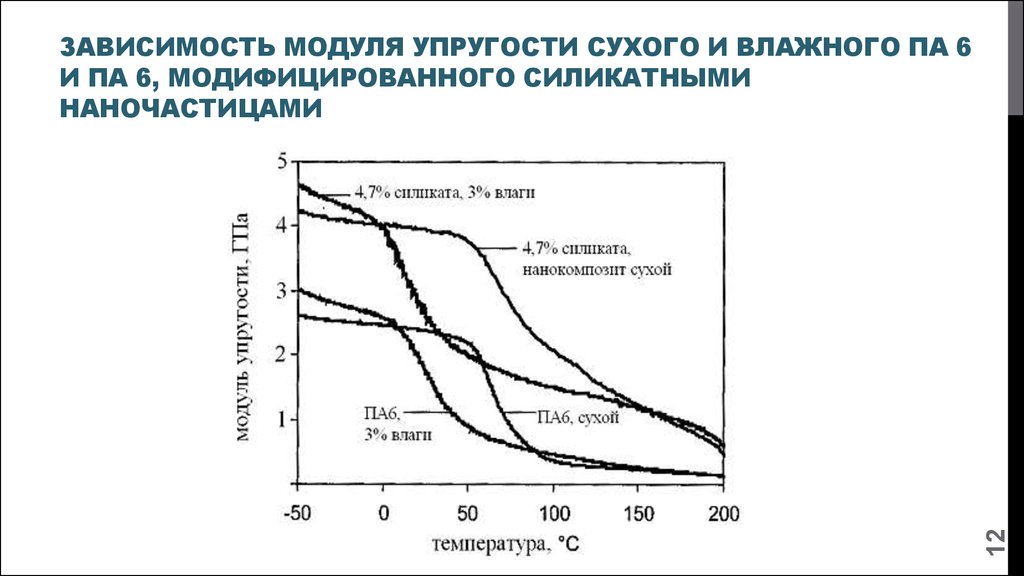
11. Свойсва модифицированного наночастицами ПА 6 Влияние концентрации силиката и влаги на модуль упругости нанокомпозита

11
СВОЙСВА МОДИФИЦИРОВАННОГО НАНОЧАСТИЦАМИ ПА 6
ВЛИЯНИЕ КОНЦЕНТРАЦИИ СИЛИКАТА И ВЛАГИ НА МОДУЛЬ
УПРУГОСТИ НАНОКОМПОЗИТА

12. Зависимость модуля упругости сухого и влажного ПА 6 и ПА 6, модифицированного силикатными наночастицами

12
ЗАВИСИМОСТЬ МОДУЛЯ УПРУГОСТИ СУХОГО И ВЛАЖНОГО ПА 6
И ПА 6, МОДИФИЦИРОВАННОГО СИЛИКАТНЫМИ
НАНОЧАСТИЦАМИ

13. Метод конечных элементов в моделировании ПКМ

МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ В
МОДЕЛИРОВАНИИ ПКМ
1. Область определения непрерывной функции разбивается на конечное число подобластей (элементов). Эти
элементы составляют область и имеют общие точки (узлы).
2. В рассматриваемой области фиксируется конечное число точек (узлов). В этих точках вводятся фиктивные
силы, эквивалентные поверхностным напряжениям, распределенным по границам элементов. Элементы
взаимодействуют между собой только в узловых точках.
3. Первоначальное значение непрерывной функции в узловых точках предполагается известным.
4. Для каждого из элементов области определяется аппроксимирующая функция (функция элемента). Чаще
всего она выбирается в виде линейных, квадратичных или кубических полиномов. Для каждого элемента
можно подбирать свой полином, однако должно выполняться условие непрерывности функции вдоль границ
элемента.
5. На множестве узлов опять задаются значения функции, на этот раз являющиеся переменными. Узловые
значения функции выбираются из условия минимизации функции, связанной с физической природой задачи.
Например, в прочностных задачах, где определяются поля перемещений, деформаций и напряжений,
минимизируется потенциальная энергия деформируемого тела. Процесс минимизации сводится к решению
систем линейных алгебраических уравнений относительно значений функции в выбранных узлах.
13
Порядок построения дискретной модели состоит из следующих этапов:

14. Решение задачи по МКЭ состоит из следующих этапов:

РЕШЕНИЕ ЗАДАЧИ ПО МКЭ СОСТОИТ ИЗ
СЛЕДУЮЩИХ ЭТАПОВ:
Постановка задачи.
Создание геометрии.
Разбиение модели на сетку конечных элементов.
Приложение к модели условий закрепления и нагружения. Задание начальных
условий в случае динамического анализа.
5. Численное решение системы уравнений.
6. Анализ полученных результатов.
1.
2.
3.
4.
14
Этапы 1-4 относятся к препроцессорной стадии, этап 5 – к процессорной стадии,
этап 6 – к постпроцессорной стадии.

15. Микроподход в моделировании ПКМ. Блочный метод

При применении метода конечных элементов для
композитов
с
учетом
указанного
выше
обстоятельства
эффективным
оказывается
блочный метод.
Модель ПКМ, армированного волокном.
15
В блочном методе при разбиении выделяются
1 — матрица (смола)
целые области, которые затем разбиваются на
2 — армирующий элемент (волокно)
элементы. Для каждой такой области полагают,
что
постоянные
материала
являются
Распределение эквивалентных напряжений на конце
неизменными. Следовательно, если имеются
волокна
разнородные материалы, то в таком случае
разбиение на области желательно проводить по
материалам.
Одним из блоков является армирующее волокно.

16. Аналитическое моделирование деформационно-прочностных свойств полимерной композиционной матрицы

Аналитическое моделирование деформационнопрочностных свойств полимерной композиционной матрицы
Модель Ирвина-Орована
KI
2
2 y
2
) cos 2
(4(1 )) 3 cos 2 )
2
2
Схема распределения напряжений вблизи кончика
трещины при развитии локальной пластической
зоны
Модель неупругого (упруго-пластического)
поведения трещины
16
rу (
Модель Дагдейла

17. Аналитическое моделирование деформационно-прочностных свойств полимерной композиционной матрицы

Аналитическое моделирование деформационнопрочностных свойств полимерной композиционной матрицы
Модель Баренблатта
(б)
(а)
Схемы общего вида трещины в хрупком теле с когезионной зоной в модели Баренблатта (а) и плавного
Максимальное значение сил когезионного сцепления
соответствует прочности атомно-молекулярных связей
(идеальной локальной прочности тела) и примерно равно
с
Е
Е s
b
17
смыкания берегов трещины у ее края (б) .

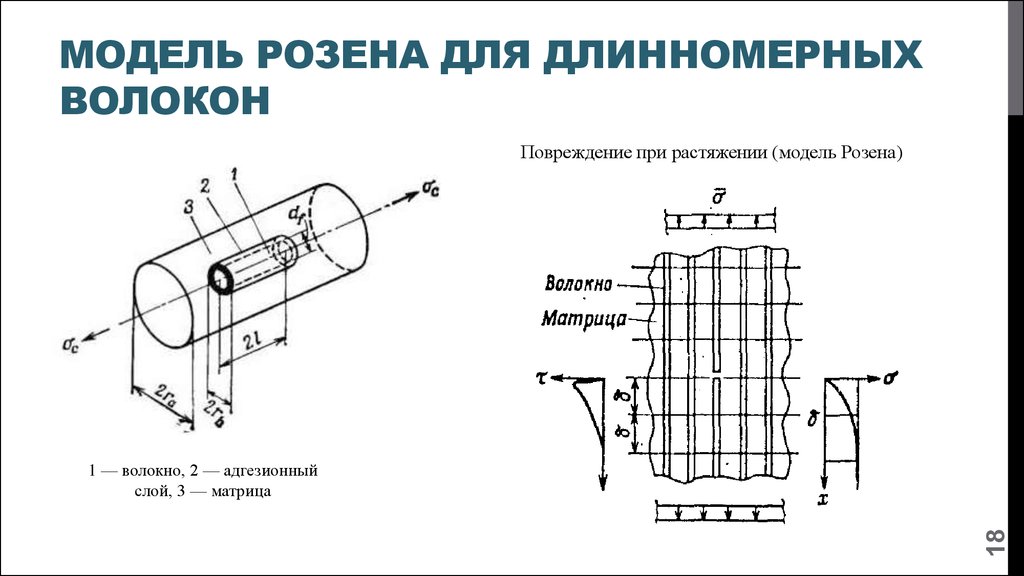
18. Модель Розена для длинномерных волокон

МОДЕЛЬ РОЗЕНА ДЛЯ ДЛИННОМЕРНЫХ
ВОЛОКОН
Повреждение при растяжении (модель Розена)
18
1 — волокно, 2 — адгезионный
слой, 3 — матрица

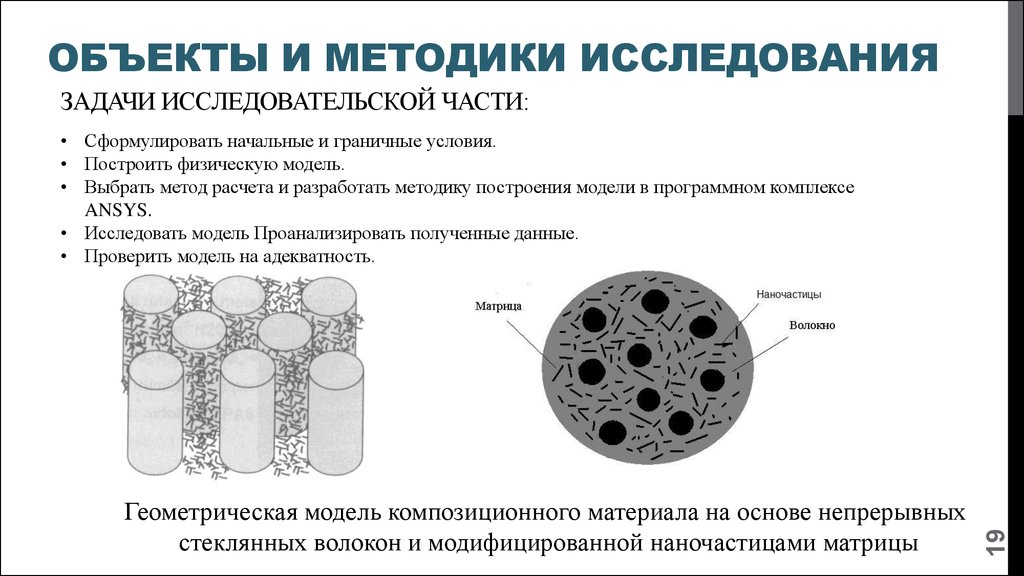
19. Объекты и методики исследования

ОБЪЕКТЫ И МЕТОДИКИ ИССЛЕДОВАНИЯ
ЗАДАЧИ ИССЛЕДОВАТЕЛЬСКОЙ ЧАСТИ:
Геометрическая модель композиционного материала на основе непрерывных
стеклянных волокон и модифицированной наночастицами матрицы
19
• Сформулировать начальные и граничные условия.
• Построить физическую модель.
• Выбрать метод расчета и разработать методику построения модели в программном комплексе
ANSYS.
• Исследовать модель Проанализировать полученные данные.
• Проверить модель на адекватность.

20. Объекты и методики исследования

ОБЪЕКТЫ И МЕТОДИКИ ИССЛЕДОВАНИЯ
ЗАДАЧИ ИССЛЕДОВАТЕЛЬСКОЙ ЧАСТИ:
20
• Сформулировать начальные и граничные условия.
• Построить физическую модель.
• Выбрать метод расчета и разработать методику построения
модели в программном комплексе ANSYS.
• Исследовать модель
• Проанализировать полученные данные.
• Проверить модель на адекватность.

21. Допущения принятые в модели:

ДОПУЩЕНИЯ ПРИНЯТЫЕ В МОДЕЛИ:
все непрерывные волокна ориентированы в одном направлении;
волокна расположены таким образом, что перераспределение
напряжений осуществляется и с помощью поперечных деформаций;
модель содержит наночастицы размеры которых не учитываются;
расчёт модуля упругости Em полимерной матрицы модифицированной
наночастицами осуществляется методом Халпина – Цая (так же для
сравнения был использован метода Льюиса и Нильсона);
модель осесимметрична
Следующие параметры могут свободно варьироваться:
диаметр волокна df
объемное содержание волокна Vf
модуль упругости (Ef, Em,) и коэффициент Пуасона ( f, m)
пластичность матрицы задана графически (зависимость «напряжениедеформация»).
21

22. Физическая модель ПКМ на основе непрерывных волокон и поликапроамидной матрицы при одноосном растяжении вдоль волокна

ФИЗИЧЕСКАЯ МОДЕЛЬ ПКМ НА ОСНОВЕ НЕПРЕРЫВНЫХ ВОЛОКОН И
ПОЛИКАПРОАМИДНОЙ МАТРИЦЫ ПРИ ОДНООСНОМ РАСТЯЖЕНИИ ВДОЛЬ
ВОЛОКНА
22
Объекты исследования

23. Расчёт модуля упругости полимерной матрицы модифицированной наночастицами методом Халпина–Цая

РАСЧЁТ МОДУЛЯ УПРУГОСТИ ПОЛИМЕРНОЙ МАТРИЦЫ
МОДИФИЦИРОВАННОЙ НАНОЧАСТИЦАМИ МЕТОДОМ ХАЛПИНА–ЦАЯ
Ec 1 f
Em 1 f
( E f / Em ) 1
( E f / Em )
23
где Ес – модуль упругости комозита, Еf - модуль упругости частиц, Em- модуль упругости матрицы,
- коэффициент формы, зависящий от геометрии, ориентации и коэффициента, Пуассона частиц,
- объемная доля наполнителя, f - коэффициент Пуассона композиционного материала

24. Методика построения модели в программном пакете ANSYS:

Подготовка модели (Preprocessing)
1.Запуск Ansys.
2.Установка фильтров меню.
3.Назначение типов конечных элементов (КЭ) и их особенности.
4.Определение свойств материала модели
5.Создание геометрической модели
6.Присвоение блокам свойств волокна и матрицы
7.Разбиение модели на КЭ.
8.Задание граничных условий.
8.1 Перемещения (Displacement) на верхней и нижней границах
модели
8.2 Соединение узлов между собой с ограничением степеней
свободы (Coupling DOF) на левой, правой границах модели и
границе раздела
Решение (Solving)
9. Расчёт
Анализ результатов (Postprocessing)
10. Отображение деформированного и недеформированного
состояния модели.
11. Отображение полей напряжений и деформаций. Отображение
полей напряжений по Von Mises
12. Одновременное отображение графической и численной
информации о напряжениях и деформации
13. Выход из Ansys
24
МЕТОДИКА ПОСТРОЕНИЯ МОДЕЛИ В ПРОГРАММНОМ ПАКЕТЕ ANSYS:

25. Методика построения модели в программном пакете ANSYS:

МЕТОДИКА ПОСТРОЕНИЯ МОДЕЛИ В
ПРОГРАММНОМ ПАКЕТЕ ANSYS:
Ввод данных для ортотропного материла
25
Выбор нового материала

26. Конечно-элементная модель

26
КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ

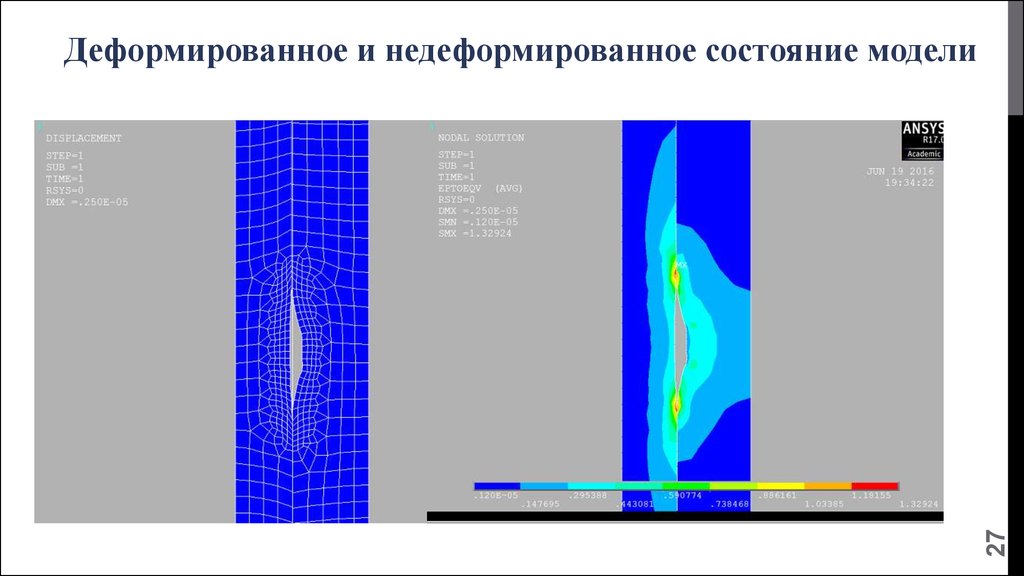
27.

27
Деформированное и недеформированное состояние модели

28.

28
Деформированние модели. Анимация.

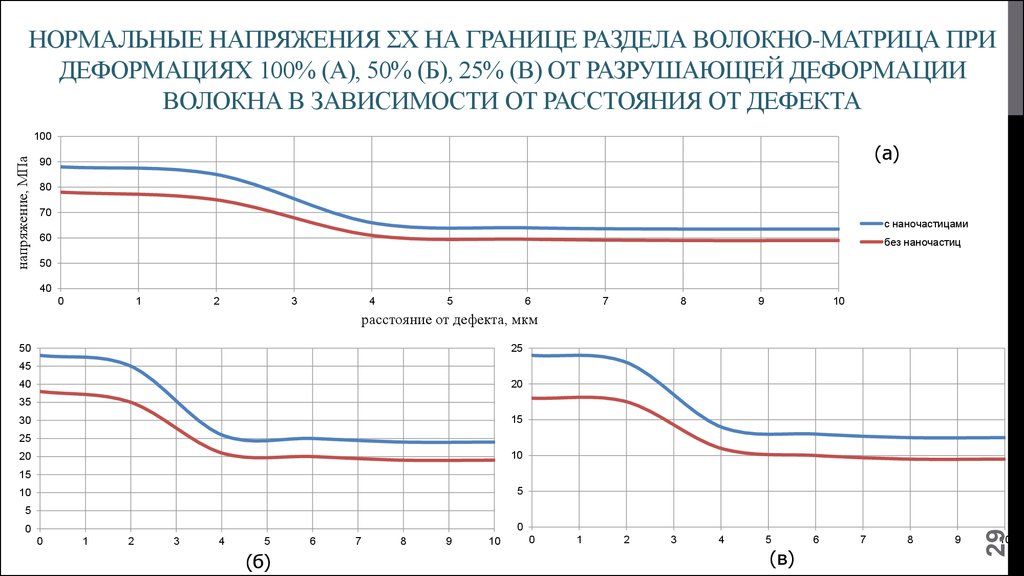
29. Нормальные напряжения ςх на границе раздела волокно-матрица при деформациях 100% (а), 50% (б), 25% (в) от разрушающей деформации волокна в зависимо

НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ ΣХ НА ГРАНИЦЕ РАЗДЕЛА ВОЛОКНО-МАТРИЦА ПРИ
ДЕФОРМАЦИЯХ 100% (А), 50% (Б), 25% (В) ОТ РАЗРУШАЮЩЕЙ ДЕФОРМАЦИИ
ВОЛОКНА В ЗАВИСИМОСТИ ОТ РАССТОЯНИЯ ОТ ДЕФЕКТА
напряжение, МПа
100
(а)
90
80
70
с наночастицами
60
без наночастиц
50
40
0
1
2
3
4
5
6
7
8
9
10
расстояние от дефекта, мкм
50
25
45
20
40
35
15
30
25
10
20
15
5
10
0
0
0
1
2
3
4
5
(б)
6
7
8
9
10
0
1
2
3
4
5
(в)
6
7
8
9
29
5
10

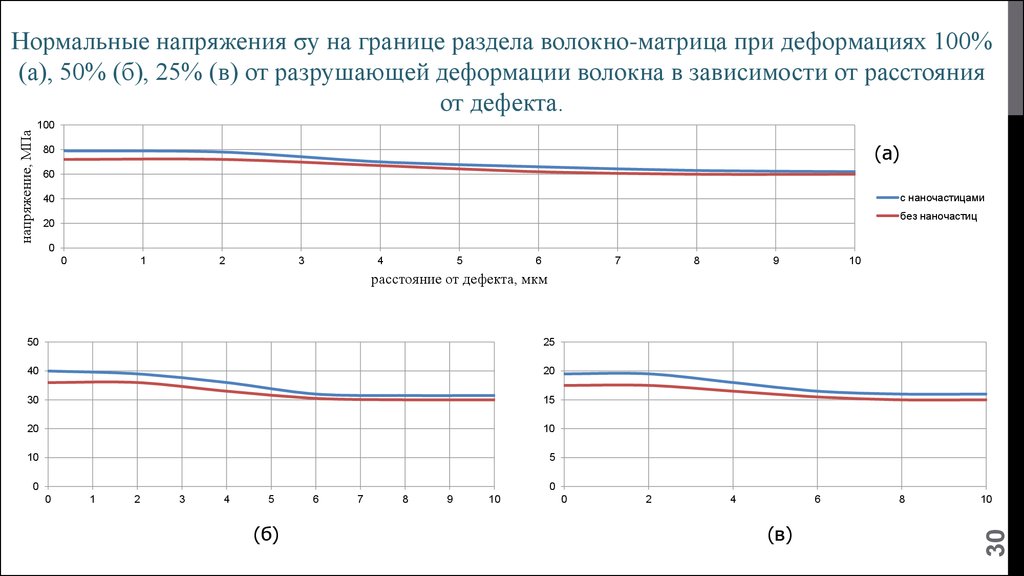
30.

напряжение, МПа
Нормальные напряжения σу на границе раздела волокно-матрица при деформациях 100%
(а), 50% (б), 25% (в) от разрушающей деформации волокна в зависимости от расстояния
от дефекта.
100
(а)
80
60
с наночастицами
40
без наночастиц
20
0
0
1
2
3
4
5
6
7
8
9
10
расстояние от дефекта, мкм
50
25
40
20
30
15
20
10
10
5
0
0
1
2
3
4
5
(б)
6
7
8
9
10
0
2
4
6
(в)
8
10
30
0

31.

Сдвиговые напряжения τху на границе волокно – матрица при деформации 100% (а), 50%
(б), 25% (в) от разрушающей деформации волокна в зависимости от расстояния от дефекта.
15
10
5
0
0
1
-5
2
3
4
5
6
7
8
9
расстояние от дефекта, мкм
6
5
4
3
2
1
0
-1 0
-2
1
2
3
4
5
6
7
8
расстояние от дефекта, мкм
а
б
5
4
3
2
с наночастицами
1
без наночастиц
0
-1
-2
0
1
2
3
4
5
6
7
8
расстояние от дефекта, мкм
в
31
напряжение, МПа
6

32.

В результате проведенных исследований:
Разработана модель развития дефекта на границе раздела фаз в стеклопластике на основе
термопластичной поликапроамидной матрицы, модифицированной наночастицами слоистого алюмосиликата
монтмориллонита.
Установлено, что модификация наночастицами, позволяет повысить значение модуля упругости, достичь
равномерного перераспределения напряжений с матрицы на волокна, достичь снижения уровня остаточных
напряжений в зоне контакта порожденных усадкой матрицы в процессе охлаждения и различием в модулях
упругости; улучшить совместимость компонентов ПКМ.
С помощью пакета прикладных программ ANSYS получены поля напряжений в материале при сложном
одноосном растяжении. Получены графические зависимости изменения напряжений в зависимости от
расстояния до дефекта. Анализ показал, что модификация матрицы наночастицами позволяет достичь
равномерного перераспределения напряжений. Апробация модели показала, что полученные данные хорошо
коррелируют со значениями из литературных источников.
начальных условий и исключения допущений, а также оптимизации путем варьирования параметров.
32
Полученная модель может быть использована для дальнейшего усовершенствования путем уточнения

33. Сравнение экспериментальных данных

СРАВНЕНИЕ ЭКСПЕРИМЕНТАЛЬНЫХ
ДАННЫХ
Напряжения σ+
МПа
Моделирование
Справочные данные
Не
модифицированная
матрица
Модифицированная
Не
модифицированная
матрица
Модифицир
ованная
75
88
78
82
33
Параметр

34.

34
Спасибо за внимание!