Лабораторная работа «Простые методы статистической оптимизации»

1.

Самарский государственный технический университет
Инженерно-технологический факультет
Кафедра «Химия и технология органических соединений азота»
Лабораторная работа
«Простые методы статистической оптимизации»
Copyright © доцент А.К.Тарасов
Редакция 23.07.13

2. Методические указания к лабораторным практикумам по курсам «Информационные технологии в химии и производстве ЭНМ» и

2
Методические указания к лабораторным практикумам по курсам «Информационные технологии
в химии и производстве ЭНМ» и «Хемометрика».
Сост. А.К.Тарасов – Самара; Самар. гос. техн. ун-т; 2013. -80 кадров.
Содержат рекомендации о порядке выполнения лабораторной работы
«Простые методы статистической оптимизации» по курсам «Информационные технологии в
химии и производстве ЭНМ» (240301) и «Хемометрика» (280700).
Методические указания предназначены для студентов специальностей 240301 и 280700
инженерно-технологического факультета.

3. Цель работы Целью данной работы является освоение статистических методов оптимизации технологических процессов по

3
Цель работы
Целью данной работы является освоение статистических методов
оптимизации технологических процессов по Гауссу-Зайделю и симплекс-методом
с применением имитационного эксперимента.
Для выполнения данной работы используются файлы таблицы Excel.
Данные методические указания представляют из себя комплекс, в котором интегрированы
обучающие модули типа презентаций Power Point и файлы-шаблоны Excel, в которых и
выполняются упражнения.
Запуск обучающих модулей и открытие файлов-шаблонов выполняется с помощью
гиперссылок из обучающих модулей.
Отчетом по выполненной работе является файл Excel с выполненным упражнением,
сохраненный студентом в папке соответствующей группы (D:\Лабораторные
занятия\Курс\Группа\...)

4. Порядок выполнения работы

Работа состоит из четырех разделов (обучающих модулей).
Изучите содержание каждого раздела и выполните указанные в них упражнения.
При выполнении работы переключайтесь между окном программы Excel и окном
обучающего модуля с помощью команды Alt –Tab.
Упражнение 1. Сущность методов шаговой оптимизации
Упражнение 2. Оптимизация по методу Гаусса-Зайделя»
Упражнение 3. Оптимизация симплекс-методом
4

5.

5
Упражнение 1.
Сущность методов шаговой оптимизации

6. Сущность методов шаговой оптимизации

6
Оптимизация технологического процесса - процесс поиска условий его проведения с
наибольшей эффективностью при минимальных затратах
при соблюдении заданных
ограничений.
Различают эмпирический и детерминированный подходы к оптимизации.
Детерминированный подход применяется при наличии хорошей достаточно полной
математической модели оптимизируемого процесса.
Сущность такого подхода - теоретический расчет оптимальных условий на основании
системы уравнений математической модели процесса.
Эмпирический (опытный) подход эффективен при отсутствии хорошей модели процесса (а в
некоторых случаях и при ее наличии).
Одна из основных идей оптимизации при эмпирическом (опытном) подходе заключается в
следующем. Факторы, влияющие на процесс изменяют по определенному алгоритму, причем не
непрерывно, а шагами.
Каждый шаг - опыт. Сравнивая результаты данного опыта с результатами предыдущих,
принимаем решение о дальнейших действиях по поиску оптимума
Процесс оптимизации напоминает “движение” в n-мерном пространстве независимых
переменных (факторов, влияющих на оптимизируемый процесс).
Это сущность алгоритмов шаговой оптимизации.
Такие методы оптимизации называют «статистическими».

7. Сущность методов шаговой оптимизации

Данное упражнение выполняется в среде Excel.
Откройте файл-шаблон упражнения с помощью приведенной ниже гиперссылки.
Ссылка для файла-шаблона данного упражнения
7

8.

8
Упражнение 2.
Оптимизация по методу Гаусса-Зайделя

9. Оптимизация по методу Гаусса-Зайделя

Изучите методику работу с имитатором реального эксперимента.
В конце этого раздела будет ссылка на запуск программы-имитатора,
Сначала просмотрите, как с ней работать.
9

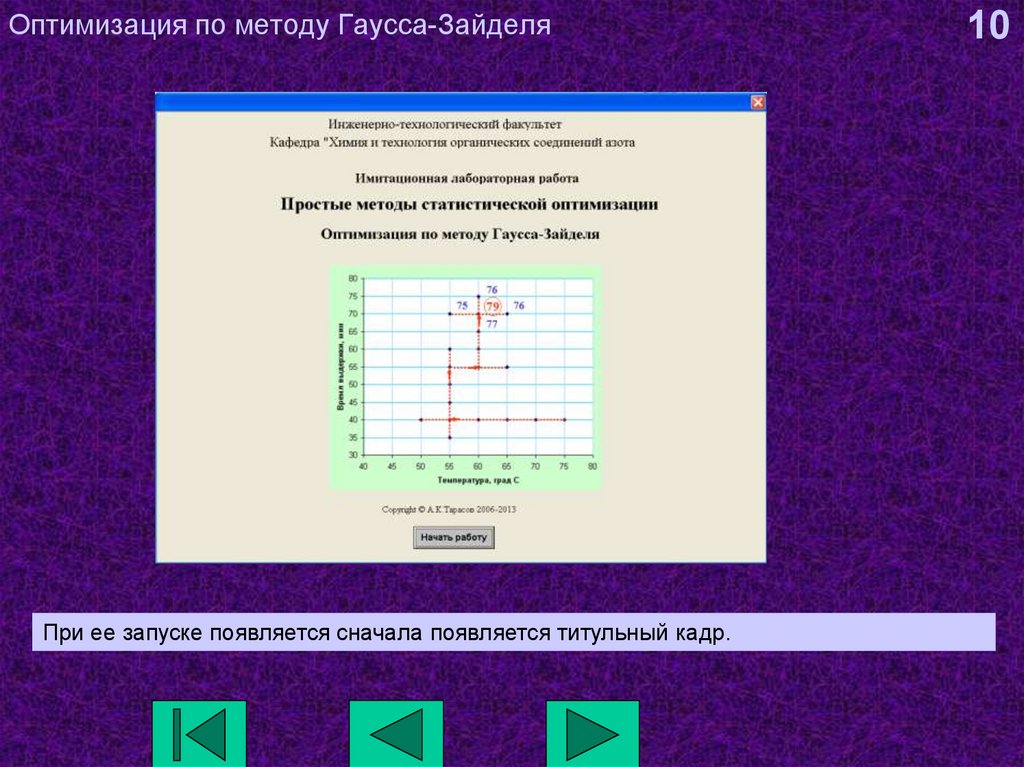
10. Оптимизация по методу Гаусса-Зайделя

При ее запуске появляется сначала появляется титульный кадр.
10

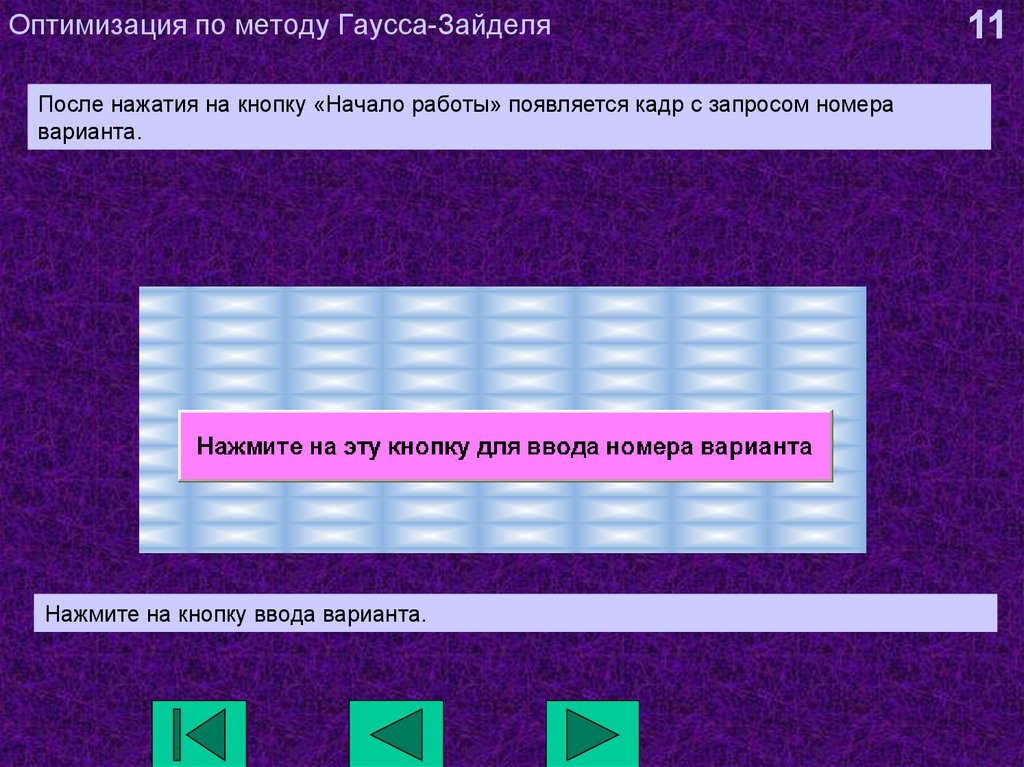
11. Оптимизация по методу Гаусса-Зайделя

После нажатия на кнопку «Начало работы» появляется кадр с запросом номера
варианта.
Нажмите на кнопку ввода варианта.
11

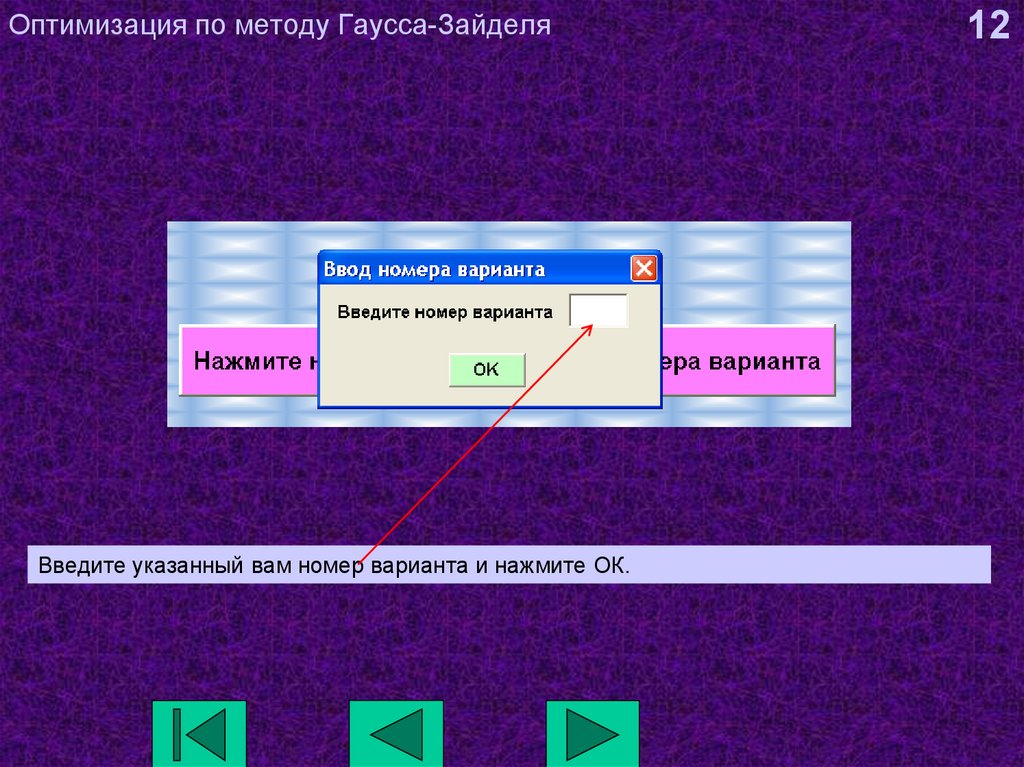
12. Оптимизация по методу Гаусса-Зайделя

Введите указанный вам номер варианта и нажмите ОК.
12

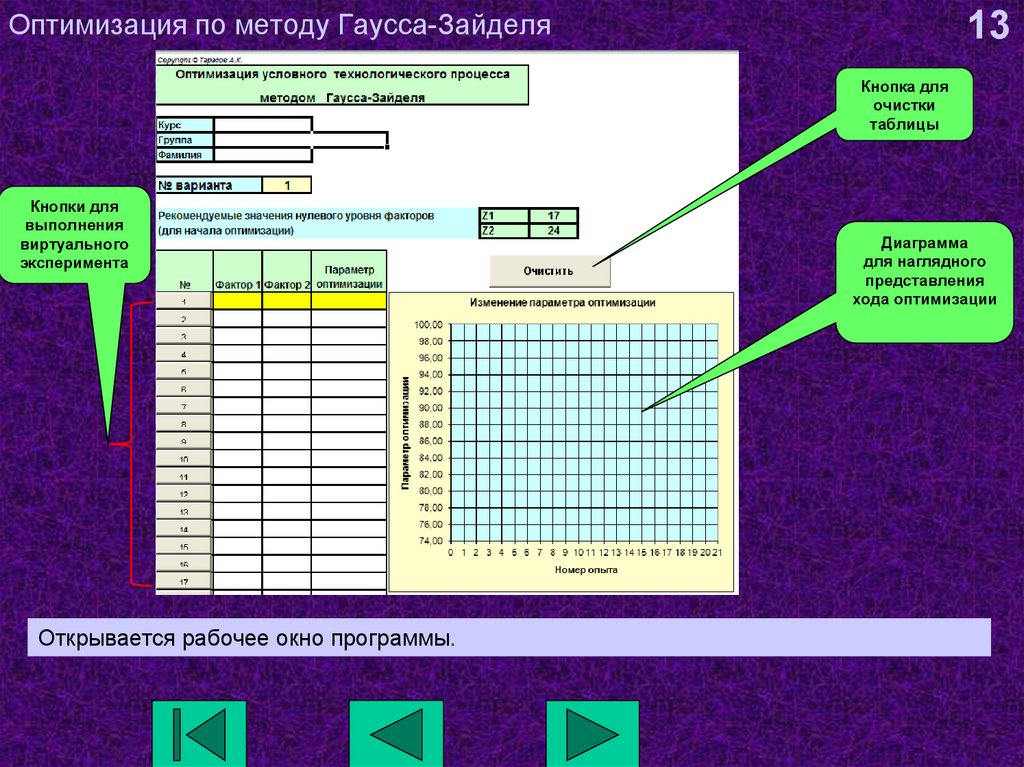
13. Оптимизация по методу Гаусса-Зайделя

13
Кнопка для
очистки
таблицы
Кнопки для
выполнения
виртуального
эксперимента
Открывается рабочее окно программы.
Диаграмма
для наглядного
представления
хода оптимизации

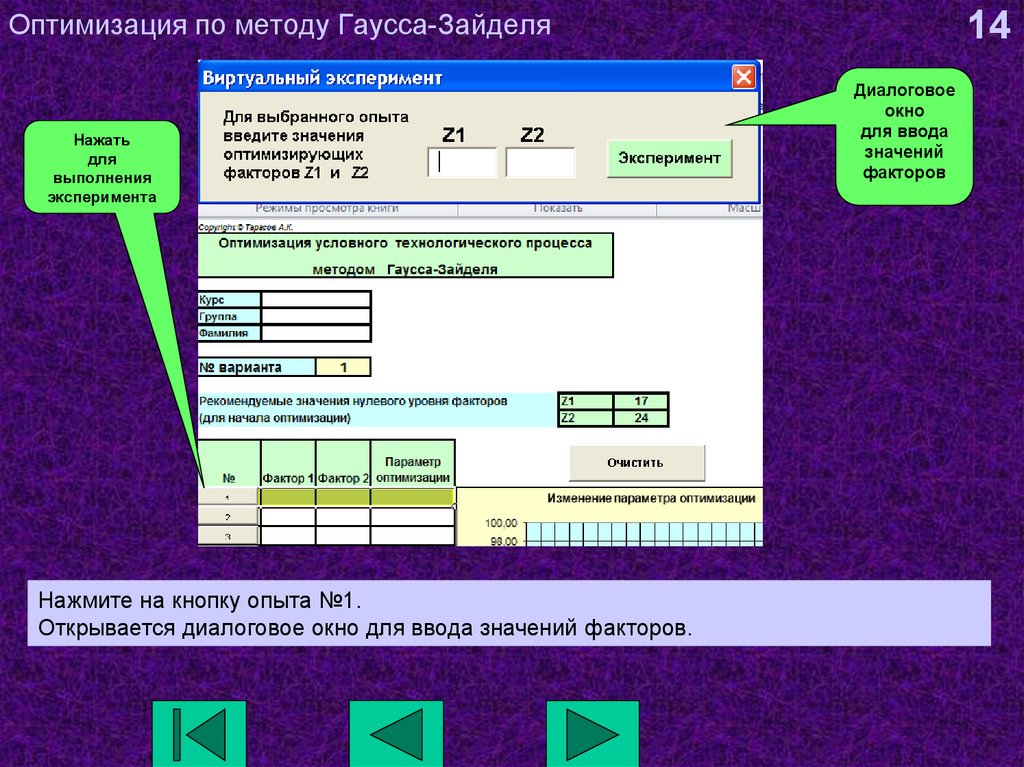
14. Оптимизация по методу Гаусса-Зайделя

Нажать
для
выполнения
эксперимента
Нажмите на кнопку опыта №1.
Открывается диалоговое окно для ввода значений факторов.
14
Диалоговое
окно
для ввода
значений
факторов

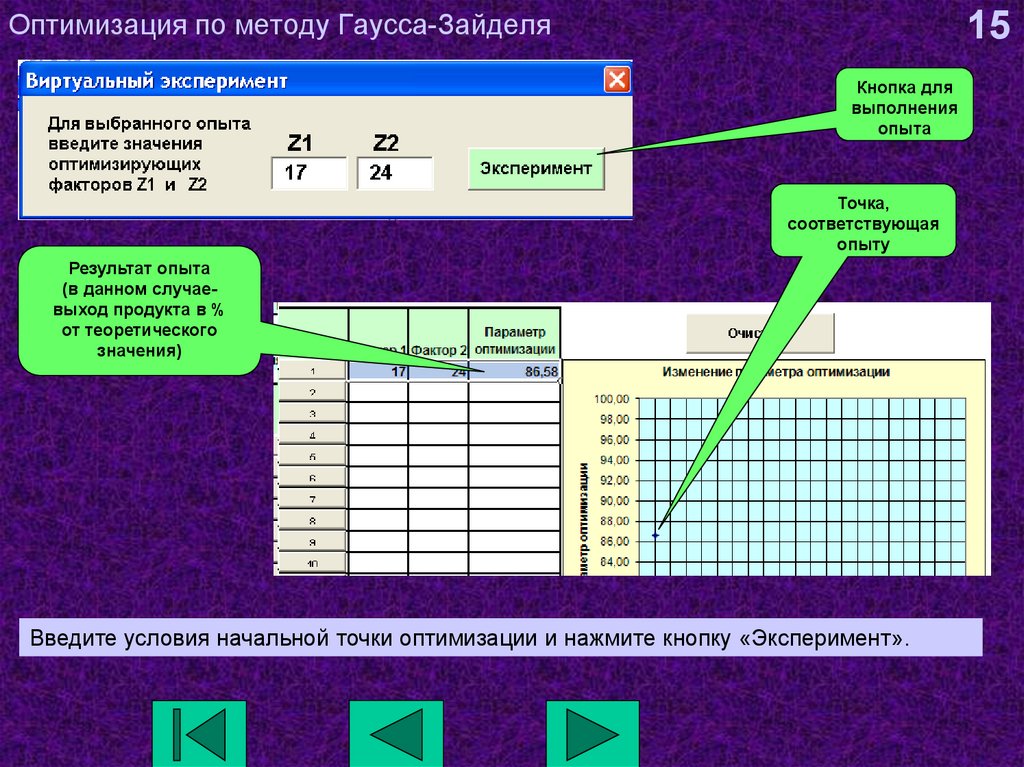
15. Оптимизация по методу Гаусса-Зайделя

15
Кнопка для
выполнения
опыта
Точка,
соответствующая
опыту
Результат опыта
(в данном случаевыход продукта в %
от теоретического
значения)
Введите условия начальной точки оптимизации и нажмите кнопку «Эксперимент».

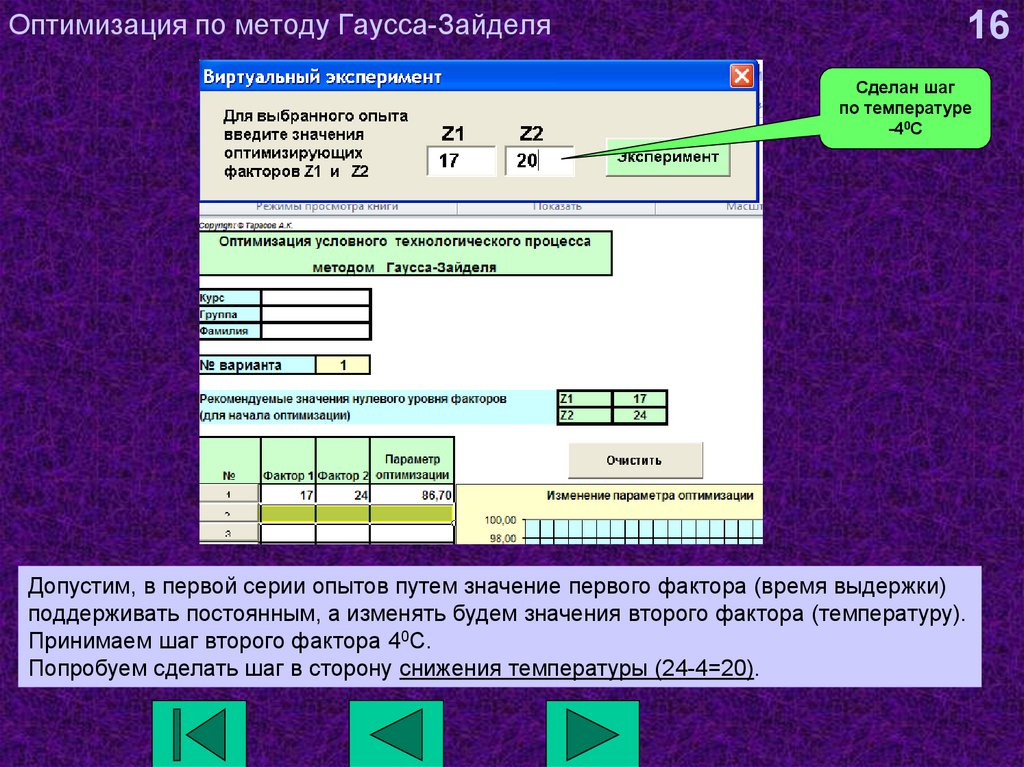
16. Оптимизация по методу Гаусса-Зайделя

16
Сделан шаг
по температуре
-40С
Допустим, в первой серии опытов путем значение первого фактора (время выдержки)
поддерживать постоянным, а изменять будем значения второго фактора (температуру).
Принимаем шаг второго фактора 40С.
Попробуем сделать шаг в сторону снижения температуры (24-4=20).

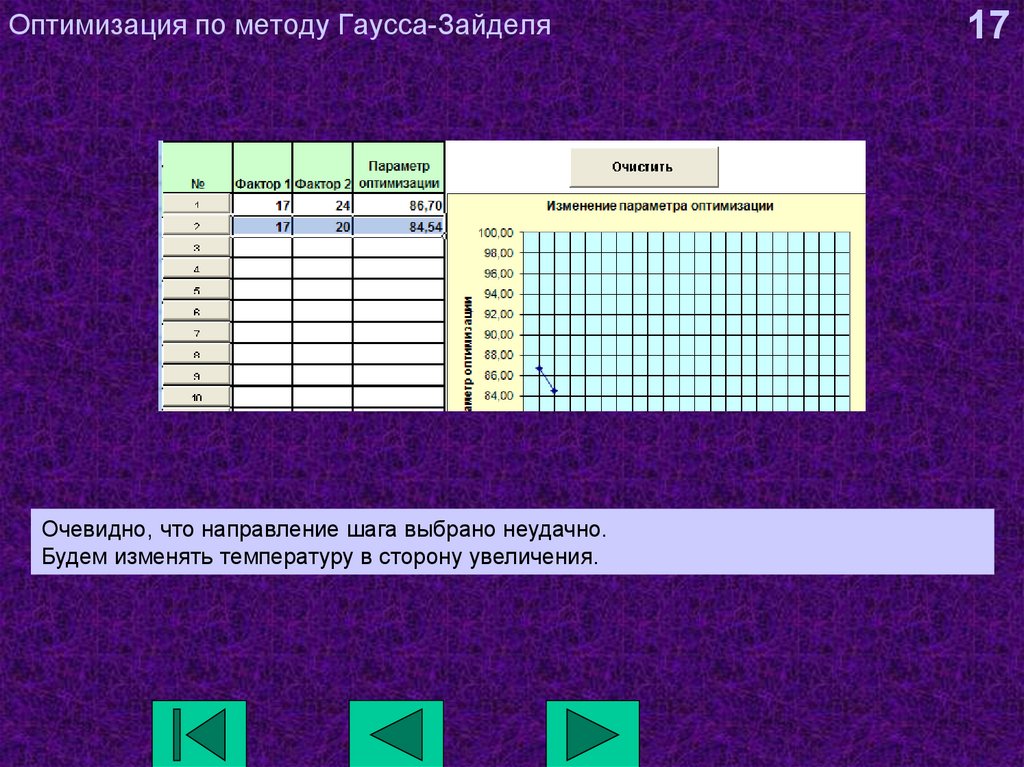
17. Оптимизация по методу Гаусса-Зайделя

Очевидно, что направление шага выбрано неудачно.
Будем изменять температуру в сторону увеличения.
17

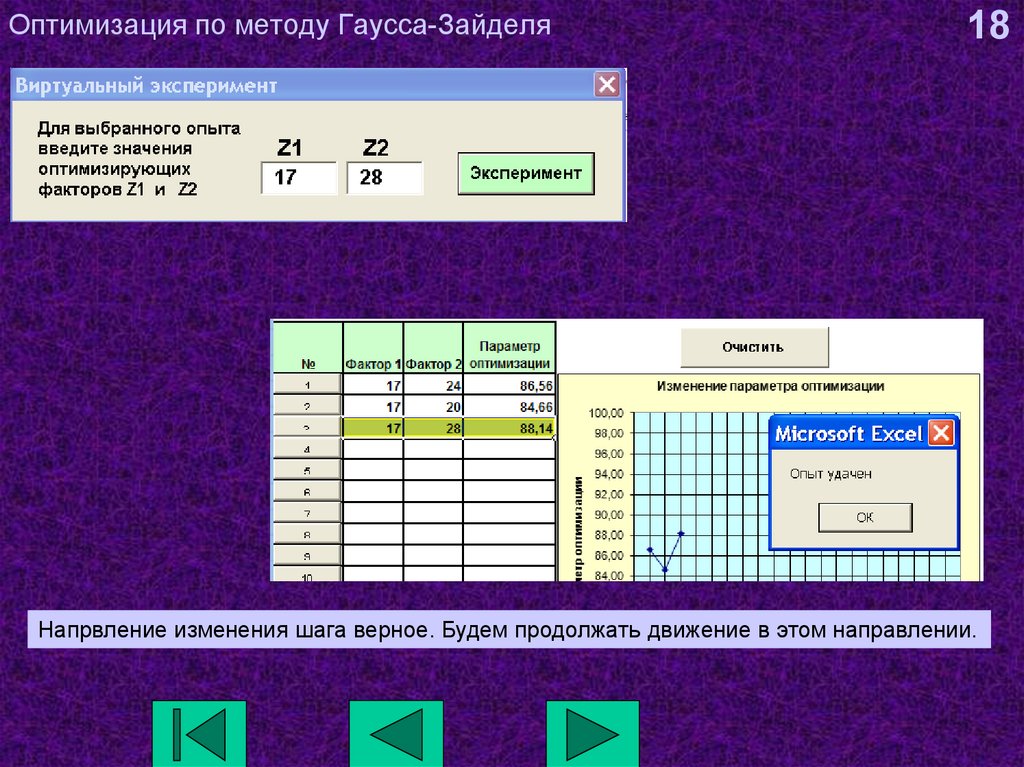
18. Оптимизация по методу Гаусса-Зайделя

18
Напрвление изменения шага верное. Будем продолжать движение в этом направлении.

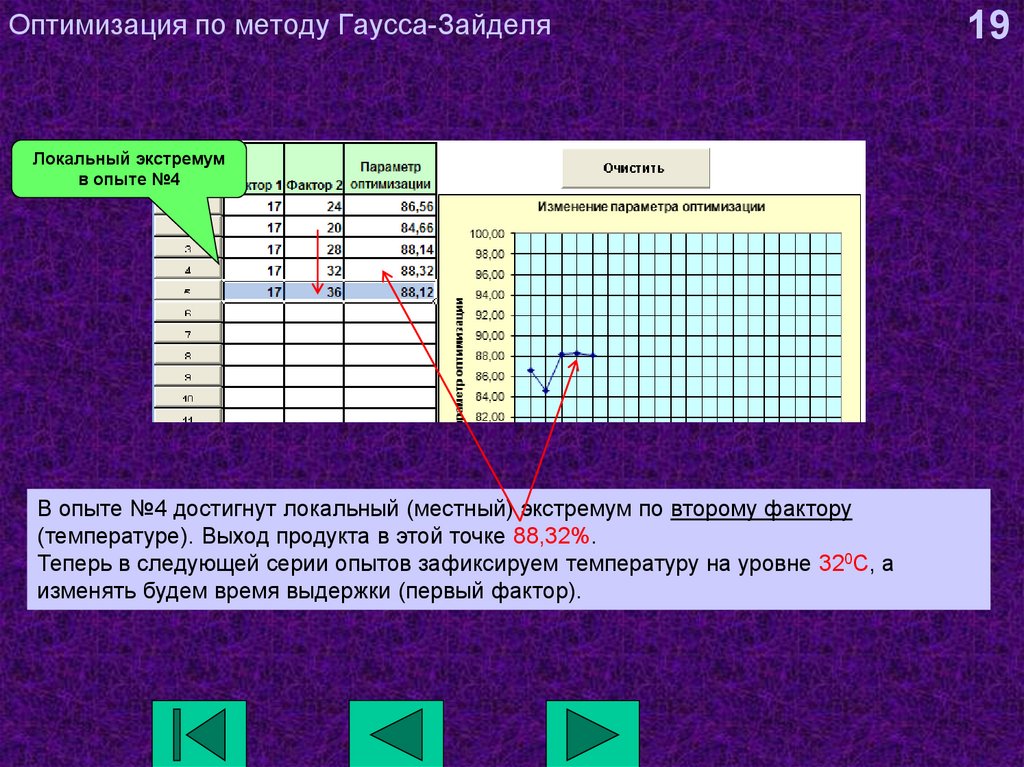
19. Оптимизация по методу Гаусса-Зайделя

Локальный экстремум
в опыте №4
В опыте №4 достигнут локальный (местный) экстремум по второму фактору
(температуре). Выход продукта в этой точке 88,32%.
Теперь в следующей серии опытов зафиксируем температуру на уровне 320С, а
изменять будем время выдержки (первый фактор).
19

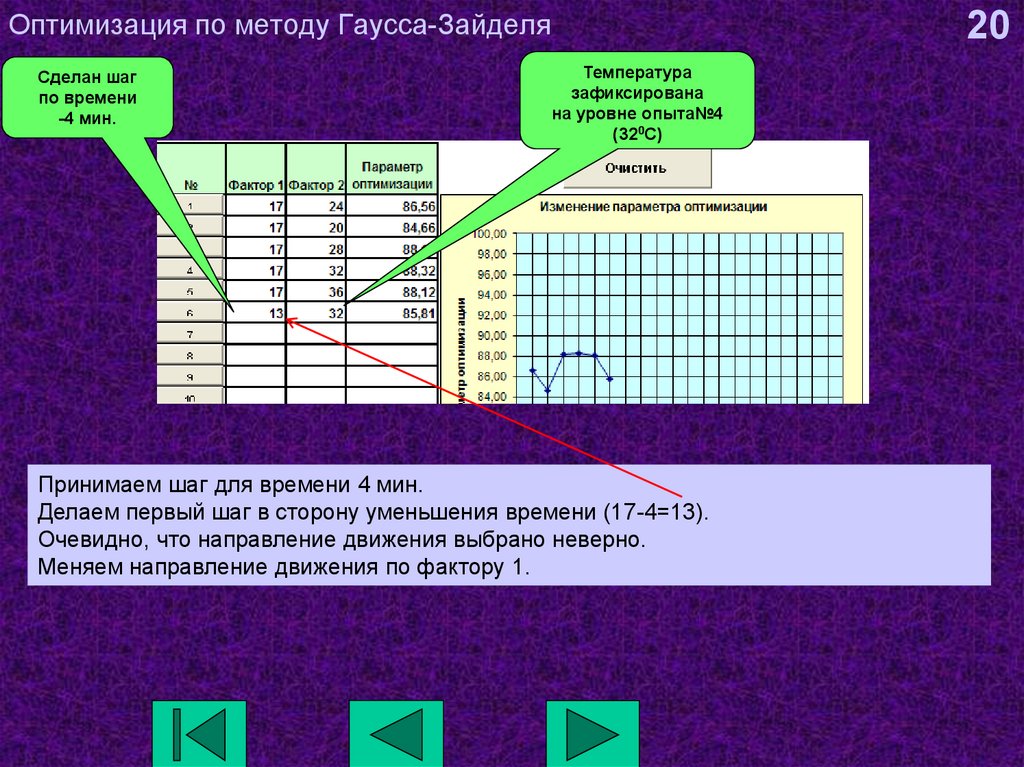
20. Оптимизация по методу Гаусса-Зайделя

Сделан шаг
по времени
-4 мин.
20
Температура
зафиксирована
на уровне опыта№4
(320С)
Принимаем шаг для времени 4 мин.
Делаем первый шаг в сторону уменьшения времени (17-4=13).
Очевидно, что направление движения выбрано неверно.
Меняем направление движения по фактору 1.

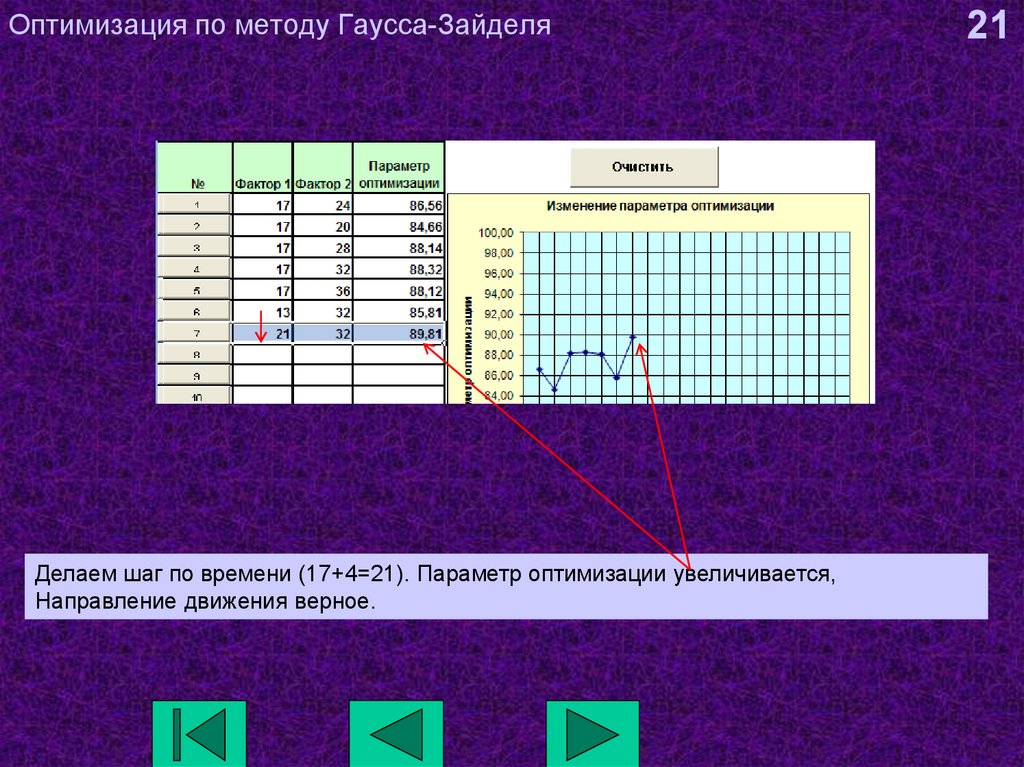
21. Оптимизация по методу Гаусса-Зайделя

Делаем шаг по времени (17+4=21). Параметр оптимизации увеличивается,
Направление движения верное.
21

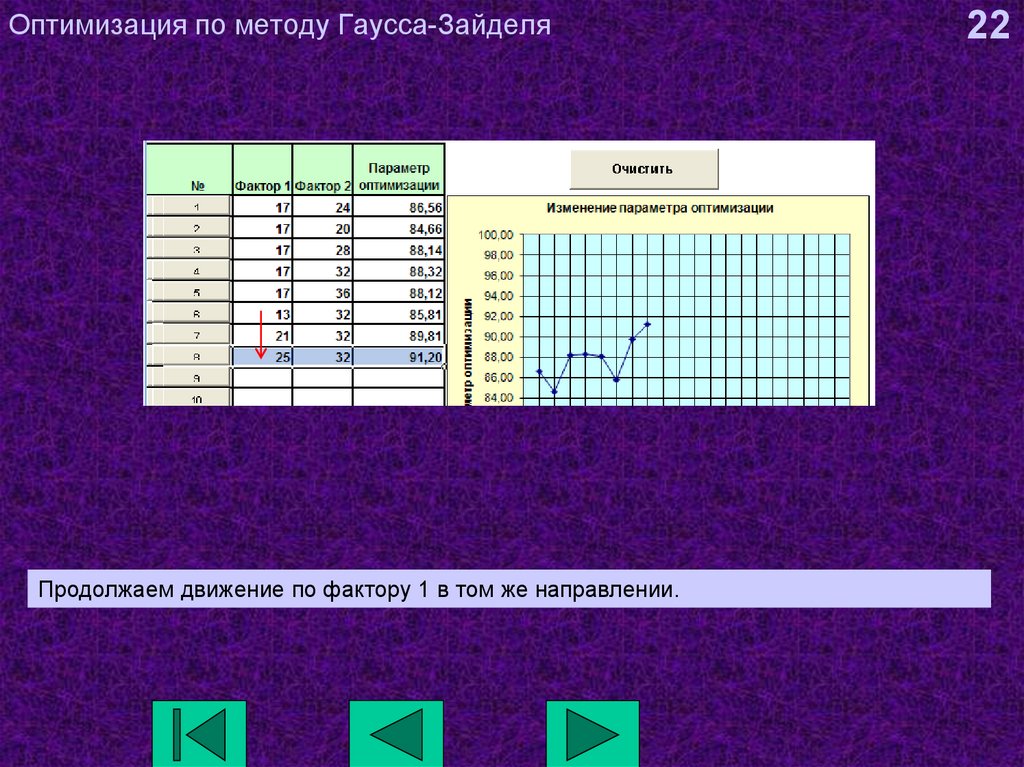
22. Оптимизация по методу Гаусса-Зайделя

Продолжаем движение по фактору 1 в том же направлении.
22

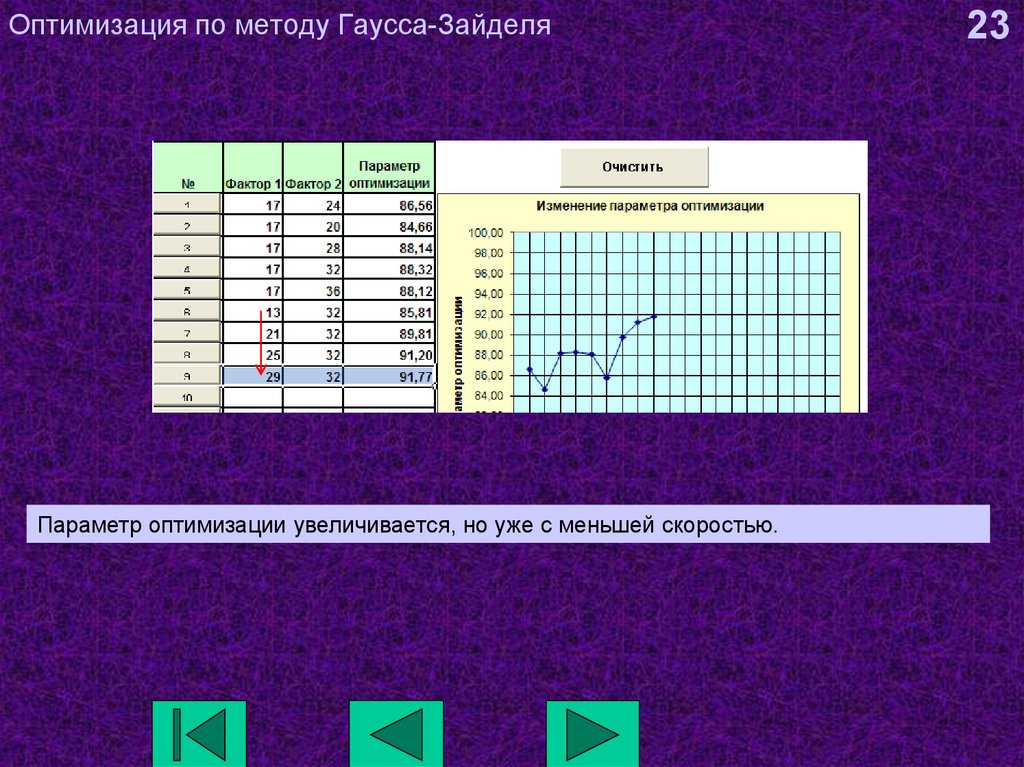
23. Оптимизация по методу Гаусса-Зайделя

Параметр оптимизации увеличивается, но уже с меньшей скоростью.
23

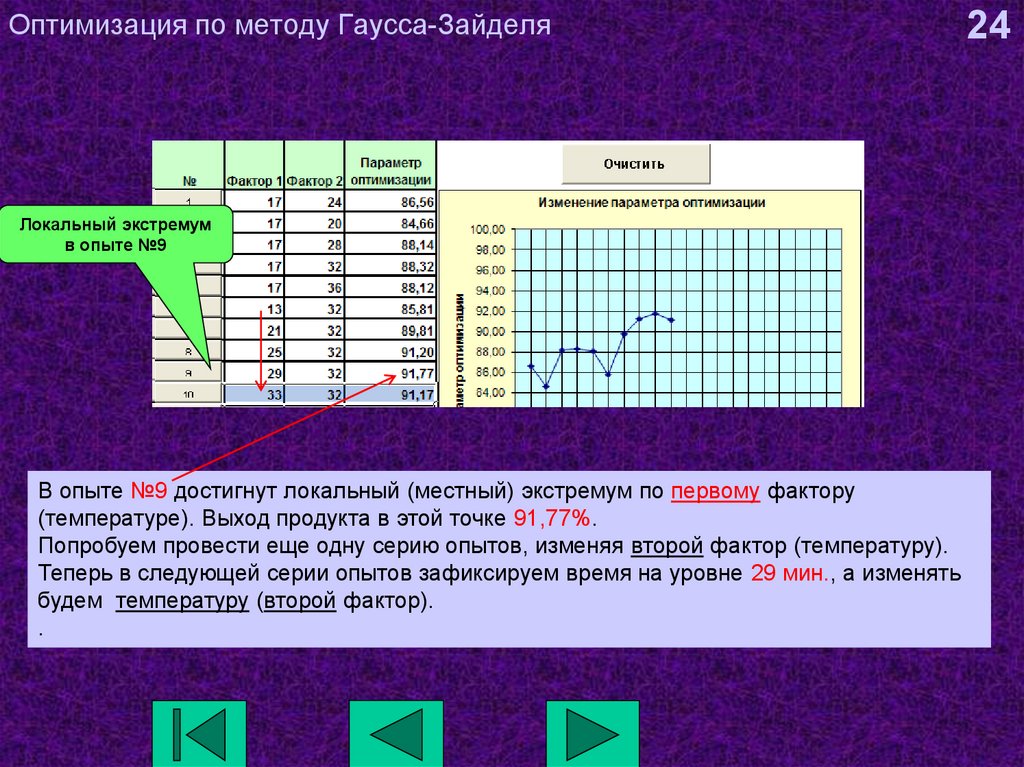
24. Оптимизация по методу Гаусса-Зайделя

Локальный экстремум
в опыте №9
В опыте №9 достигнут локальный (местный) экстремум по первому фактору
(температуре). Выход продукта в этой точке 91,77%.
Попробуем провести еще одну серию опытов, изменяя второй фактор (температуру).
Теперь в следующей серии опытов зафиксируем время на уровне 29 мин., а изменять
будем температуру (второй фактор).
.
24

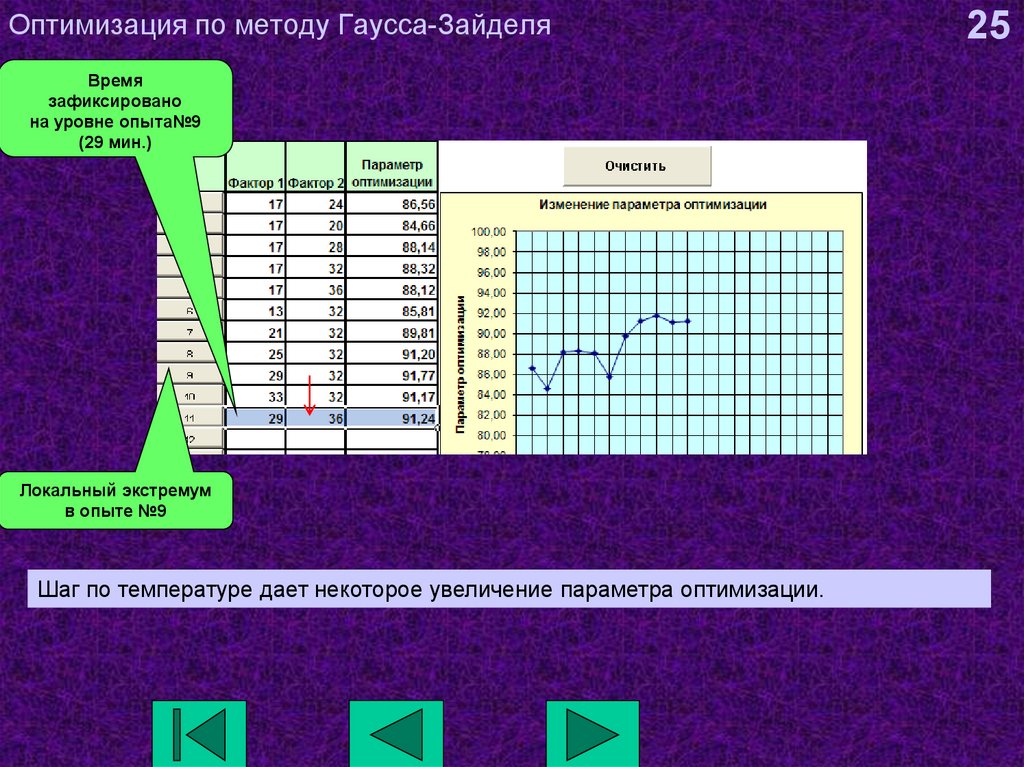
25. Оптимизация по методу Гаусса-Зайделя

Время
зафиксировано
на уровне опыта№9
(29 мин.)
Локальный экстремум
в опыте №9
Шаг по температуре дает некоторое увеличение параметра оптимизации.
25

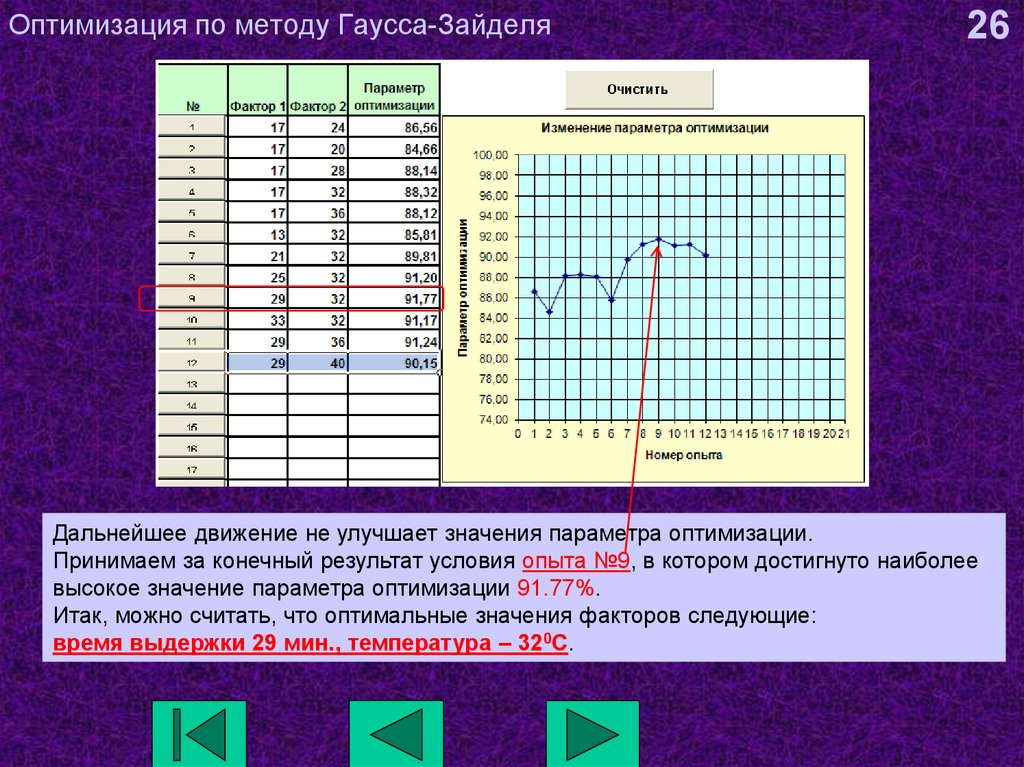
26. Оптимизация по методу Гаусса-Зайделя

26
Дальнейшее движение не улучшает значения параметра оптимизации.
Принимаем за конечный результат условия опыта №9, в котором достигнуто наиболее
высокое значение параметра оптимизации 91.77%.
Итак, можно считать, что оптимальные значения факторов следующие:
время выдержки 29 мин., температура – 320С.

27. Оптимизация по методу Гаусса-Зайделя

Контрольные вопросы
1 В чем сущность метода оптимизации по Гауссу-Зайделю?
2 В чем достоинства метода Гаусса-Зайделя?
3 Какие недостатки у метода Гаусса-Зайделя?
4 Что такое шаг при статистической оптимизации?
5 Какие критерии применяют при выборе шага?
27

28. Оптимизация по методу Гаусса-Зайделя

Данное упражнение выполняется в среде Excel.
Откройте файл-шаблон упражнения с помощью приведенной ниже гиперссылки.
Ссылка для файла-шаблона данного упражнения
28

29.

29
Упражнение 3.
Оптимизация симплекс-методом

30. Оптимизация симплекс-методом

В данном упражнении нужно работать с программой, имитирующей реальный
эксперимент и выполнять графические построения.
Изучите методику и технику выполнения данного упражнения.
В конце этого раздела будет ссылка на запуск программы-имитатора,
30

31. Оптимизация симплекс-методом

31
При запуске программы-имитатора появляется сначала появляется ее титульный кадр.

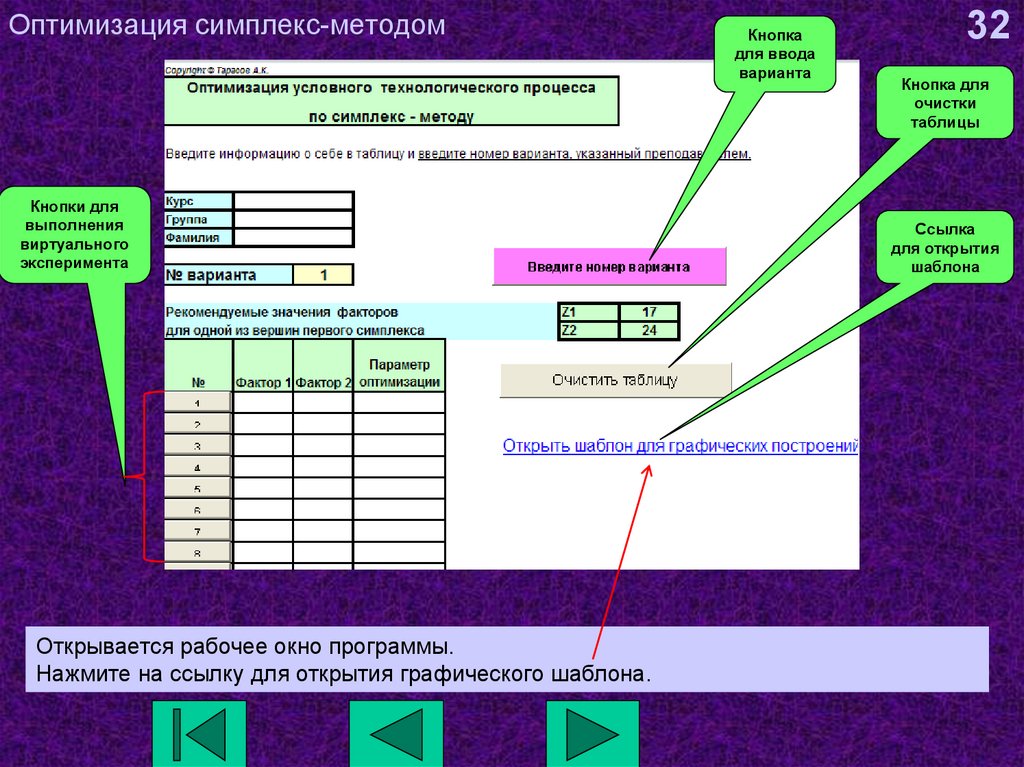
32. Оптимизация симплекс-методом

Кнопки для
выполнения
виртуального
эксперимента
Открывается рабочее окно программы.
Нажмите на ссылку для открытия графического шаблона.
Кнопка
для ввода
варианта
32
Кнопка для
очистки
таблицы
Ссылка
для открытия
шаблона

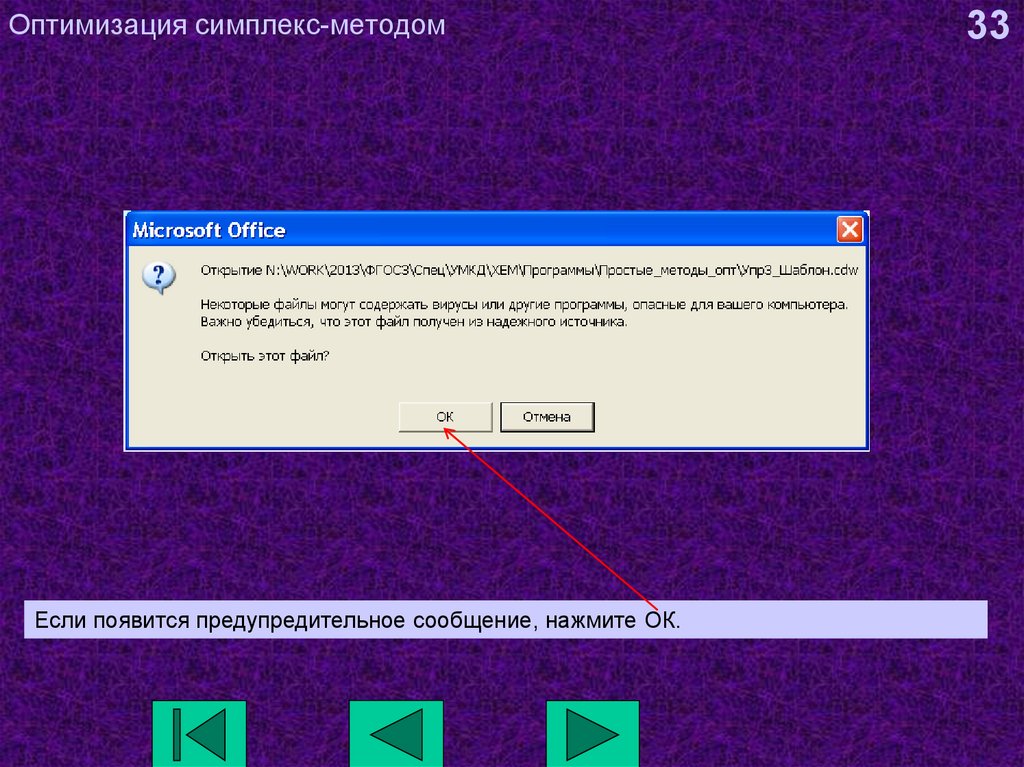
33. Оптимизация симплекс-методом

Если появится предупредительное сообщение, нажмите ОК.
33

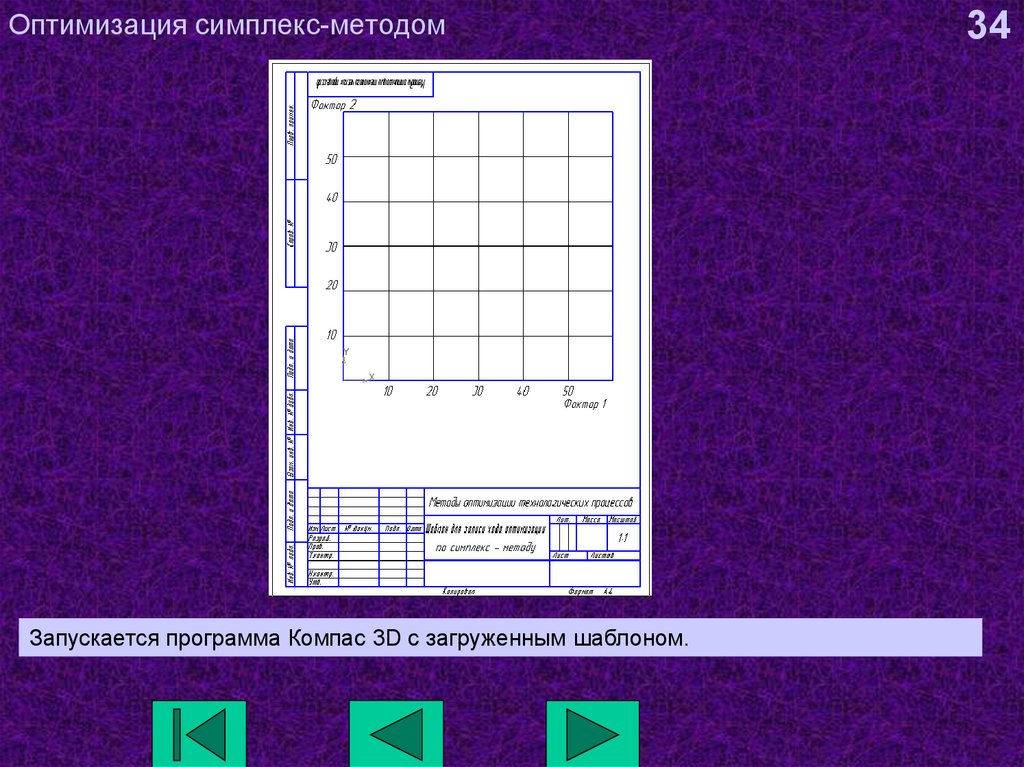
34. Оптимизация симплекс-методом

Запускается программа Компас 3D c загруженным шаблоном.
34

35. Оптимизация симплекс-методом

Не следует считать, что при оптимизации симплекс-методом
обязательно выполняются графические построения.
Есть методики с использованием вычисления координат точек
симплекса аналитическим методом.
Кроме того, графический способ планирования симплекс-метода
применим только для оптимизации по двум факторам.
Однако графический метод весьма нагляден для изучения данного
способа оптимизации.
35

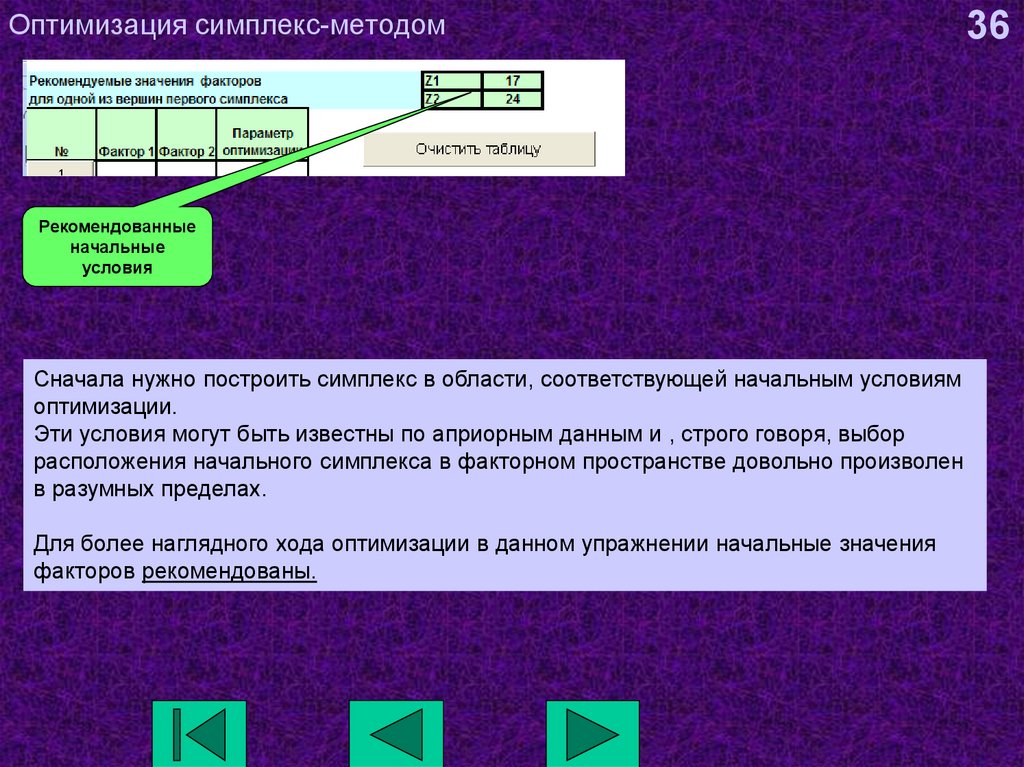
36. Оптимизация симплекс-методом

Рекомендованные
начальные
условия
Сначала нужно построить симплекс в области, соответствующей начальным условиям
оптимизации.
Эти условия могут быть известны по априорным данным и , строго говоря, выбор
расположения начального симплекса в факторном пространстве довольно произволен
в разумных пределах.
Для более наглядного хода оптимизации в данном упражнении начальные значения
факторов рекомендованы.
36

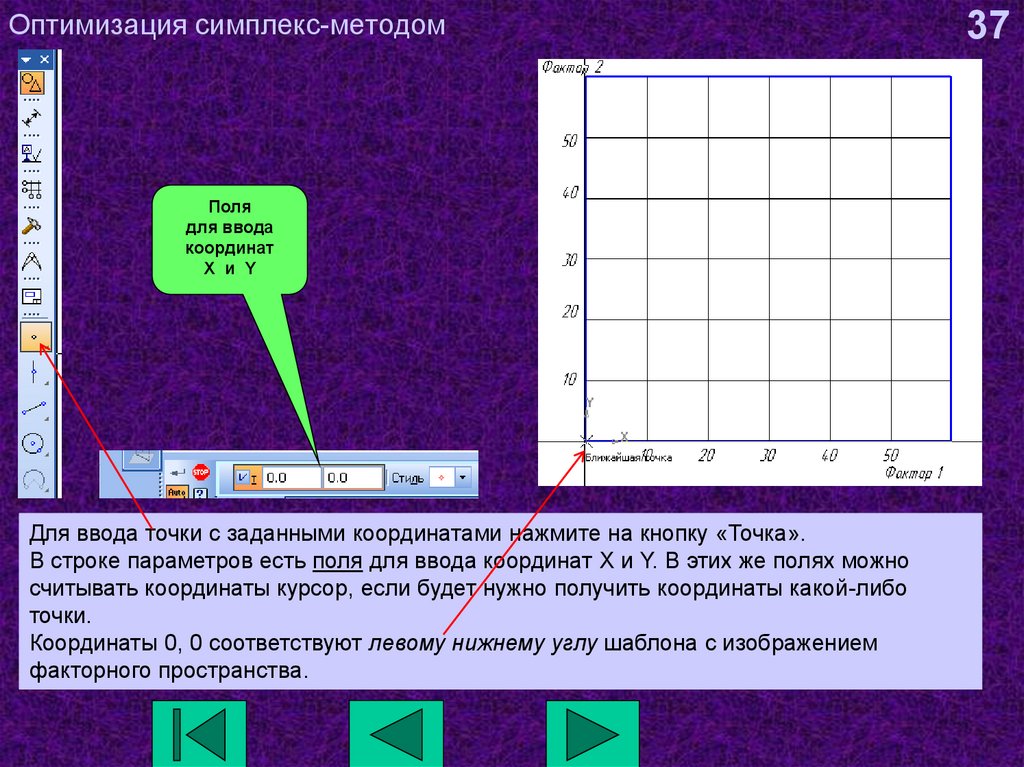
37. Оптимизация симплекс-методом

Поля
для ввода
координат
X и Y
Для ввода точки с заданными координатами нажмите на кнопку «Точка».
В строке параметров есть поля для ввода координат X и Y. В этих же полях можно
считывать координаты курсор, если будет нужно получить координаты какой-либо
точки.
Координаты 0, 0 соответствуют левому нижнему углу шаблона с изображением
факторного пространства.
37

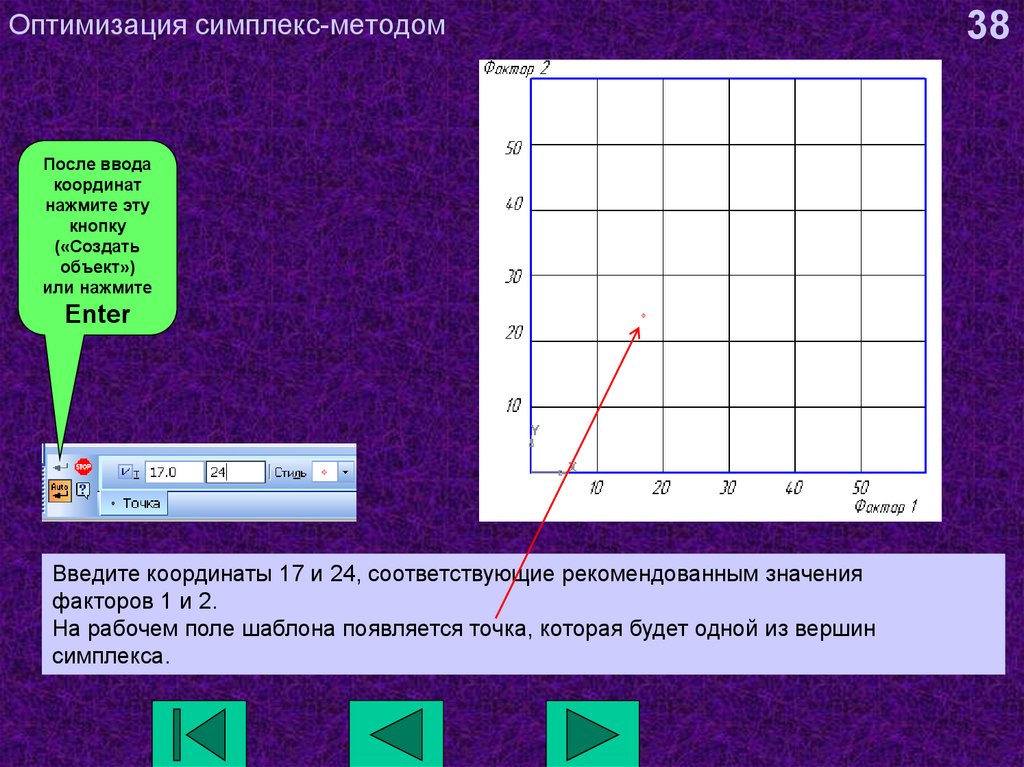
38. Оптимизация симплекс-методом

После ввода
координат
нажмите эту
кнопку
(«Создать
объект»)
или нажмите
Enter
Введите координаты 17 и 24, соответствующие рекомендованным значения
факторов 1 и 2.
На рабочем поле шаблона появляется точка, которая будет одной из вершин
симплекса.
38

39. Оптимизация симплекс-методом

Увеличьте изображение на экране.
39

40. Оптимизация симплекс-методом

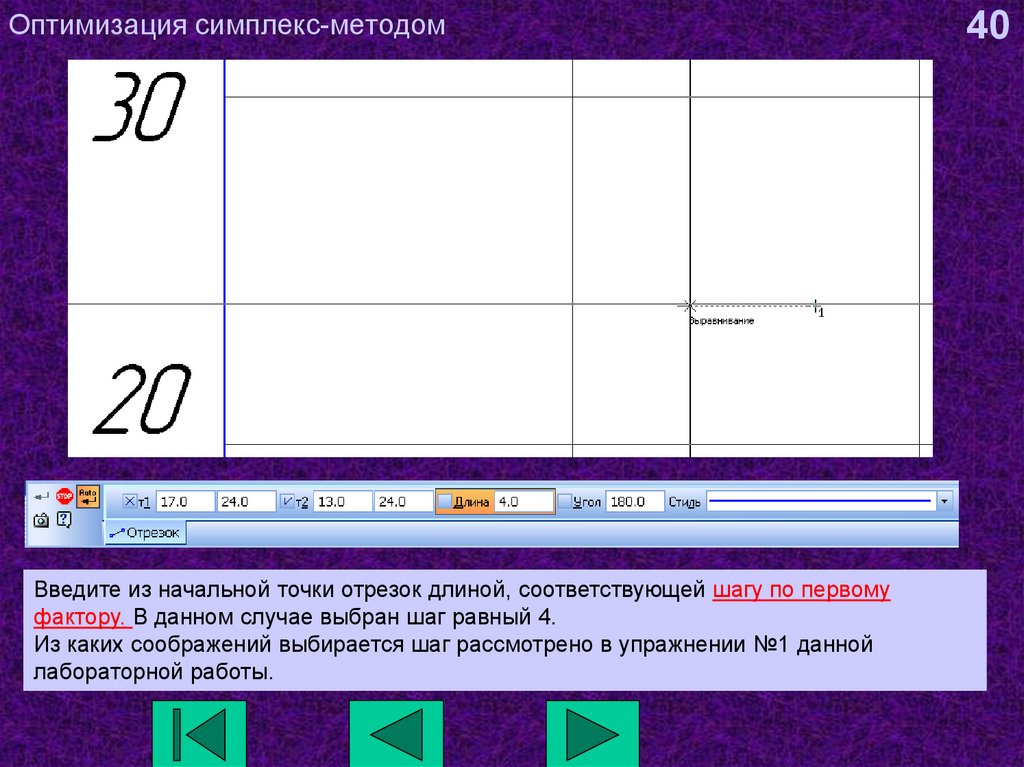
Введите из начальной точки отрезок длиной, соответствующей шагу по первому
фактору. В данном случае выбран шаг равный 4.
Из каких соображений выбирается шаг рассмотрено в упражнении №1 данной
лабораторной работы.
40

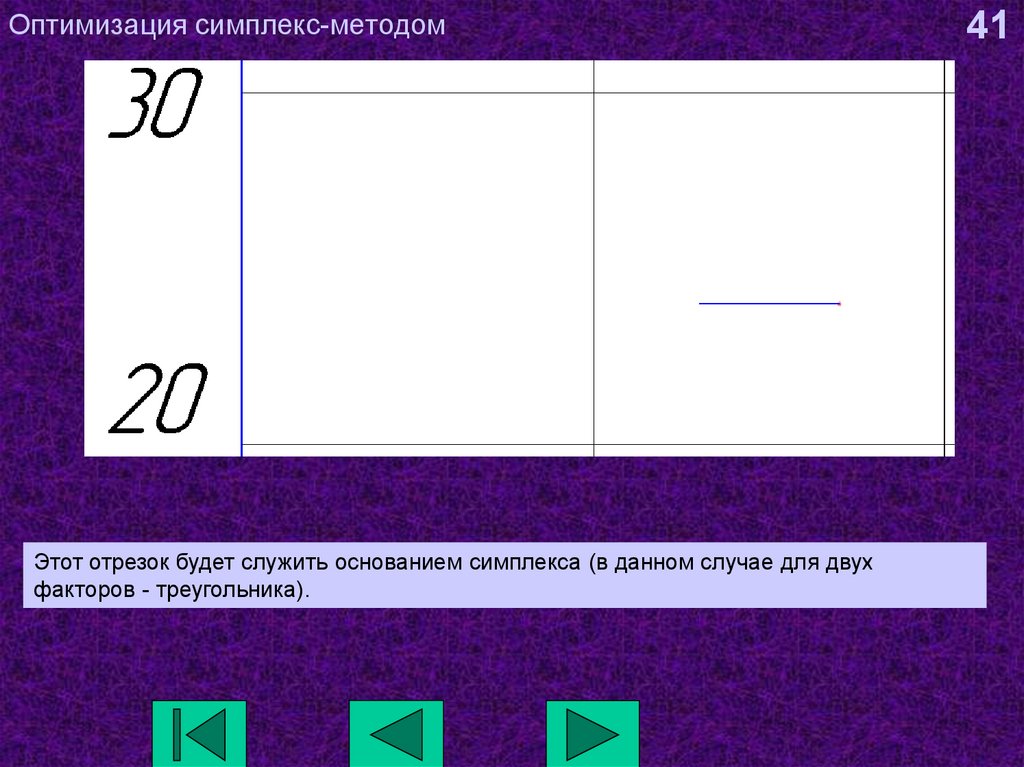
41. Оптимизация симплекс-методом

Этот отрезок будет служить основанием симплекса (в данном случае для двух
факторов - треугольника).
41

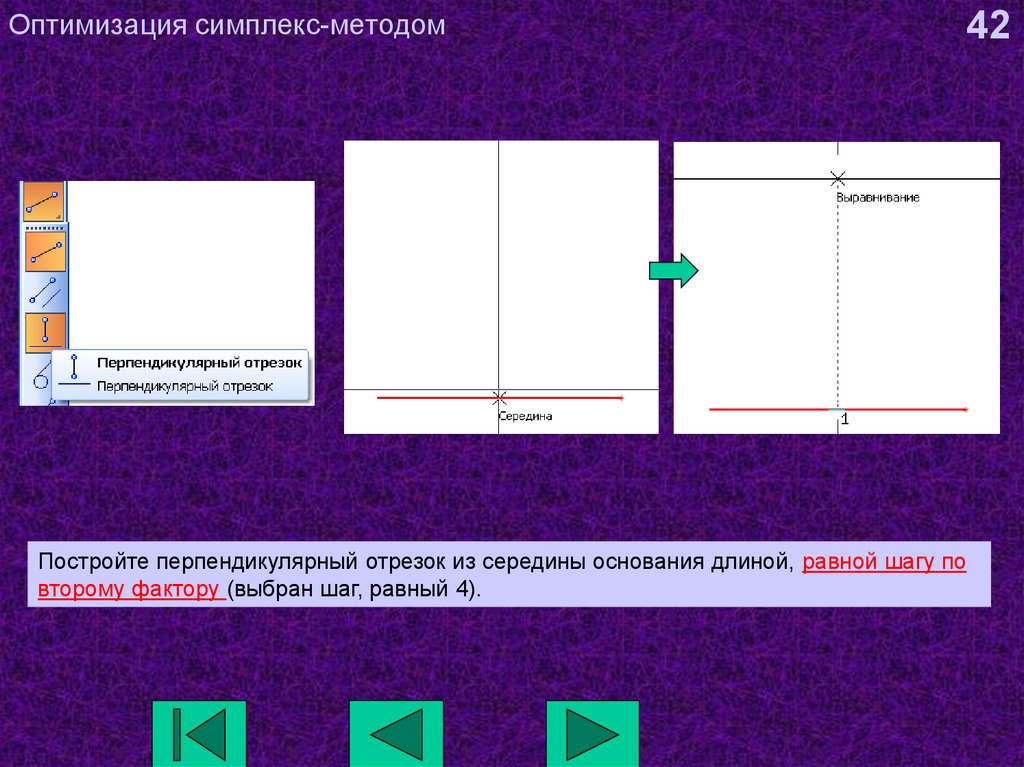
42. Оптимизация симплекс-методом

42
Постройте перпендикулярный отрезок из середины основания длиной, равной шагу по
второму фактору (выбран шаг, равный 4).

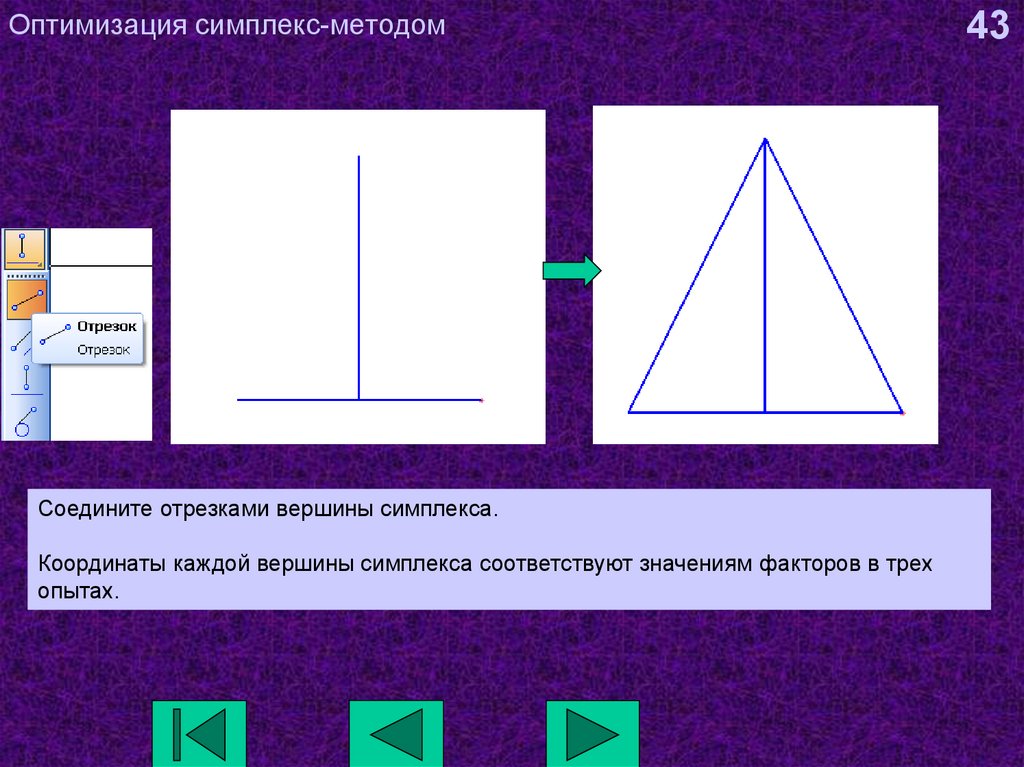
43. Оптимизация симплекс-методом

Соедините отрезками вершины симплекса.
Координаты каждой вершины симплекса соответствуют значениям факторов в трех
опытах.
43

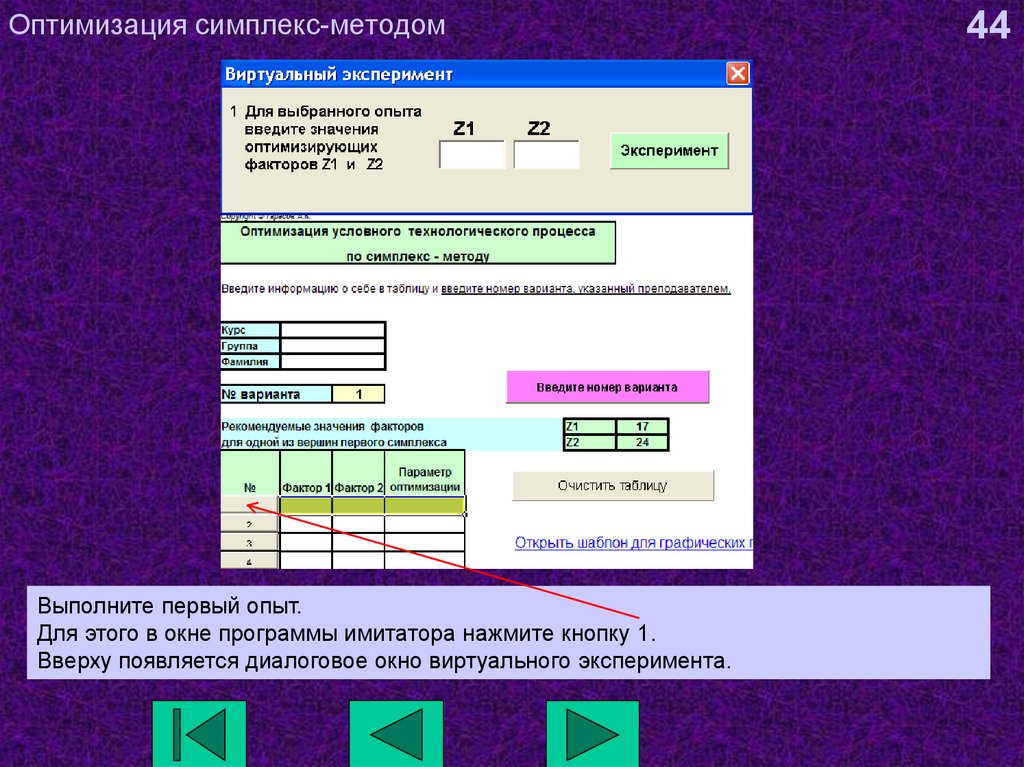
44. Оптимизация симплекс-методом

Выполните первый опыт.
Для этого в окне программы имитатора нажмите кнопку 1.
Вверху появляется диалоговое окно виртуального эксперимента.
44

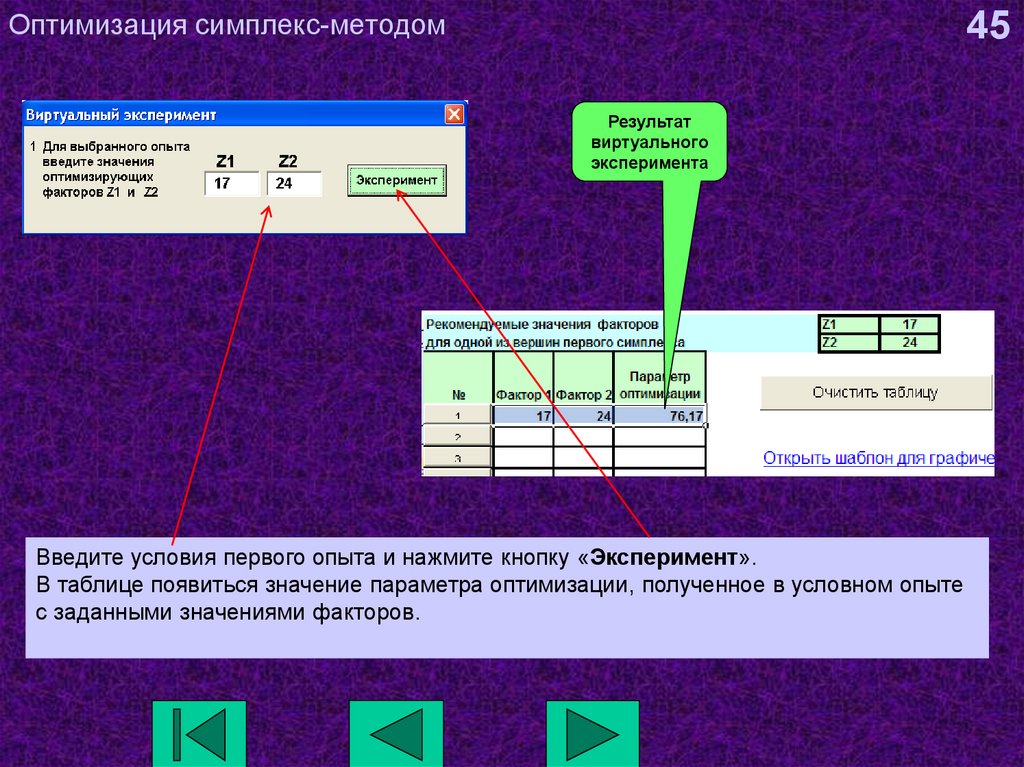
45. Оптимизация симплекс-методом

45
Результат
виртуального
эксперимента
Введите условия первого опыта и нажмите кнопку «Эксперимент».
В таблице появиться значение параметра оптимизации, полученное в условном опыте
с заданными значениями факторов.

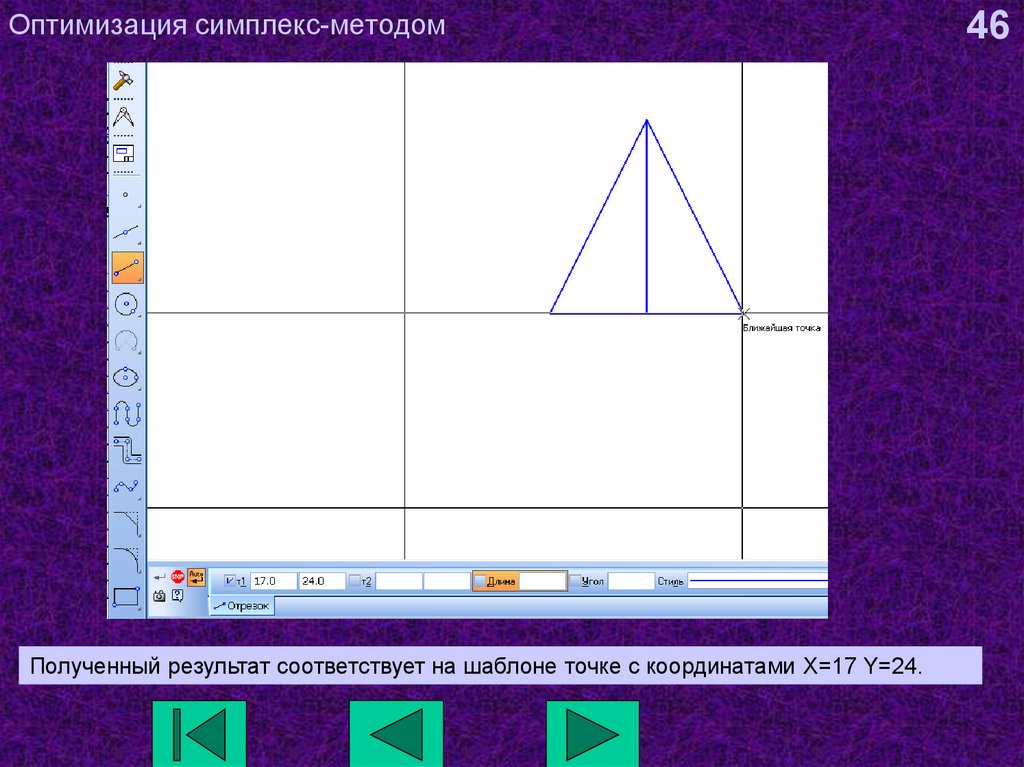
46. Оптимизация симплекс-методом

Полученный результат соответствует на шаблоне точке с координатами X=17 Y=24.
46

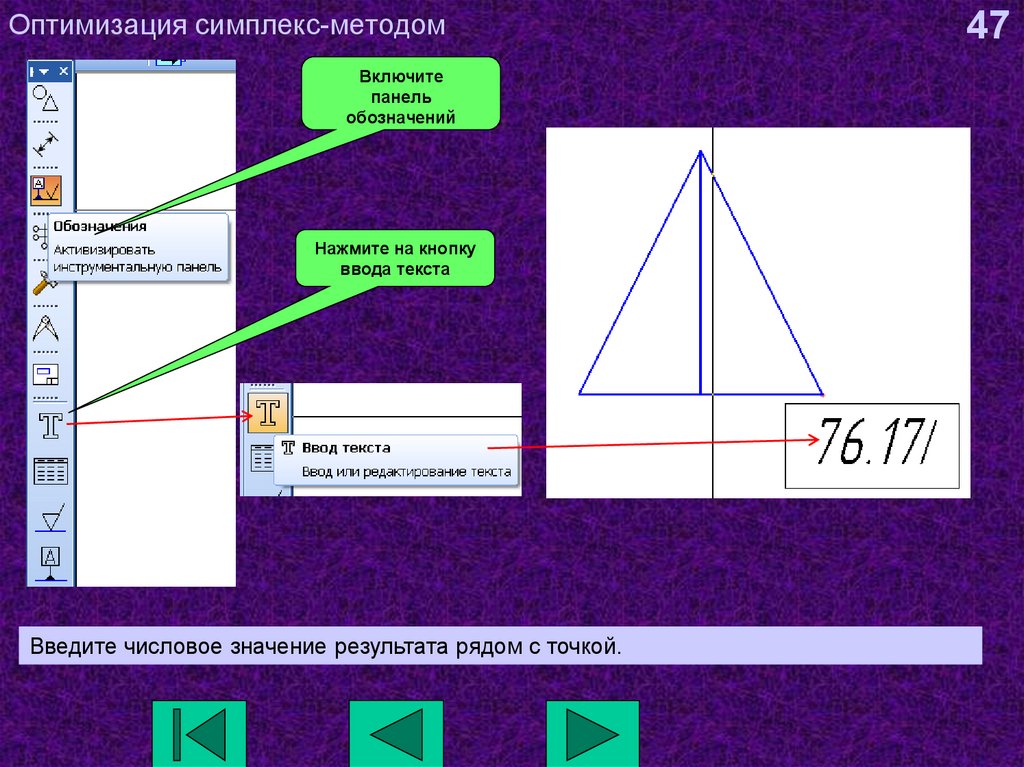
47. Оптимизация симплекс-методом

Включите
панель
обозначений
Нажмите на кнопку
ввода текста
Введите числовое значение результата рядом с точкой.
47

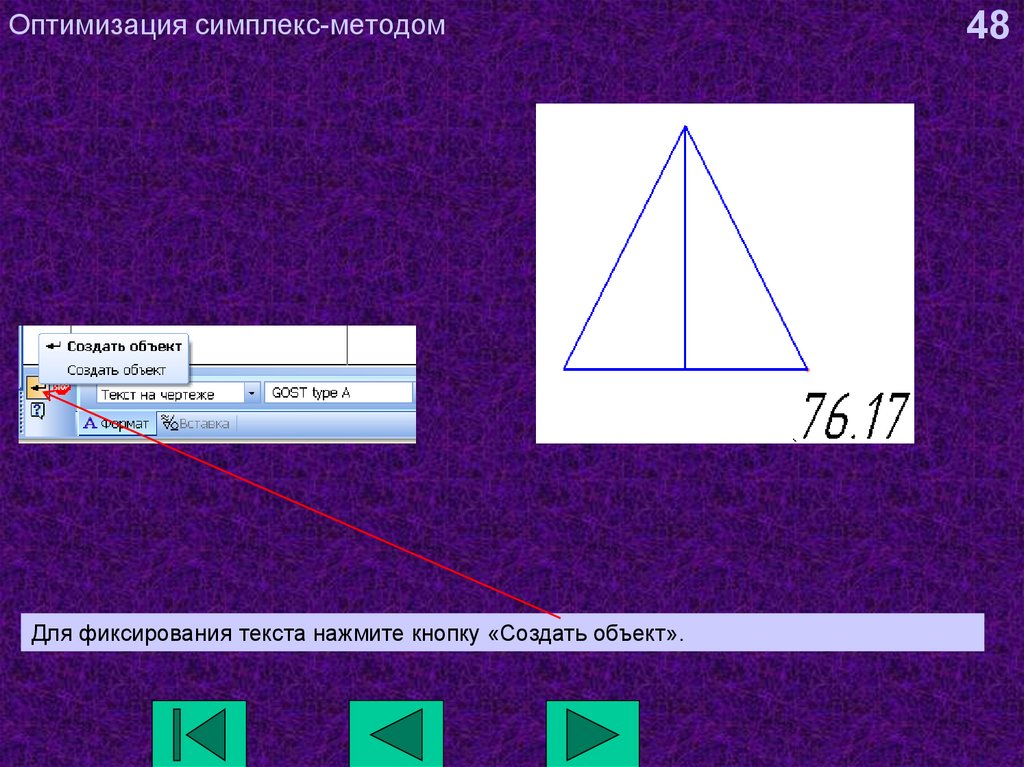
48. Оптимизация симплекс-методом

Для фиксирования текста нажмите кнопку «Создать объект».
48

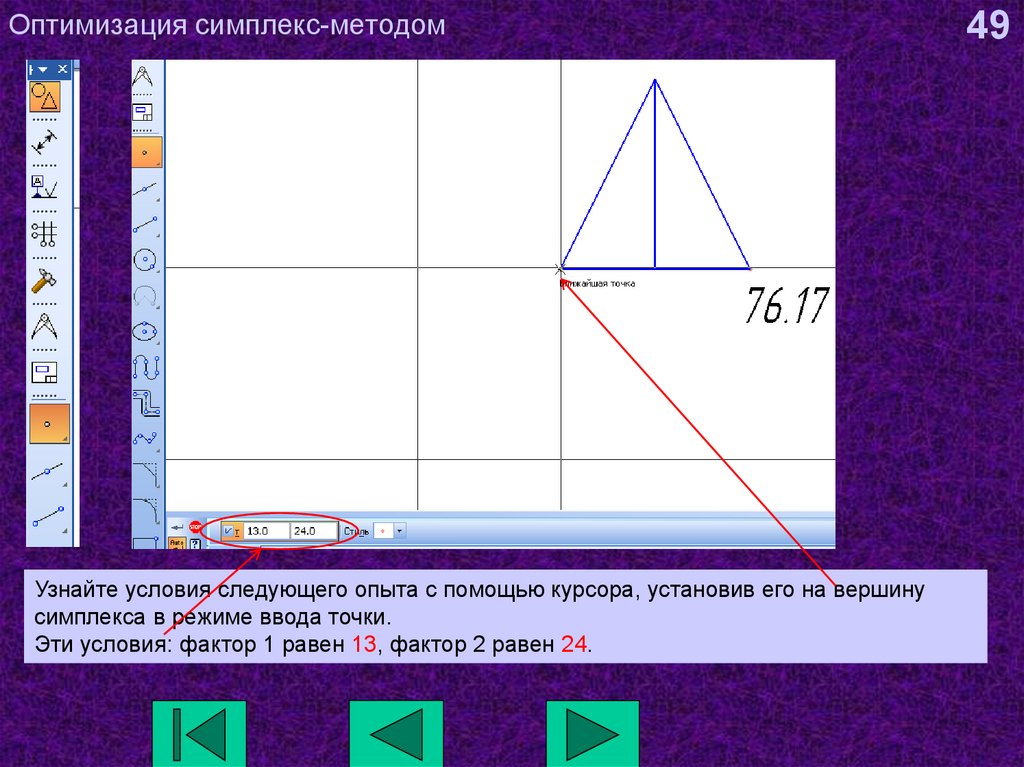
49. Оптимизация симплекс-методом

Узнайте условия следующего опыта с помощью курсора, установив его на вершину
симплекса в режиме ввода точки.
Эти условия: фактор 1 равен 13, фактор 2 равен 24.
49

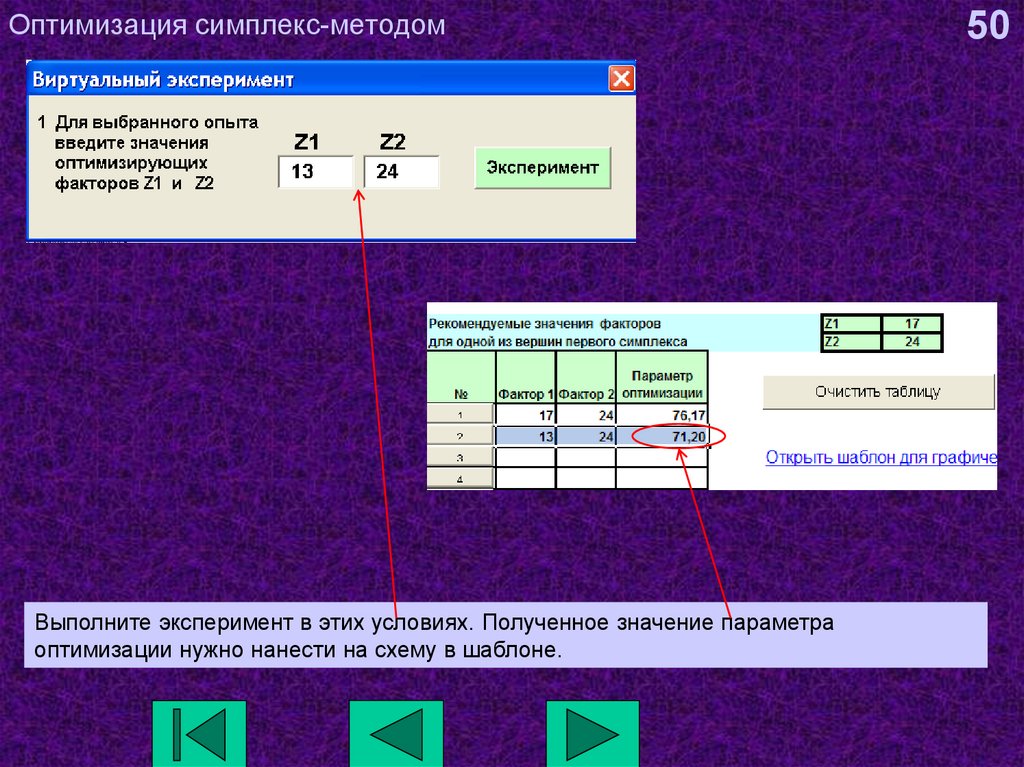
50. Оптимизация симплекс-методом

Выполните эксперимент в этих условиях. Полученное значение параметра
оптимизации нужно нанести на схему в шаблоне.
50

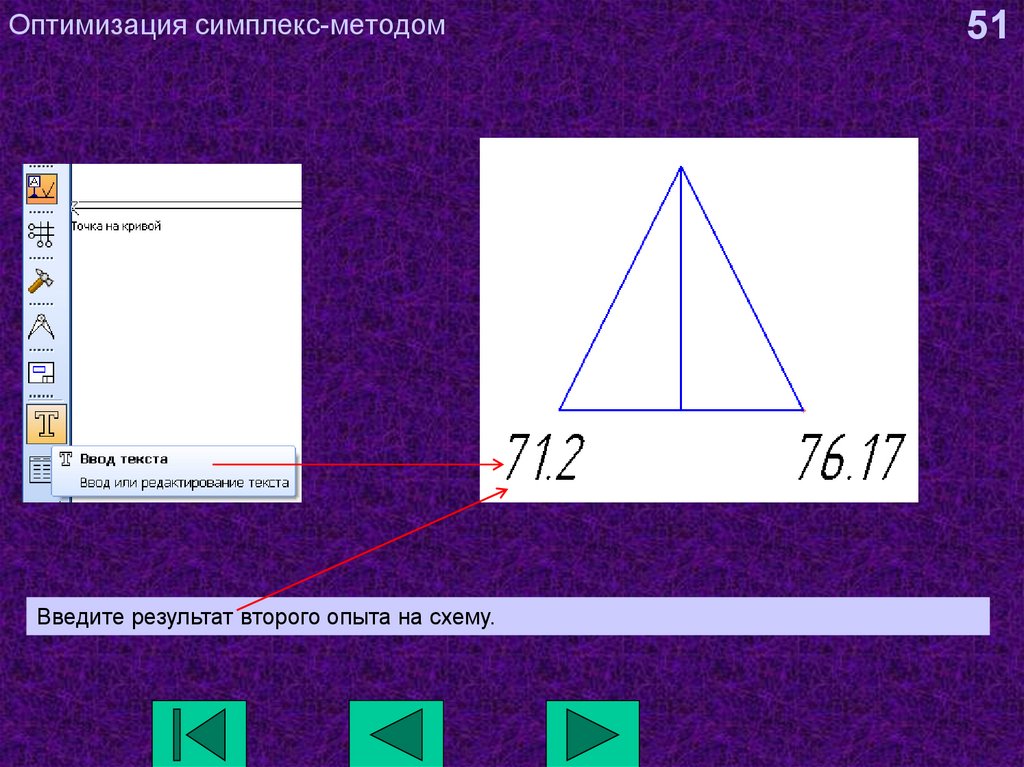
51. Оптимизация симплекс-методом

Введите результат второго опыта на схему.
51

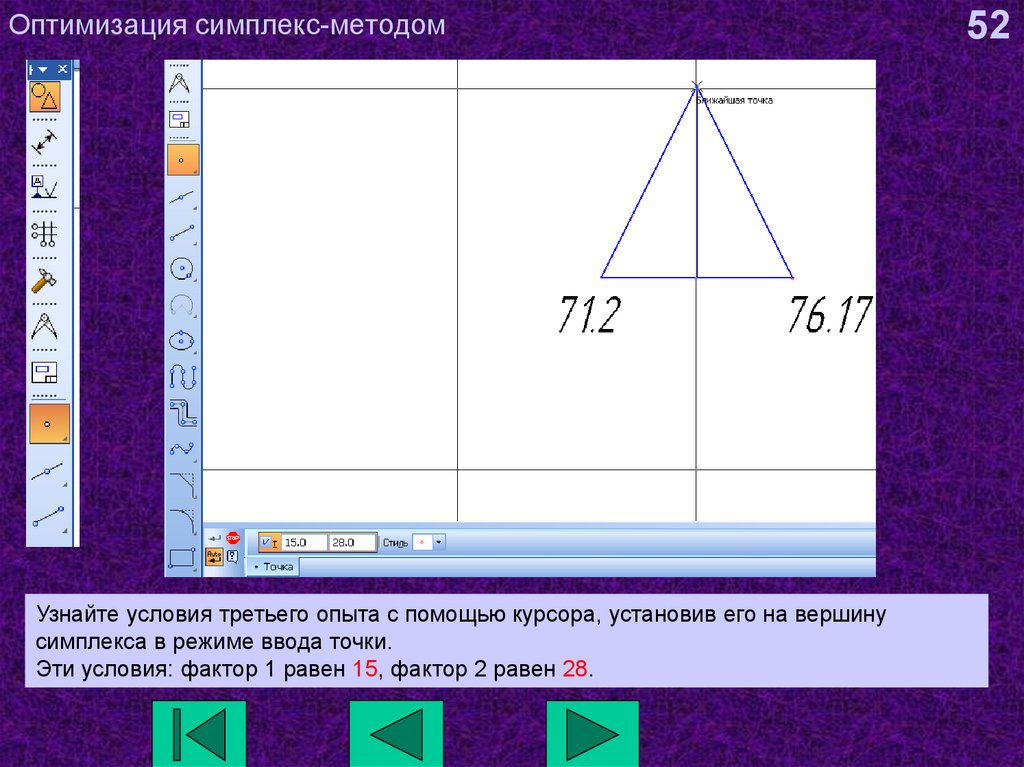
52. Оптимизация симплекс-методом

Узнайте условия третьего опыта с помощью курсора, установив его на вершину
симплекса в режиме ввода точки.
Эти условия: фактор 1 равен 15, фактор 2 равен 28.
52

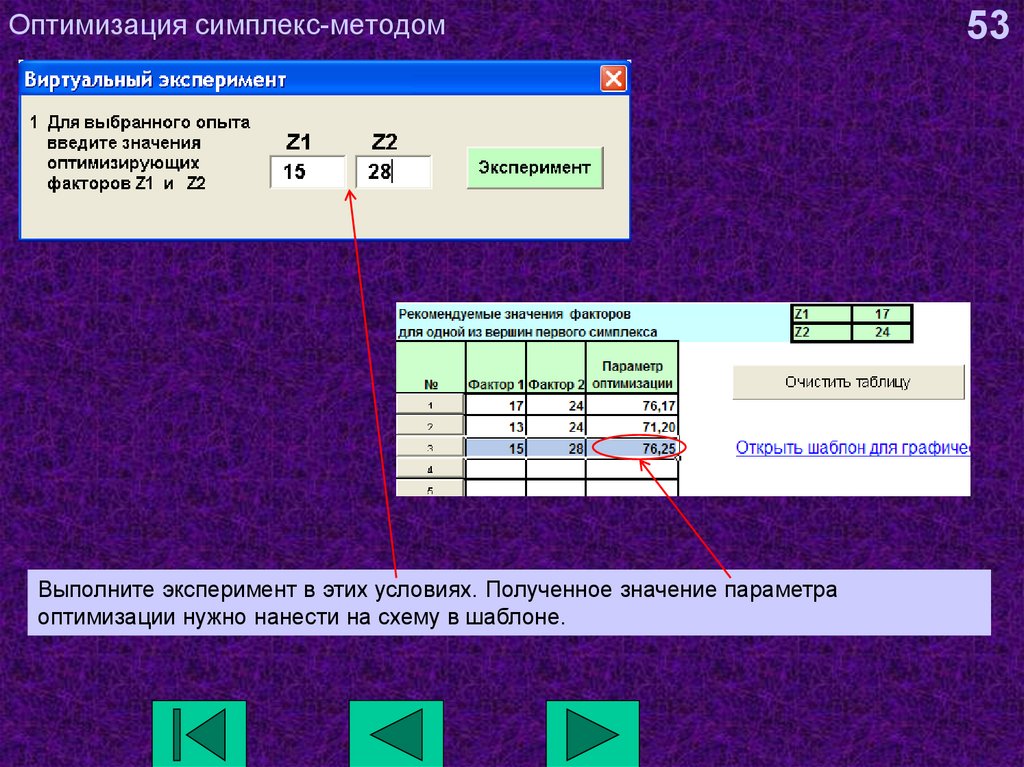
53. Оптимизация симплекс-методом

Выполните эксперимент в этих условиях. Полученное значение параметра
оптимизации нужно нанести на схему в шаблоне.
53

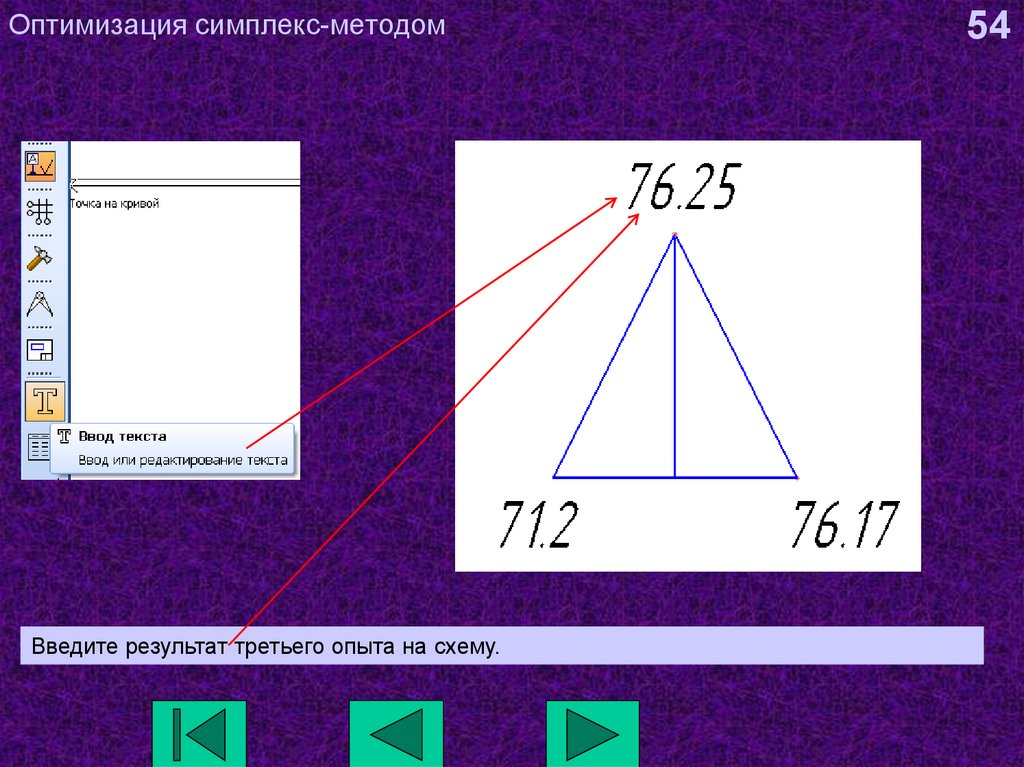
54. Оптимизация симплекс-методом

Введите результат третьего опыта на схему.
54

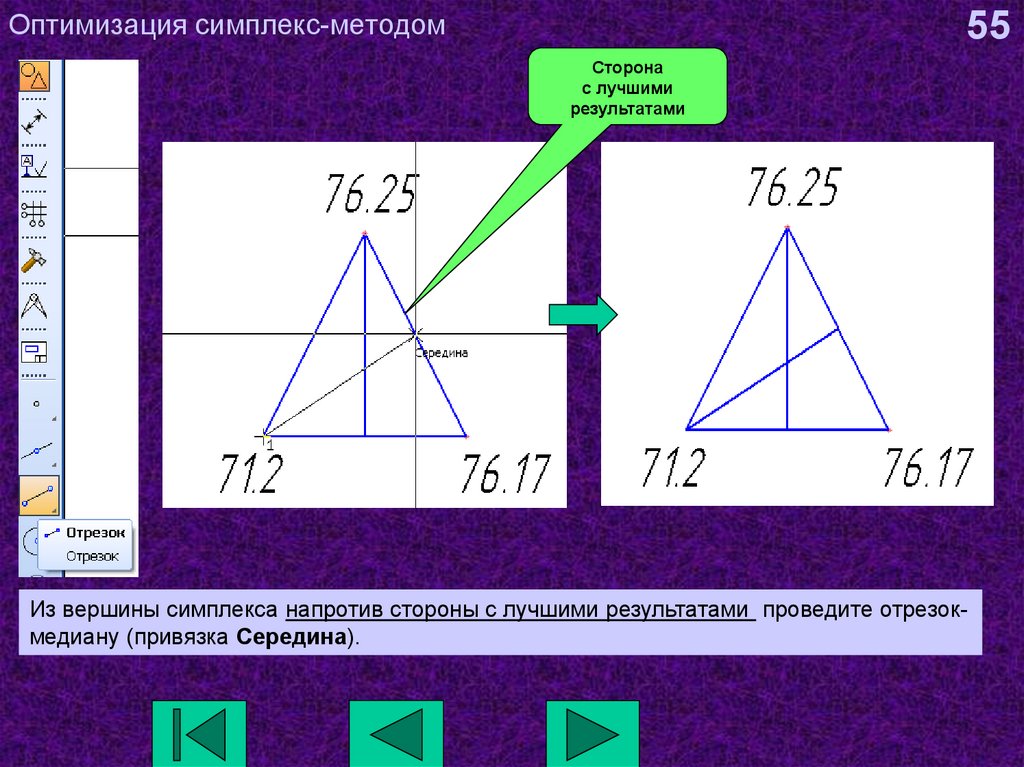
55. Оптимизация симплекс-методом

55
Сторона
с лучшими
результатами
Из вершины симплекса напротив стороны с лучшими результатами проведите отрезокмедиану (привязка Середина).

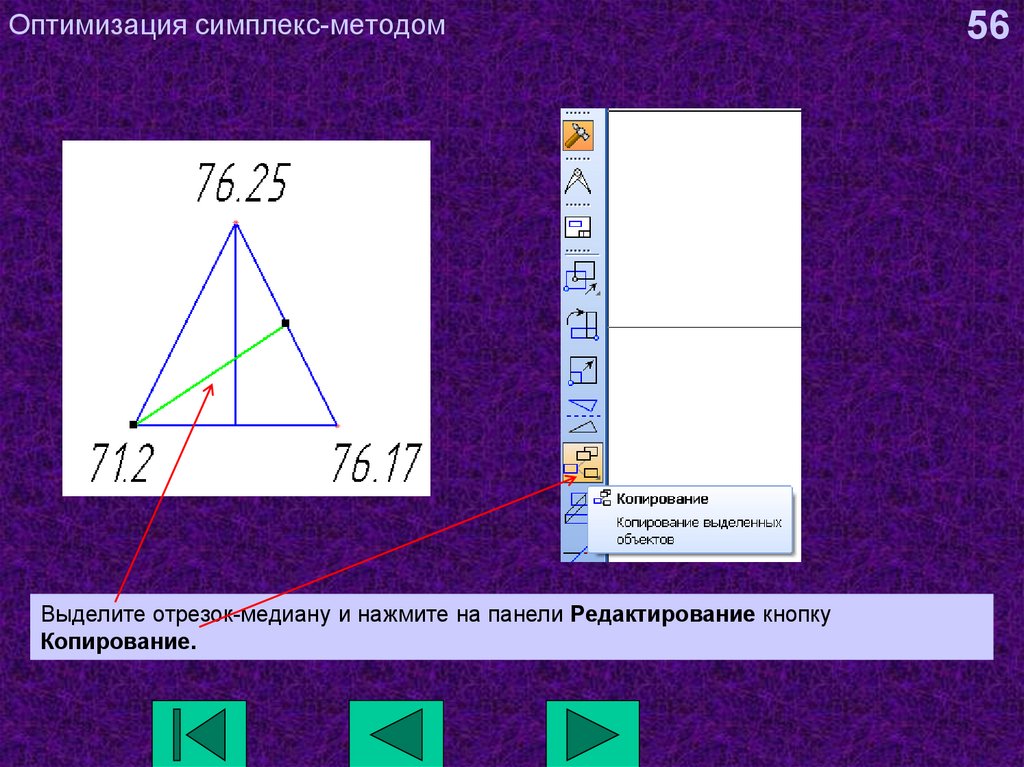
56. Оптимизация симплекс-методом

Выделите отрезок-медиану и нажмите на панели Редактирование кнопку
Копирование.
56

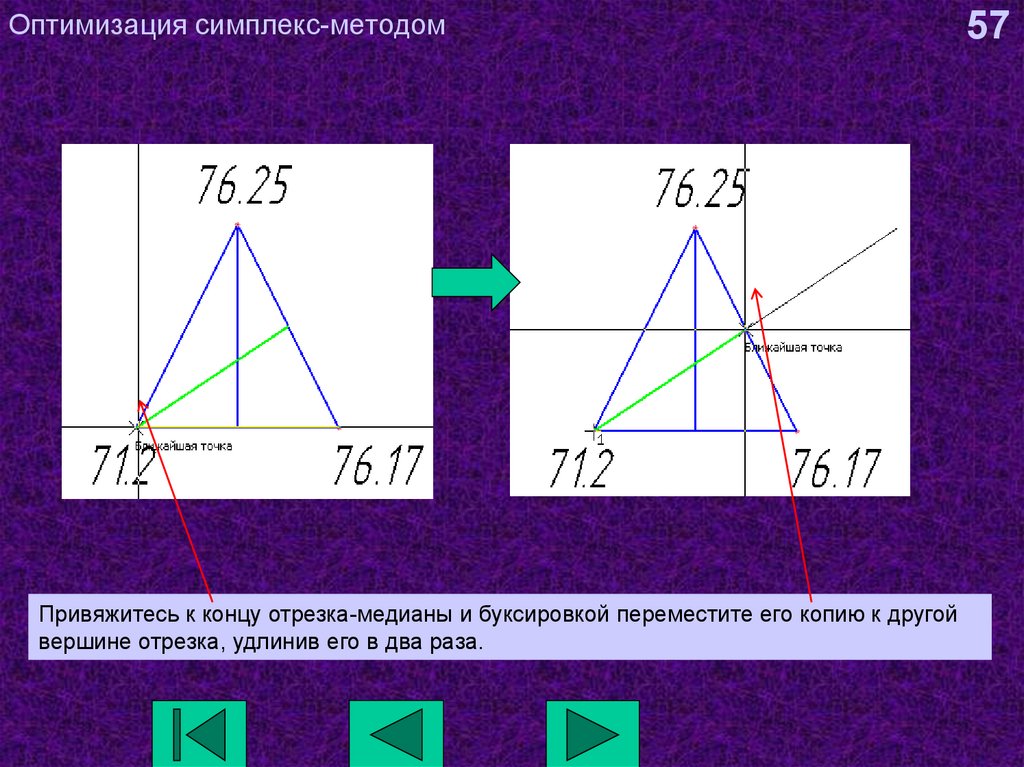
57. Оптимизация симплекс-методом

Привяжитесь к концу отрезка-медианы и буксировкой переместите его копию к другой
вершине отрезка, удлинив его в два раза.
57

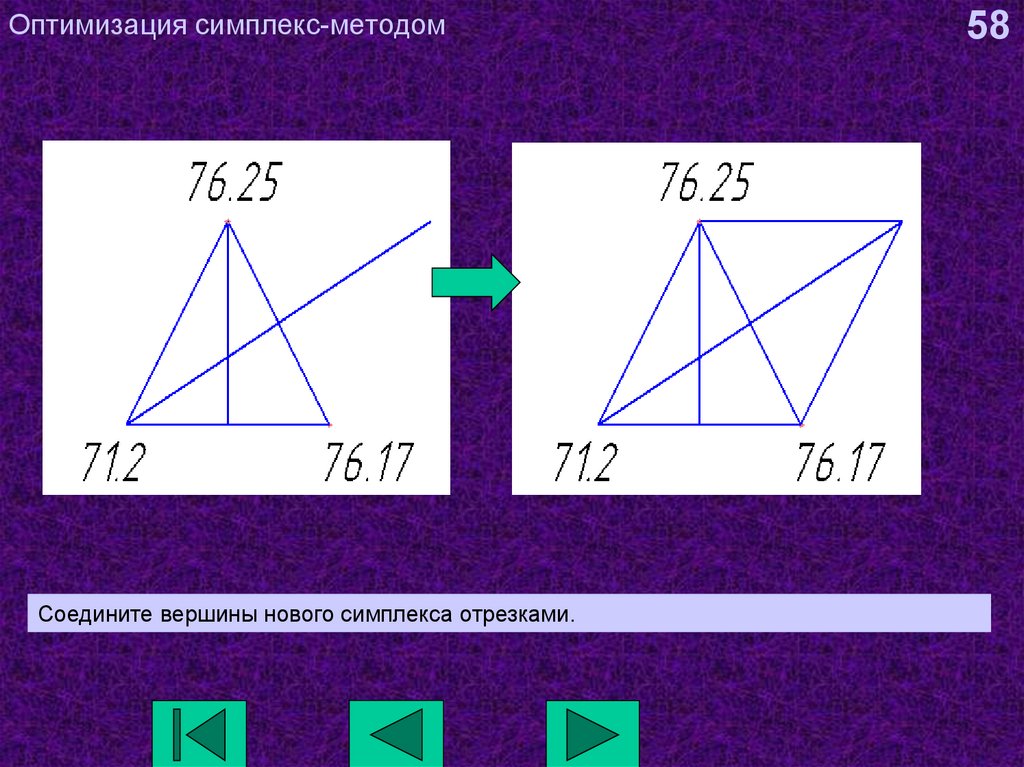
58. Оптимизация симплекс-методом

Соедините вершины нового симплекса отрезками.
58

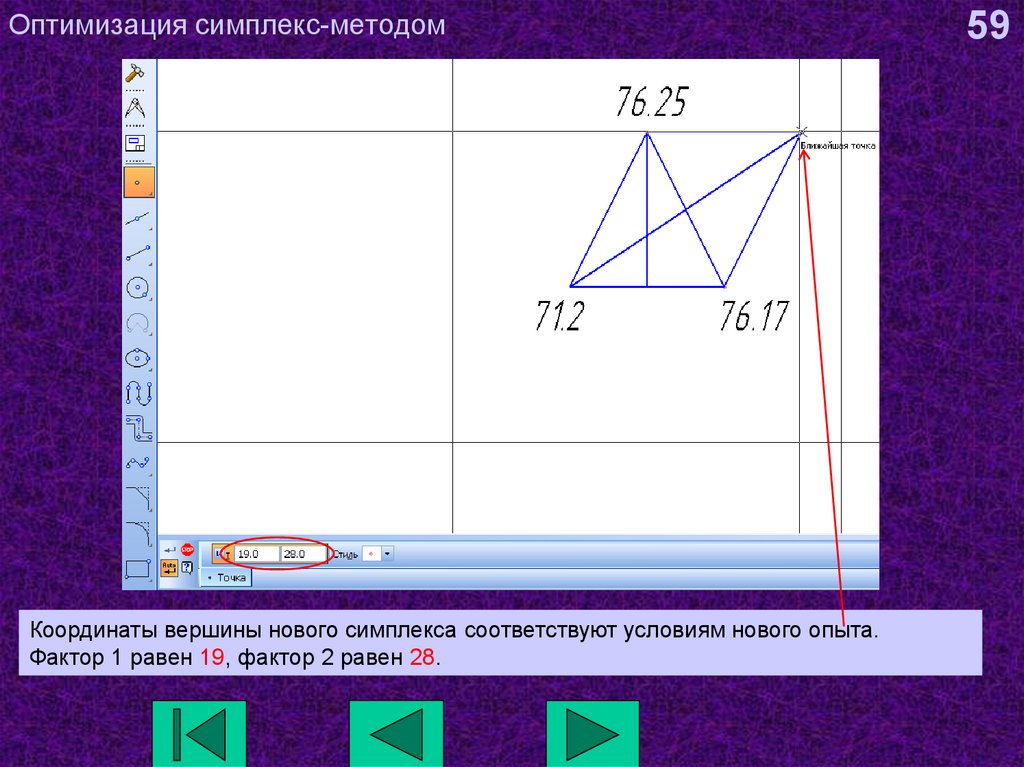
59. Оптимизация симплекс-методом

Координаты вершины нового симплекса соответствуют условиям нового опыта.
Фактор 1 равен 19, фактор 2 равен 28.
59

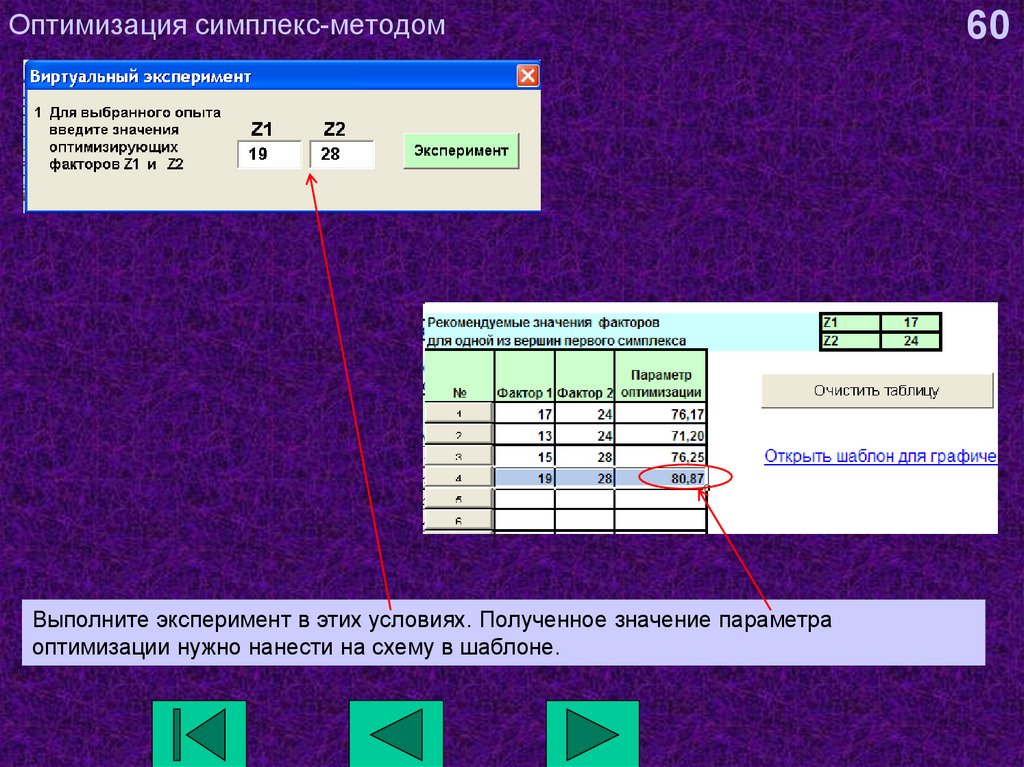
60. Оптимизация симплекс-методом

Выполните эксперимент в этих условиях. Полученное значение параметра
оптимизации нужно нанести на схему в шаблоне.
60

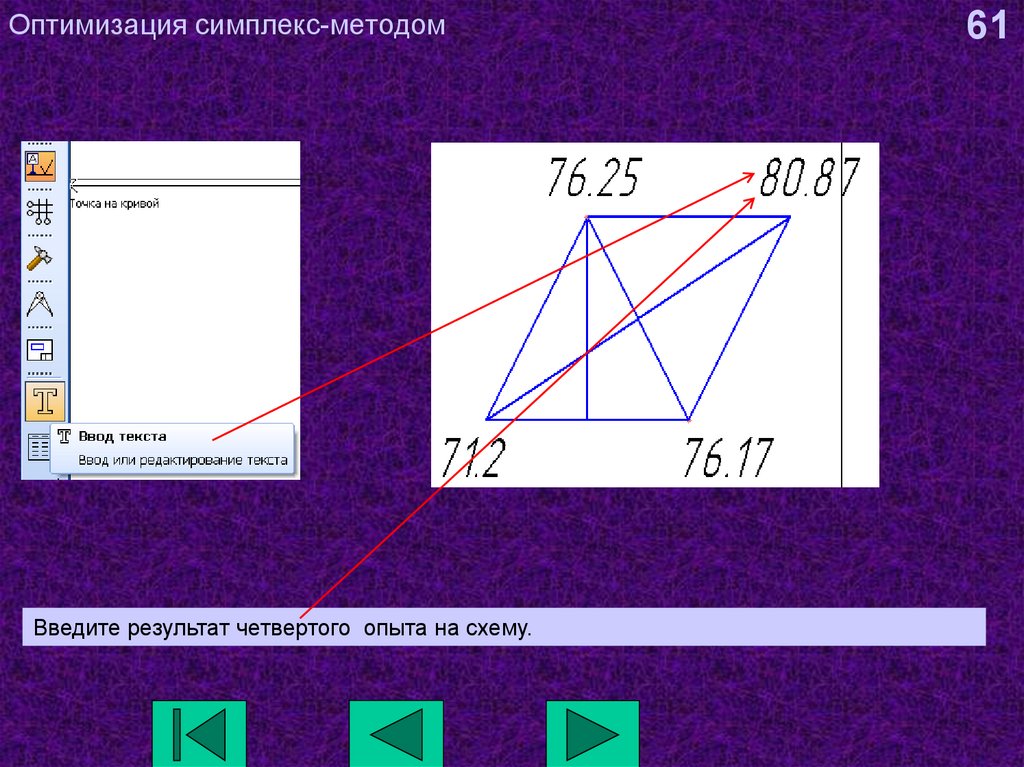
61. Оптимизация симплекс-методом

Введите результат четвертого опыта на схему.
61

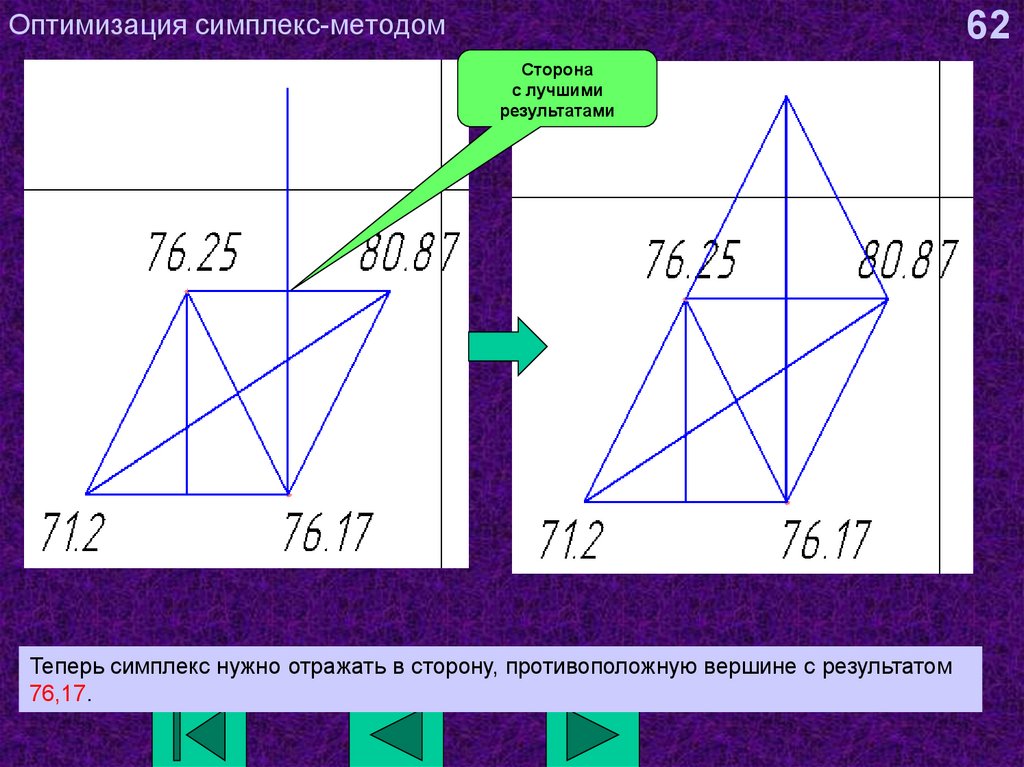
62. Оптимизация симплекс-методом

62
Сторона
с лучшими
результатами
Теперь симплекс нужно отражать в сторону, противоположную вершине с результатом
76,17.

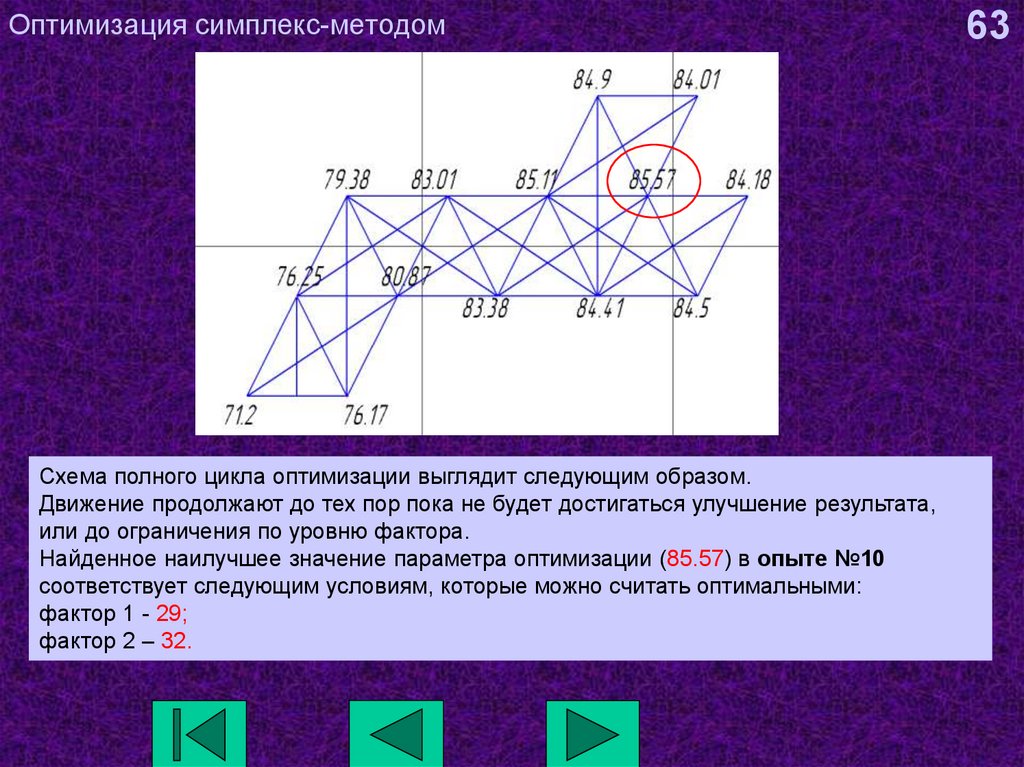
63. Оптимизация симплекс-методом

Схема полного цикла оптимизации выглядит следующим образом.
Движение продолжают до тех пор пока не будет достигаться улучшение результата,
или до ограничения по уровню фактора.
Найденное наилучшее значение параметра оптимизации (85.57) в опыте №10
соответствует следующим условиям, которые можно считать оптимальными:
фактор 1 - 29;
фактор 2 – 32.
63

64. Оптимизация симплекс-методом

Данное упражнение выполняется в среде Excel.
Откройте файл-шаблон упражнения с помощью приведенной ниже гиперссылки.
Ссылка для файла-шаблона данного упражнения
64

65.

Контрольные вопросы
1 В сущность метода оптимизации по Гауссу-Зайделю?
2 В чем достоинства метода Гаусса-Зайделя?
3 Какие недостатки метода Гаусса-Зайделя?
4 Что такое шаг при статистической оптимизации?
5 Какие критерии применяют при выборе шага?
6 В сущность симплекс-метода оптимизации?
7 В чем достоинства симплекс-метода?
8 Какие недостатки у симплекс-метода?
9 Как определяются условия проведения очередного опыта?
10 Когда заканчивают процесс оптимизации по симплекс-методу?

66.

Конец обучающего модуля