Синусоїдальний струм

1.

5 Синусоїдальний струм
Основні поняття
5.1 Змінний струм (напруга) і характеризують його величини
Змінним називається струм i(t) (напруга u(t)), періодично змінюється в
часі за довільним законом
i(t)=Im sin( t+ i ),
i u
Um
u(t)
Im
i (t)
i
u
T
Рисунок 5.1
u(t)=Umsin( t+ u)
u(t), i(t) або u, i миттєві значення функцій,
тобто їх значення в довільно обраний момент
t часу
Um, Im амплітудні (максимальні) значення
функцій
( t+ ) фаза, що визначається в момент
часу
u, i – початкові фази функцій, що визначають їх значення в момент t=0,
залежать від вибору початку відліку часу
= u i – кут зсуву фаз (різниця початкових фаз) між напругою і
струмом, не залежить від вибору початку відліку часу
1
Т – називається періодом
f
– частота.
2
2 f
T
T
с-1 або рад с – кутова частота

2.

5.2 Середнє і чинне значення змінного струму і напруги
Середнє значення Fср довільної функції часу f(t) за інтервал часу Т
визначається за формулою
T
1
Fcp f ( t ) dt
T 0
Для змінного синусоїдального струму (напруги) середнє значення
визначають за половину періоду (Т/2) між двома нульовими значеннями
1
I ср
Т
2
Т
2
2Im
I
sin
t
dt
m
0
T
2Im
cos
t
0
0 sin t d ( t ) 2 Т
T
Діючі значення змінного струму (напруги)
середньоквадратичне значення функції за період
2 Im
0 ,637 I m
визначається
як
T
T
T
Im
I 2m 1
1
1 2 2
I 2m 1 1
2
0 ,707 I m
T
I
i
(
t
)
dt
I
sin
t
dt
cos
2
t
dt
m
T 2
T0
T0
T 0 2 2
2
В електроенергетиці прийнято всі теоретичні розрахунки та
експериментальні вимірювання виконувати для діючих значень струмів і
напруг.
коефіцієнт амплітуди K a
коефіцієнт форми
KФ
Im Um
2 1 ,41
I
U
I
U
0 ,707
1 ,11
I ср U ср 0 ,637

3.

5.3 Векторні діаграми змінних струмів і напруг
З курсу математики відомо, що будь-яку синусоїдальну функцію часу,
наприклад i(t)=Imsin( t+Ψ), можна зобразити обертовим вектором при
дотриманні наступних умов
а) довжина вектора в масштабі дорівнює амплітуді функції Im;
б) початкове положення вектора при t = 0 визначається початковою фазою Ψ
в) вектор рівномірно обертається з кутовою швидкістю , рівний кутовий
частоті функції
y
A2
ω
a
Am sin(ωt+ψ)
A1
Am
ωt
x
ψ
ωt+ψ
I
Рисунок 5.2
I1
I2
1 2
Рисунок 5.3
Нехай задані два струми, записані у вигляді
синусоїдальних функцій
i1 I 1m sin( t 1 ) i2 I 2 m sin( t 2 )
Знайдемо їх суму у вигляді векторної діаграми (рис. 5.3)

4.

5.4 Теоретичні основи комплексного методу розрахунку кіл змінного струму
Зобразимо вектор струму на комплексній площині
+j
I
Ip
Ia
Комплексне число може бути представлено у наступних
трьох формах
I I a jI p
1) алгебраїчній
I a I cos
+1 Ia – дійсна частина комплексного числа
Ip – уявна частина комплексного числа I p I sin
j – уявне одиничне число
2) тригонометричній
3) показниковій
I I cos jI sin
I Ie j
I I a2 I p2
Ip
Ψ аргумент комплексного числа arctg
Ia
I – модуль комплексного числа
Наведемо чисельні співвідношення, які найбільш часто зустрічаються
e
j0
1 e
j 180
1 e
j 90
j e
j 90
j
j 1
2
1
j
j
4

5.

5.4 Теоретичні основи комплексного методу розрахунку кіл змінного струму
Розглянемо основні математичні операції з комплексними числами.
Припустимо, що задані два числа, які записані в алгебраїчній і показниковій формах.
A a1 ja 2 Ae
j
B b1 jb2 Be j
Додавання (віднімання) комплексних чисел проводиться в алгебраїчній формі
A B ( a1 ja 2 ) ( b1 jb2 ) ( a1 b1 ) j( a 2 b2 )
Множення (ділення) комплексних чисел може виконуватися
в алгебраїчній формі
B
A B Ae j Be j A Be j ( )
в показниковій формі
A
A B ( a1 ja 2 ) ( b1 jb2 ) ( a1b1 a2 b2 ) j( a1b2 a2 b1 )
( a1 ja 2 ) ( a1 ja 2 ) ( b1 jb2 ) a1b1 a2 b2 j( a2 b1 a1b2 )
( b1 jb2 ) ( b1 jb2 ) ( b1 jb2 )
b12 b22
a1b1 a2 b2
a2 b1 a1b2
j
.
b12 b22
b12 b22
Ae j A j ( )
e
.
j
Be
B
B
A
Піднесення до степеня (добування кореня) комплексного числа виконується тільки в
показниковій формі
j
A ( A e ) A e
n
n
jn
A
A e
j
A e
j2

6.

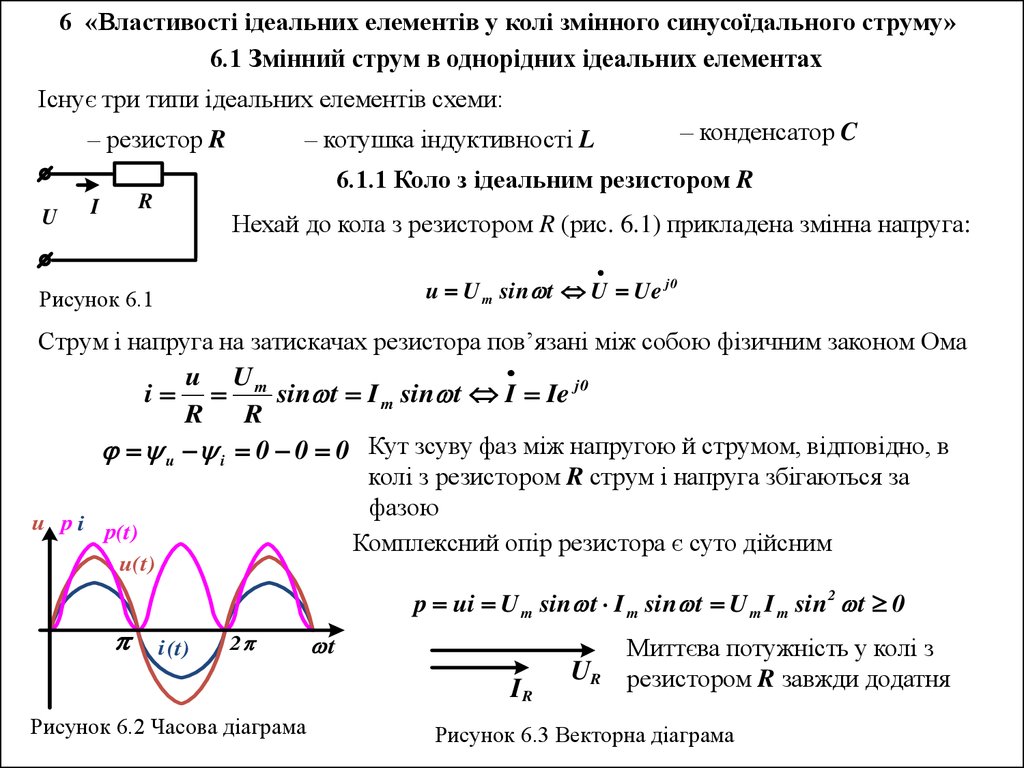
6 «Властивості ідеальних елементів у колі змінного синусоїдального струму»
6.1 Змінний струм в однорідних ідеальних елементах
Існує три типи ідеальних елементів схеми:
– резистор R
U
6.1.1 Коло з ідеальним резистором R
R
I
– конденсатор C
– котушка індуктивності L
Нехай до кола з резистором R (рис. 6.1) прикладена змінна напруга:
u U m sin t U Ue j 0
Рисунок 6.1
Струм і напруга на затискачах резистора пов’язані між собою фізичним законом Ома
u Um
i
sin t I m sin t I Ie j 0
R
R
u i 0 0 0 Кут зсуву фаз між напругою й струмом, відповідно, в
колі з резистором R струм і напруга збігаються за
фазою
u p i p(t)
Комплексний опір резистора є суто дійсним
u(t)
p ui U m sin t I m sin t U m I m sin 2 t 0
i (t)
2
t
IR
Рисунок 6.2 Часова діаграма
UR
Миттєва потужність у колі з
резистором R завжди додатня
Рисунок 6.3 Векторна діаграма

7.

U
I
6.1.2 Коло з ідеальною котушкою L
Нехай до кола з ідеальною котушкою L (рис. 6.4) прикладена змінна
напруга
u U m sin t U Ue j 0
L
Рисунок 6.4
Струм та напруга на затискачах котушки пов’язані між собою
законом електромагнітної індукції
U
1
i uL dt m
L
L
uL e L
di
dt
Um
o
j 90o
sin
t
dt
(
cos
t
)
I
sin(
t
90
)
I
Ie
m
L
Рівняння закону Ома для амплітудних та дійсних значень функцій
X L L індуктивний реактивний опір котушки
Im
u i 0 ( 90 0 ) 90 0 кут зсуву фаз 900 .
Um
U
,I
XL
XL
У колі з котушкою L струм відстає від напруги (напруга випереджає струм)
Комплексний опір котушки є суто уявним і додатнім
U
Um Im
U I
U I
cos 90 o m m cos( 2 t 90 o ) m m sin 2 t
2
2
2
ui p
p(t)
i (t)
u (t)
2
Рисунок 6.5
Ie j 90
0
U j 90 0
e
j L jX L
I
Миттєва потужність кола змінюється
за синусоїдальним законом з
частотою 2 :
90 0
Це означає, що в колі з котушкою L
IL
відбувається лише періодичний
Рисунок 6.6 процес обміну енергією .
UL
t
I
Ue j 0

8.

U
C
I
Рисунок 6.7
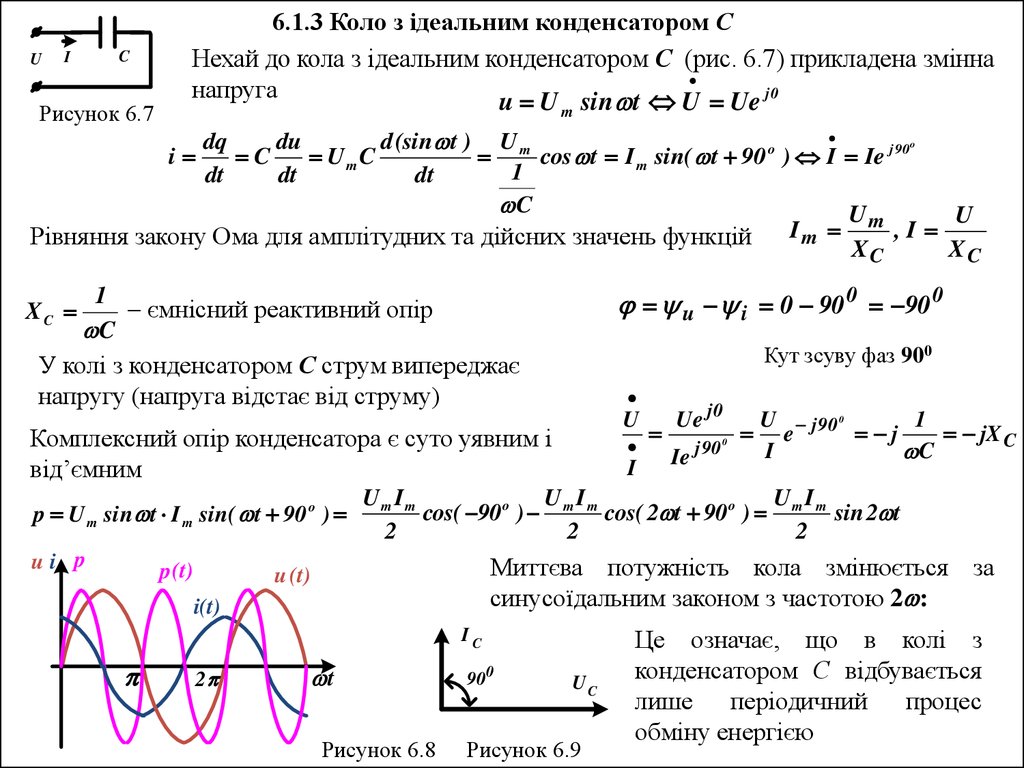
6.1.3 Коло з ідеальним конденсатором С
Нехай до кола з ідеальним конденсатором С (рис. 6.7) прикладена змінна
напруга
u U sin t U Ue j 0
m
o
dq
du
d (sin t ) U m
C
U mC
cos t I m sin( t 90 o ) I Ie j 90
1
dt
dt
dt
C
Um
U
I
,I
m
Рівняння закону Ома для амплітудних та дійсних значень функцій
XC
XC
i
XC
u i 0 90 0 90 0
1
ємнісний реактивний опір
C
Кут зсуву фаз 900
У колі з конденсатором С струм випереджає
напругу (напруга відстає від струму)
U
Комплексний опір конденсатора є суто уявним і
від’ємним
p U m sin t I m sin( t 90 o )
ui p
p (t)
I
0
U j 90 0
1
e
j
jX C
I
C
Миттєва потужність кола змінюється за
синусоїдальним законом з частотою 2 :
u (t)
IC
2
Ie j 90
Um Im
U I
U I
cos( 90 o ) m m cos( 2 t 90 o ) m m sin 2 t
2
2
2
i(t)
Ue j 0
t
Рисунок 6.8
90 0
UC
Рисунок 6.9
Це означає, що в колі з
конденсатором С відбувається
лише періодичний процес
обміну енергією

9.

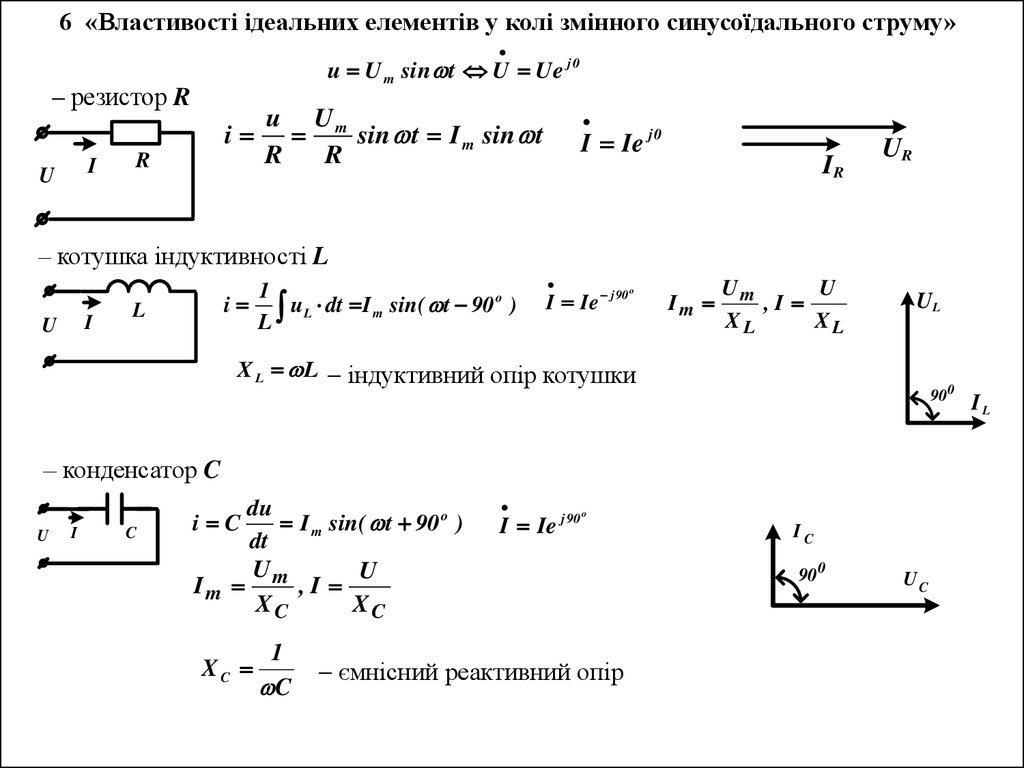
6 «Властивості ідеальних елементів у колі змінного синусоїдального струму»
u U m sin t U Ue j 0
– резистор R
i
I
U
R
u Um
sin t I m sin t
R
R
I Ie j 0
IR
UR
– котушка індуктивності L
I
U
1
i uL dt I m sin( t 90 o )
L
L
I Ie j 90
o
Im
Um
U
,I
XL
XL
UL
X L L індуктивний опір котушки
90 0
– конденсатор C
U
I
C
du
i C
I m sin( t 90 o )
dt
U
U
Im m , I
XC
XC
XC
1
C
I Ie j 90
o
ємнісний реактивний опір
IC
90 0
UC
IL

10.

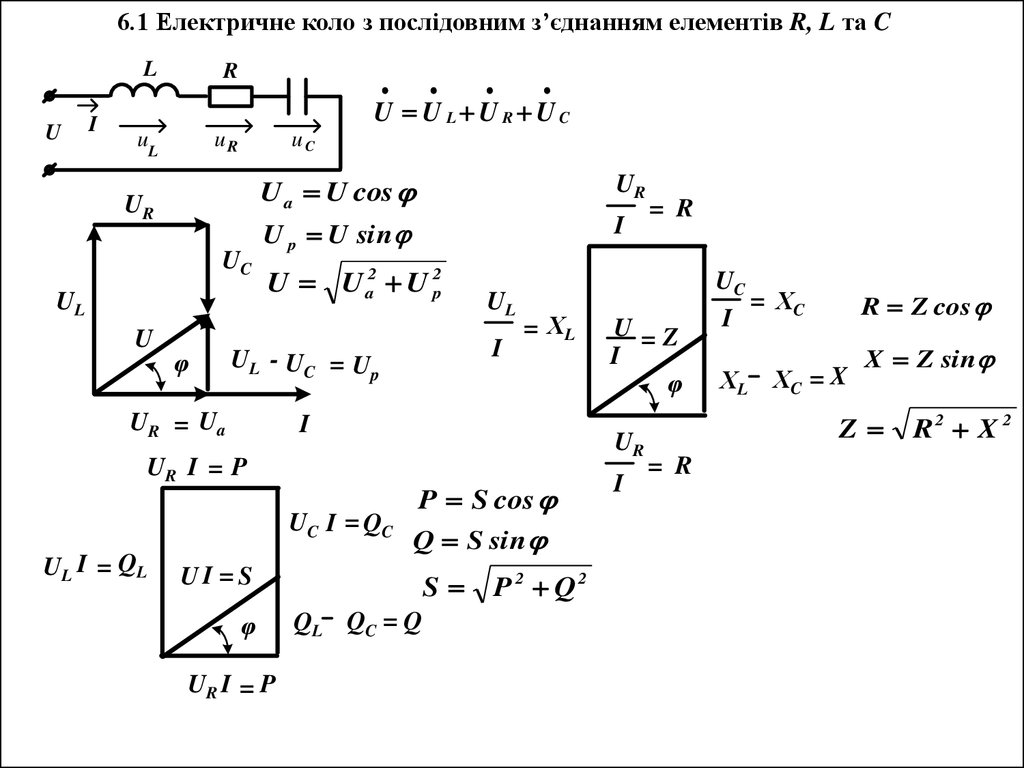
6.1 Електричне коло з послідовним з’єднанням елементів R, L та C
L
U
I
R
U U L U R UC
uL
uR
uC
UR
UC
UL
U
U a U cos
UR
U p U sin
I
U U a2 U p2
φ
UL - UC = Up
UR = Ua
I
UR I = P
UC I = QC
UL I = QL
I
UR I = P
= ХL
U =Z
I
φ
UR
P S cos
Q S sin
UI =S
φ
UL
S
QL QC = Q
P 2 Q2
= R
I
UC
= ХC
I
ХL
R Z cos
ХC = X
X Z sin
Z
= R
R2 X 2

11.

6.1 Електричне коло з послідовним з’єднанням елементів R, L та C
L
R
Нехай у заданій схемі з послідовним з’єднанням елементів
R, L та C (рис. 6.10) протікає змінний струм
I
U
uL
uR
uC
i I m sin t I Ie j 0
рівняння в комплексній формі
Рисунок 6.10
U U L U R U C I R I jX L I jX C I ( R jX L jX C ) I Z
где Z ( R jX L jX C ) комплексний опір,
X X L X C реактивний опір
Z
R 2 ( X L X C )2
модуль комплексного опору або повний опір
X L XC
R
аргумент комплексного опору або кут зсуву фаз між напругою
та струмом на вході схеми
При φ>0, при цьому коло має активно-індуктивний характер
arctg
при φ<0 – коло має активно-ємнісний характер.
Рівняння закону Ома для послідовної схеми матиме вигляд
I
U
U
Z R j( X L X C )
I
U
Z
в комплексній формі,
U
2
R ( X L XC )
2
в звичайній формі для модулів

12.

6.2 Електричне коло з паралельним з’єднанням елементів R, L та С
Векторна діаграма струмів і напруги при φ>0 показана
на рисунку 6.2.
I
L
U
IL
R
IR
C
IR
IC
U
Рисунок 6.1
IR = Ia
φ
IL
I
IR
Рисунок 6.2
U
IL
IL
IC = Ip
U
I a I cos
I p I sin
IC
I
I a2 I p2
= BL
= G
I =Y
U
φ
IR
U
IC
= BC
U
BL
G Y cos
BC = B
B Y sin
Y G 2 B2
= G
Рисунок 6.3

13.

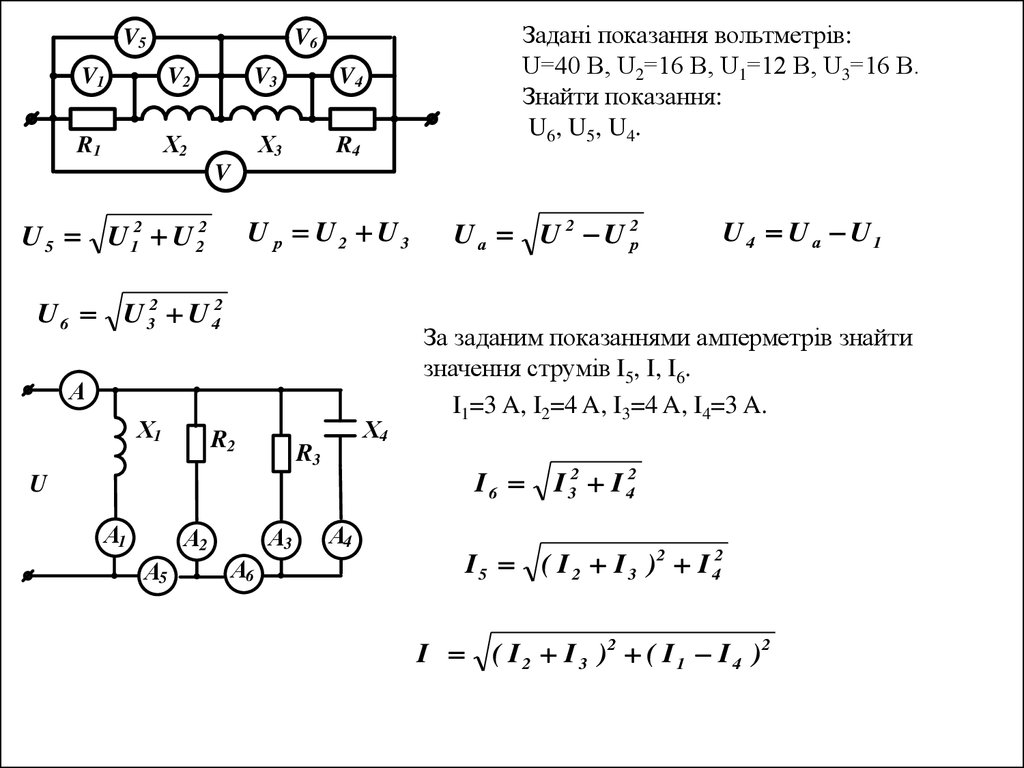
Задані показання вольтметрів:
U=40 В, U2=16 В, U1=12 В, U3=16 В.
Знайти показання:
U6, U5, U4.
V6
V5
V1
V2
V3
V4
R1
Х2
Х3
R4
V
U р U2 U3
U 5 U 12 U 22
U 6 U 32 U 42
А
Х1
R2
Х4
R3
А3
А2
А5
А6
А4
U4 Uа U1
За заданим показаннями амперметрів знайти
значення струмів I5, I, I6.
I1=3 A, I2=4 A, I3=4 A, I4=3 A.
I6
U
А1
U а U 2 U р2
I 32 I 42
I 5 ( I 2 I 3 )2 I 42
I ( I 2 I 3 )2 ( I 1 I 4 )2

14.

6.2 Електричне коло з паралельним з’єднанням елементів R, L та С
Нехай на вході схеми діє змінна напруга:
I
L
U
IL
R
IR
u U m sin t U Ue j 0
C
IC
рівняння в комплексній формі
U
U
U
I I L I R I C R jX jX U ( G jB L jBC ) U Y
L
C
Y комплексна провідність
G
1
R
BL
Y G jBL jBC G jB
активна провідність
1
індуктивна провідність
XL
BC
1
XC
ємнісна провідність
B BL BC реактивна (еквівалентна) провідність
Y G 2 B 2 модуль комплексної провідності або повна провідність
BL BC
arctg
G
аргумент комплексної провідності або кут зсуву фаз
між напругою та струмом на вході схеми
При (ВL–BC) >0 и φ>0 – коло в цілому має активно-індуктивний характер
при (ВL–BC) <0 и φ<0 – коло в цілому має активно-ємнісний характер

15.

7 «Еквівалентні перетворення електричних кіл змінного струму»
7.1 Еквівалентні перетворення опорів та провідностей
XL
R
I
I
U
Ua
U
Up
BL
Ip
Рисунок 7.1
Ia
Обидві схеми будуть еквівалентні
один до одного за умови рівності
G
параметрів режиму на вході, тобто
напруги й струму
Рисунок 7.2
Для послідовної схеми (рис. 7.1) справедливі співвідношення
U
U ( R jX L )
U ( R jX L )
R
XL
I
U
j
U Y
2
2
R2 X 2
R jX L ( R jX L ) ( R jX L )
R2 X L
R 2 X L
L
Для паралельної схеми (рис. 7.2) справедливі співвідношення
G
BL
I
I ( G jB L ) I
I ( G jB L )
j
U
I
Z
2
2
G2 B 2
G
B
G jB L ( G jB L ) ( G jB L ) G 2 BL 2
L
L
Порівнюючи праві частини рівнянь отримаємо співвідношення між параметрами
еквівалентних схем
G
R
R
R
2
R2 X L
Z2
1
G
X
1
B
B
X
X
2
Z2
R2 X L
R
G
G
2
G 2 BL
Y2
X
BL
2
G BL
2
BL
Y2

16.

7.1 Еквівалентні перетворення опорів та провідностей
U
Up
Ua
I
U a U cos , U p U sin ,
Рисунок 7.3
R
Рисунок 7.4
X Z sin
R Z cos
Ip
U
Ia
Рисунок 7.5
I a I cos
G
Рисунок 7.6
B
Z
R2 X 2
arctg
X
.
R
Паралельній схемі заміщення (рис. 7.2) відповідає представлення вектора
струму у вигляді суми двох складових:
активної складової Iа, яка збігається з вектором напруги U,
й реактивної складової Iр, перпендикулярної до вектора U (рис. 7.5).
З отриманого трикутника струмів (рис. 7.5) слідують співвідношення:
I p I sin
Y
U U a2 U p2 .
Якщо сторони трикутника напруг поділити на струм I, то отримаємо новий
трикутник опорів, подібний вихідному, гіпотенузою
X якого є повний опір, катетами – активний опір R
і реактивний опір X.
З трикутника опорів (рис. 7.4) слідують співвідношення:
Z
I
Послідовній схемі заміщення (рис. 7.1) відповідає представлення вектора
напруги у вигляді суми двох складових:
активної складової Uа, яка збігається з вектором струму I,
й реактивної складової Uр, перпендикулярної до вектора струму (рис. 7.3).
I
I a2 I p2 .
Якщо сторони трикутника струмів (рис 7.5) поділити на напругу U, то
отримаємо новий трикутник провідностей (рис. 7.6), подібний вихідному.
Y – повна провідність
B - реактивна провідність
G – активна провідність

17.

8 «Застосування законів Кірхгофа»
8.1 Основи комплексного обчислення кіл синусоїдального струму
Символічний метод обчислення кіл синусоїдального струму заснований на законах Кірхгофа та
законі Ома в комплексній формі
Рівняння, що виражають закони Кірхгофа в комплексній формі, мають цілком такий же вигляд,
як і відповідні рівняння для кіл постійного струму.
Тільки струми, ЕРС, напруги й опори входять в рівняння у вигляді комплексних величин.
I 0
Перший закон Кірхгофа в комплексній формі:
Другий закон Кірхгофа в комплексній формі:
U E
Розглянемо застосування законів Кірхгофа для розгалуженого електричного кола (рис. 8.1),
параметри: U=120 B X1=100 Oм R1= 25 Oм X2=50 Oм R2= 20 Oм
I1
a
X3=50 Oм. Визначити струми у гілках електричного кола.
R1
X1
Скласти рівняння балансу потужності
X3
X2
Розв’язання
U
I2
1 Запишемо вираз для визначення еквівалентного опору кола:
I3
R
2
b
Z ЭКВ R1 jX 1
Z ЭКВ 25 j 100
( R2 jX 2 )( jX 3 )
.
R2 jX 2 jX 3
( 20 j 50 )( j 50 )
150 j 150 Ом.
20 j 50 j 50
2 Приймемо початкову фазу джерела за нуль, запишемо:
3 Визначимо перший струм за законом Ома:
U
I1
Z ЭКВ
U Ue j 0 120 B .
120
0 ,4 j 0 ,4 A.
150 j150

18.

8 «Застосування законів Кірхгофа»
8.1 Основи комплексного обчислення кіл синусоїдального струму
Символічний метод обчислення кіл синусоїдального струму заснований на законах Кірхгофа та
законі Ома в комплексній формі
Рівняння, що виражають закони Кірхгофа в комплексній формі, мають цілком такий же вигляд,
як і відповідні рівняння для кіл постійного струму.
Тільки струми, ЕРС, напруги й опори входять в рівняння у вигляді комплексних величин.
Перший закон Кірхгофа в комплексній формі:
Другий закон Кірхгофа в комплексній формі:
I 0
U E
Розглянемо застосування законів Кірхгофа для розгалуженого електричного кола (рис. 8.1),
параметри: U=120 B X1=100 Oм R1= 25 Oм X2=50 Oм R2= 20 Oм
I1
a
X3=50 Oм. Визначити струми у гілках електричного кола.
R1
X1
Скласти рівняння балансу потужності
X3
X2
Розв’язання
U
I2
1 Запишемо вираз для визначення еквівалентного опору кола:
I3
R
2
Z ЭКВ R1 jX 1
( R2 jX 2 )( jX 3 )
R2 jX 3 X 2 X 3
R1 jX 1
R2 jX 2 jX 3
R2 jX 2 jX 3
b
X X jR2 X 3 R2 j ( X 2 X 3 )
X X R R2 jR2 X 3 X 2 X 3 j ( X 2 X 3 ) R2 X 3 ( X 2 X 3 )
R1 jX 1 2 3
R1 jX 1 2 3 2
R2 j ( X 2 X 3 ) R2 j ( X 2 X 3 )
R22 ( X 2 X 3 ) 2
R11
X 2 X 3 R2 R2 X 3 ( X 2 X 3 )
R2 R2 X 3 X 2 X 3 ( X 2 X 3 )
j ( X 1
)
2
2
R2 ( X 2 X 3 )
R22 ( X 2 X 3 ) 2

19.

Z ЭКВ 25 j 100
( 20 j 50 )( j 50 )
150 j 150 Ом.
20 j 50 j 50
2 Приймемо початкову фазу джерела за нуль, запишемо:
3 Визначимо перший струм за законом Ома: I 1 U
Z ЭКВ
U Ue j 0 120 B .
120
0 ,4 j 0 ,4 A.
150 j150
4 Знаходимо напругу між вузлами “а” та “b” Uab:
U ab U I 1 ( R1 jX 1 ) 120 ( 0 ,4 j 0 ,4 )( 25 j 100 ) 70 j 30
5 Тоді струми в другій та третій гілках знайдемо за законом Ома:
U ab
70 j 30
I2
1 j1 A,
20 j 50
R2 jX 2
I3
U ab
70 j 30
jX 3
j 50
0 ,6 j 1,4 A
6 Складаємо рівняння балансу потужності
S ИСТ S НАГР
S
ИСТ
P
НАГР
Q
НАГР
U I 1 120( 0 ,4 j 0 ,4 ) 48 j 48 Р ИСТ jQИСТ
I 12 R1 I 22 R2 ( 0 ,4 2 0 ,4 2 )25 ( 12 12 )20 8 40 48 Вт
I 12 ( X 1 ) I 22 X 2 I 32 ( X 3 ) ( 0 ,4 2 0 ,4 2 )( 100 ) ( 12 12 )50 ( 0 ,6 2 1,4 2 )( 50 )
32 100 116 48 ВАр

20.

Z ЭКВ 25 j 100
( 20 j 50 )( j 50 )
150 j 150 Ом.
20 j 50 j 50
2 Приймемо початкову фазу джерела за нуль, запишемо:
3 Визначимо перший струм за законом Ома: I 1 U
Z ЭКВ
U Ue j 0 120 B .
120
0 ,4 j 0 ,4 A.
150 j150
4 Знаходимо напругу між вузлами “а” та “b” Uab:
U ab U I 1 ( R1 jX 1 ) 120 ( 0 ,4 j 0 ,4 )( 25 j 100 ) 70 j 30
5 Тоді струми в другій та третій гілках знайдемо за законом Ома:
I2
U ab
70 j 30
1 j1 A,
R2 jX 2
20 j 50
I3
U ab
70 j 30
jX 3
j 50
0 ,6 j 1,4 A
6 Складаємо рівняння балансу потужності
S ИСТ S НАГР
S
ИСТ
P
НАГР
Q
НАГР
U I 1 120( 0 ,4 j 0 ,4 ) 48 j 48 Р ИСТ jQИСТ
I 12 R1 I 22 R2 ( 0 ,4 2 0 ,4 2 )25 ( 12 12 )20 8 40 48 Вт
I 12 ( X 1 ) I 22 X 2 I 32 ( X 3 ) ( 0 ,4 2 0 ,4 2 )( 100 ) ( 12 12 )50 ( 0 ,6 2 1,4 2 )( 50 )
32 100 116 48 ВАр

21.

Резонанс в електричних колах
Визначення резонансу
В електричному колі, яке містить котушки індуктивністю L й конденсатори C, можливі вільні
гармонічні коливання енергії між магнітним полем котушки
Li 2
WM
Cu2
2
та електричним полем конденсатора WЭ
2
В резонансному режимі коливання енергії між магнітними й електричними полями
замикаються всередині кола
Обмін енергією між джерелом та колом відсутній
Електричне коло по відношенню до джерела енергії веде себе як суто активний опір R
(активна провідність G).
Умова для резонансного режиму через параметри елементів схеми:
- вхідний опір Zвх=Rвх
- вхідна провідність Yвх=Gвх
схеми з боку виводів джерела енергії повинні мати чисто активний характер

22.

Резонанс напруг
Резонанс в колі з послідовним з’єднанням джерела енергії й реактивними елементами L та C
отримав назву резонансу напруг.
L
R
Xэ= XL XC =0
Умова резонансу напруг:
або
U
I
uL
uR
0 L
uC
1
0 0
0 C
1
резонансна або власна частота.
LC
З отриманої рівності слідує, що резонансного режиму в колі можна досягти зміною параметрів
елементів L та C або частоти джерела .
В резонансному режимі повний опір схеми має мінімальне значення й рівне активному опору:
Z
R 2 X L X C R,
2
Струм максимальний і збігається за фазою з напругою джерела: I=U/R; = 0.
UL
UR
Напруга на резисторі рівна напрузі джерела: UR=IR=U.
UC
Напруга на реактивних елементах рівні за модулем, протилежні за
фазою й взаємно компенсують один одного:
U L IX L
UR =U
I
U
XL
R
U C IX C
U
XC .
R
Напруги на реактивних елементах
U L UC U
можуть значно перевищувати напругу джерела U за умови, що XL=XC>>R.
X
XL
U C
R
R

23.

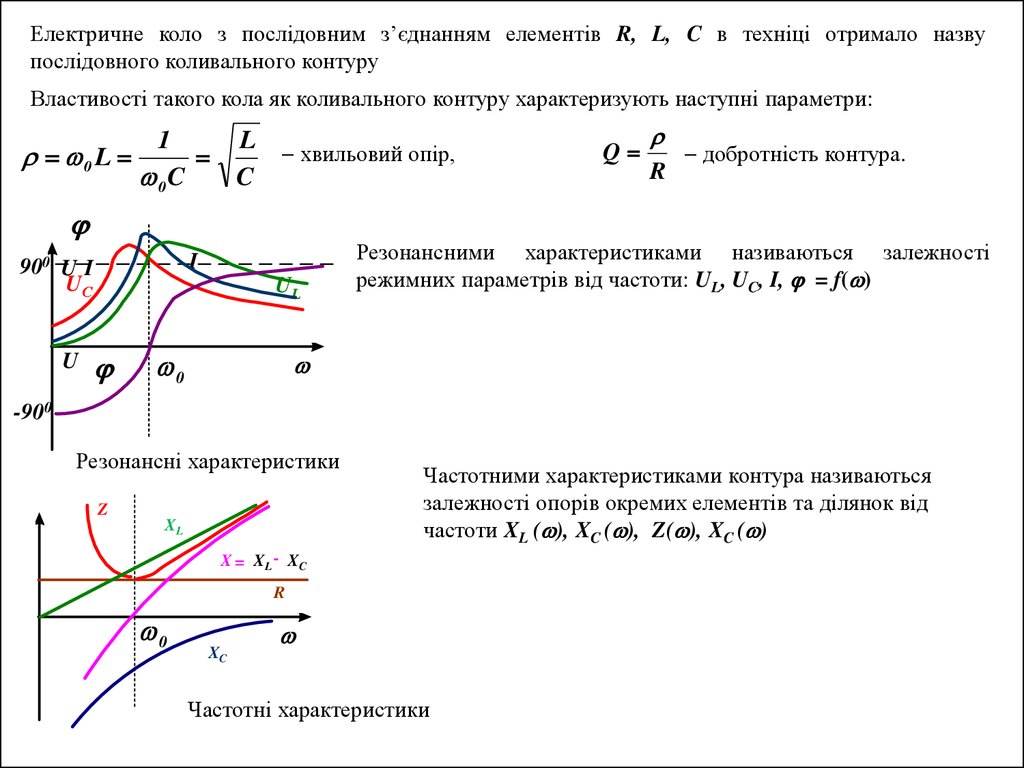
Електричне коло з послідовним з’єднанням елементів R, L, C в техніці отримало назву
послідовного коливального контуру
Властивості такого кола як коливального контуру характеризують наступні параметри:
1
0 L
0 C
L
C
хвильовий опір,
I
900 U I
UС
U
UL
0
Q
R
добротність контура.
Резонансними характеристиками називаються залежності
режимних параметрів від частоти: UL, UC, I, = f( )
-900
Резонансні характеристики
Z
XL
Частотними характеристиками контура називаються
залежності опорів окремих елементів та ділянок від
частоти XL ( ), XC ( ), Z( ), XC ( )
X = X L - XC
R
0
XC
Частотні характеристики

24.

Резонанс струмів
Резонанс в колі з паралельним з’єднанням джерела енергії й реактивних елементів L та C
отримав назву резонансу струмів.
Умова резонансу струмів: b bL bC 0
I
L
U
IR
IL
g
R
1
,
R
IC
bL
1
,
L
C
1
0 C 0 0
0 L
bL bC
1
резонансна (власна) частота.
LC
В резонансному режимі повна провідність схеми рівна активній
провідності й має мінімальне значення:
Y
g 2 bL bC g
2
bC C
Струм джерела також мінімальний й збігається за фазою з напругою джерела ( = 0):
I =UY = Ug.
Струми в гілках з реактивними елементами
IL= UbL, IC =UbC рівні за модулем,
протилежні за фазою й компенсують один одного
Струм в резисторі R рівний струму джерела (I=IR=Ug).
IR
IC
I R= I
За умови, що bL=bC>>g струми в реактивних елементах IL = IC
можуть значно перевищувати струм джерела I
IL Електричне коло з паралельним з’єднанням елементів R, L та C в техніці
U отримало назву паралельного коливального кола.

25.

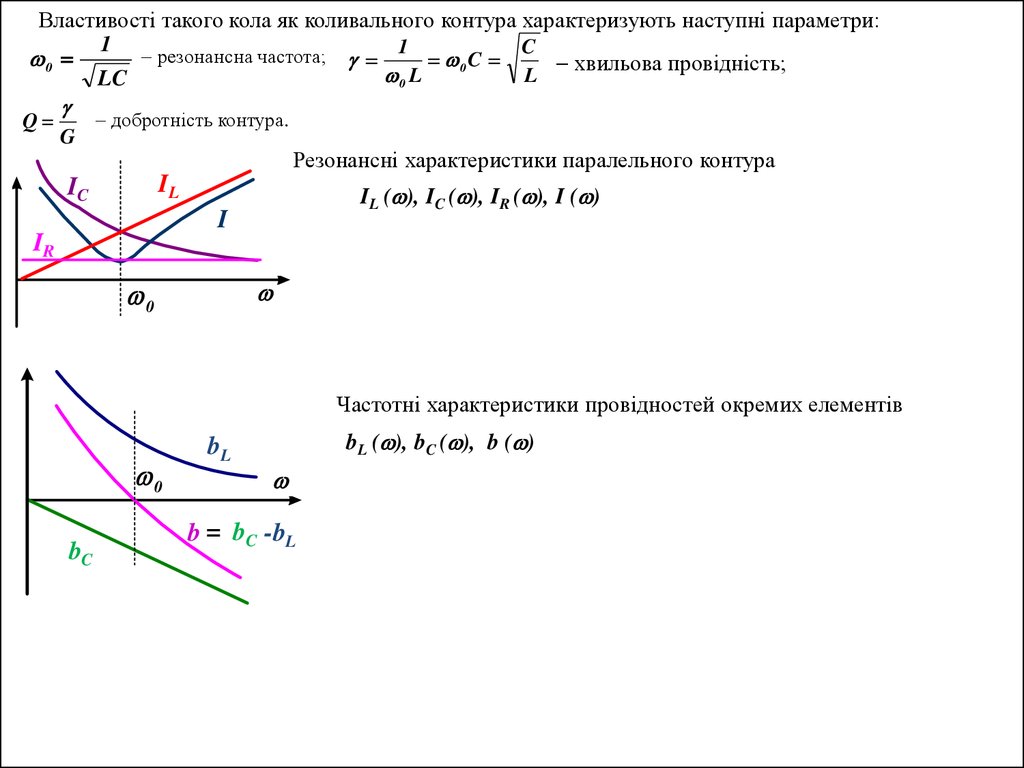
Властивості такого кола як коливального контура характеризують наступні параметри:
1
резонансна частота; 1 0 C C хвильова провідність;
0
0 L
L
LC
Q
G
добротність контура.
Резонансні характеристики паралельного контура
IL
IC
IL ( ), IC ( ), IR ( ), I ( )
I
IR
0
Частотні характеристики провідностей окремих елементів
0
bC
bL
bL ( ), bC ( ), b ( )
b = bC -bL

26.

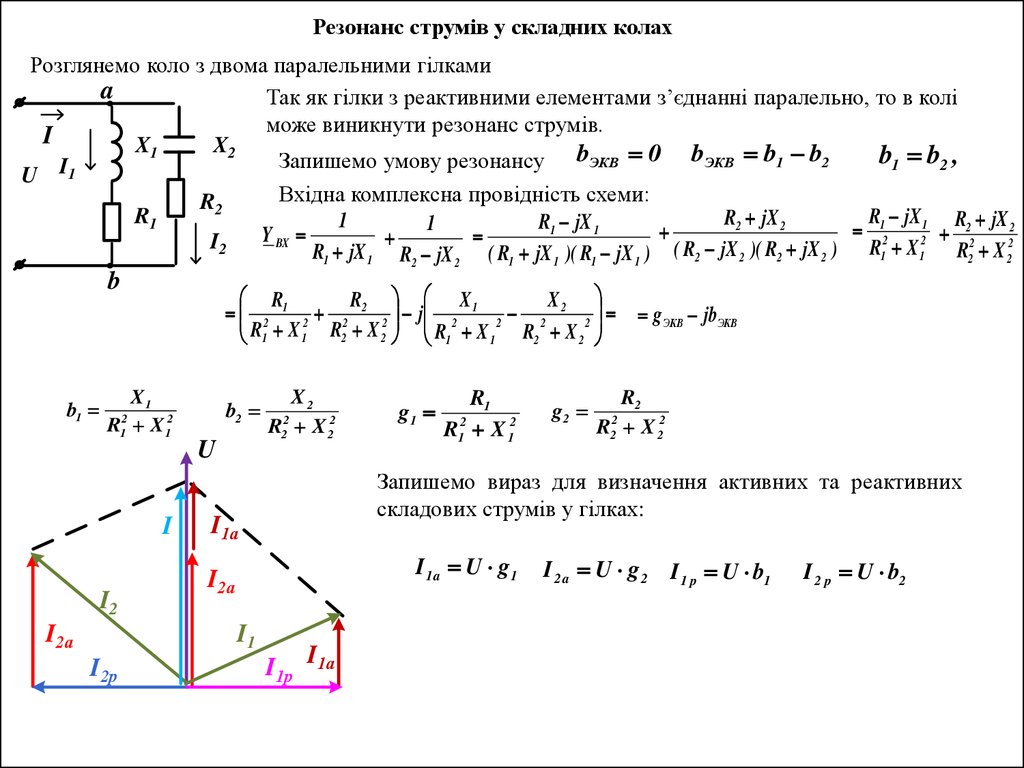
Резонанс струмів у складних колах
Розглянемо коло з двома паралельними гілками
a
Так як гілки з реактивними елементами з’єднанні паралельно, то в колі
може виникнути резонанс струмів.
I
X1
X2
b1 b2 ,
Запишемо умову резонансу bЭКВ 0 bЭКВ b1 b2
I
1
U
Вхідна комплексна провідність схеми:
R2
R1 jX 1 R2 jX 2
R1
R2 jX 2
1
R1 jX 1
1
Y
2
2
BX
2
2
I2
R1 jX 1 R2 jX 2 ( R1 jX 1 )( R1 jX 1 ) ( R2 jX 2 )( R2 jX 2 ) R1 X 1 R2 X 2
b
b1
R
R X
X
2 1 2 2 2 2 j 2 1 2 2 2 2
R1 X 1 R2 X 2 R1 X 1 R2 X 2
X1
R12 X 12
b2
U
I
I2
I2а
X2
R22 X 22
R1
R X 12
2
1
g2
R2
R X 22
2
2
Запишемо вираз для визначення активних та реактивних
складових струмів у гілках:
I1а
I 1a U g1
I2а
I1
I2р
g1
g ЭКВ jbЭКВ
I1р
I1а
I 2 a U g 2 I 1 p U b1
I 2 p U b2

27.

Індуктивно зв’язані електричні кола
i1
i2
w1 w2
Ф11
Ф1
Ф21
Ф12
Ф22
Ф2
Якщо магнітне поле, яке створюється однією з котушок, перетинає
площину витків (зчеплене з витками) другої котушки, то такі котушки
прийнято називати індуктивно зв’язаними
Ф11 — частина магнітного потоку, яке створюється струмом i1, який
зчеплений лише з витками котушки w1.
Ф22 — частина магнітного потоку, яке створюється струмом i2, який
зчеплений лише з витками котушки w2.
Ф12 — частина магнітного потоку, який створюється струмом i1, який зчеплений з витками обох
котушок (взаємний потік).
Ф21 — частина магнітного потоку, який створюється струмом i2, який зчеплений з витками обох
котушок (взаємний потік).
Ф1 = Ф11 + Ф12 — сумарний магнітний потік, який створюється струмом i1.
Ф2 = Ф22 + Ф21 — сумарний магнітний потік, який створюється струмом i2.
Власною індуктивністю котушки L називається відношення її власного потокозчеплення струму
в ній:
L1
1
i1
Ф1 w1
i1
L2
2
i2
Ф2 w2
i2
Взаємною індуктивністю М називається відношення взаємного
потокозчеплення 2-ї котушки до струму в 1-й або навпаки:
Ступінь магнітного зв’язку між котушками характеризується
коефіцієнтом зв’язку:
Ф12 w2
Ф w
21 1 .
i1
i2
M
kсв
L1 L2
M

28.

При протіканні одночасно за обома котушкам постійних струмів i1 та i2 їх власні й взаємні
магнітні потоки можуть збігатися за напрямком (співнапрямленні), й тоді виникає посилення
магнітного поля, або можуть не збігатися (протилежно напрямленні), тоді виникає послаблення
магнітного поля.
Якщо при обраних напрямках струмів в котушках їх власні й взаємні потоки збігаються, то
такі напрямки струмів прийнято називати співнапрямленними (в протилежному випадку
зустрічними).
Виводи котушок, відносно яких співнапрямленні струми орієнтовані однаково (наприклад,
вводу в котушку), називаються однойменними або однополярними.
1
1
M
2
2
На схемах електричних кіл однойменні виводи котушок позначаються
однаковими символьними знаками (зірочка, точка), а наявність взаємного
магнітного зв’язку дугою зі стрілками на кінцях
При протіканні по котушкам змінних синусоїдальних струмів у них за законом
електромагнітної індукції будуть наводитися одночасно ЕРС самоіндукції та ЕРС взаємної
індукції, які в сумі врівноважать прикладені до котушок напруги:
диференціальна форма рівнянь 2-го закону Кірхгофа
u1 e1сам e1вз L1
di
di1
M 2
dt
dt
u2 e2 сам e2 вз L2
комплексна форма рівнянь 2-го закону Кірхгофа
U 1 I 1 jX 1 I 2 jX м
U 2 I 2 jX 2 I 1 jX м
X 1 L1 , X 2 L2 - індуктивні опори котушок індуктивності,
X М М
- опір взаємоіндукції.
di 2
di
M 1
dt
dt

29.

Послідовне з’єднання індуктивно зв’язаних котушок
M
Нехай дві індуктивно зв’язані котушки (R1, L1, R2, L2, M)
з’єднанні послідовно з джерелом напруги U
При співнапрямленному включенні власні й взаємні
L
L
I R1
R2
магнітні потоки будуть складуватися, а при зустрічному
1
2
— відніматись.
U1
U2
За другим законом Кірхгофа:
U
di
di M di
di
u u1 u2 iR1 L1 M iR2 L2
диференціальна форма,
dt
dt
dt
dt
комплексна форма U U 1 U 2 I R1 I jX 1 I jX M I R2 I jX 2 I jX M
IXМ
U2
U1
IXМ
IR1
IX2
IX2
IR2
Z ЭКВ
IXМ
U
З комплексного рівняння слідує:
U
X ЭКВ .СОГЛ X ЭКВ .ВСТР
4
I
RЭКВ jX ЭКВ
IR2 X ЭКВ .ВСТР X 1 X 2 2 X M
IXМ
XM
( R1 R2 ) j( X 1 X 2 2 X M )
X ЭКВ .СОГЛ X 1 X 2 2 X M
U1
IR1
R ЭКВ R1 R2 X X 1 X 2 2 X M ,
ЭКВ
U2
IX1
I
U
IX1
M
I
Розв’язуючи разом останні
рівняння, отримаємо:
LЭКВ .СОГЛ LЭКВ .ВСТР
.
4

30.

Паралельне з’єднання індуктивно зв’язаних котушок
I
R1
U
I2
M
R2
I1
L1
L2
Дві котушки з опорами R1 та R2, індуктивностями L1 та L2 й взаємною
індуктивністю М з’єднанні паралельно, причому однойменні виводи
приєднанні до одного й того ж вузла
Для обраних додатних напрямків струмів за законами Кірхгофа
запишемо наступні вирази:
I I1 I2 ,
U I 1 Z 1 I 2 Z M ,
U I 1 Z M I 2 Z 2 .
Z 1 R1 j L1
Z 2 R2 j L2 Z M j M
У цих рівняннях комплексні напруги
I 1 Z M I 2 Z M взяті зі знаком плюс,
так як додатні напрямки струмів у гілках відносно однойменних виводів однакові.
Розв’язав рівняння, отримаємо вхідний опір кола
Z ВХ
Z Z Z M
1 2
.
I Z 1 Z 2 2Z M
U
2

31.

1
I1
R1
L1
Еквівалентна заміна індуктивно зв’язаних кіл
Часто для спрощення розрахунків частину схеми
U
2
замінюють еквівалентною схемою без індуктивних
M
I2
зв’язків.
R2
L2
Тут струми й однаково орієнтовані відносно
однойменних затискачів, тому включення котушок
узгоджене.
I
3
3
Запишемо вирази
U 13 I 1 Z 1 I 2 Z M ,
Z 1 R1 j L1 Z 2 R2 j L2 Z M j M
Перетворимо рівняння для напруг між виводами 1–3 й 2–3:
U 13 I 1 Z 1 I 2 Z M , додамо доданок
( I 1 Z M
U 23 I 1 Z M I 2 Z 2 . додамо доданок
)
( I 2 Z M )
Після перетворень отримаємо наступні вирази:
U 13 I 1 ( Z 1 Z M ) ( I 1 I 2 ) Z M ,
U 23 I 2 ( Z 2 Z M ) ( I 1 I 2 ) Z M ,
Підставимо третій струм у рівняння для напруг:
U 13 I 1 ( Z 1 Z M ) I 3 Z M ,
U 23 I 1 Z M I 2 Z 2 . I 3 I 1 I 2 ,
U 23 I 2 ( Z 2 Z M ) I 3 Z M .
Зобразимо схему, відповідно перетвореним рівнянням.

32.

U
1
I1
2
I2
R1
Х1
-ХМ
Х2
-ХМ
R2
ХМ
I3
3
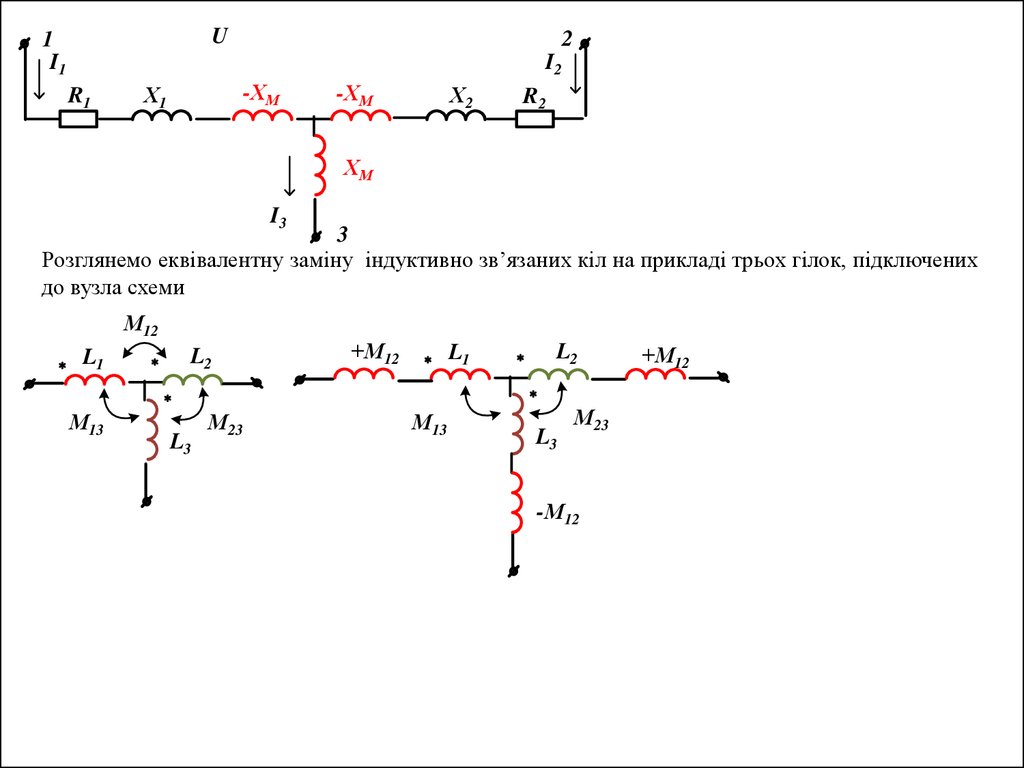
Розглянемо еквівалентну заміну індуктивно зв’язаних кіл на прикладі трьох гілок, підключених
до вузла схеми
М12
L1
L2
+М12
L3
L2
М13
L1
М23
М13
L3
М23
-М12
+М12

33.

+М13
+М12
L1
L2
+М12
-М13
+М12
-М13
М23
L3
-М12
+М13
+М23
+М13
+М12
L1
L2
L3
-М12
+М13
-М23
-М23

34.

R1
I1
M12
Складне коло з індуктивно зв’язаними котушками
Запишемо систему рівнянь за законами Кірхгофа в диференціальній
формі
i1 i 2 i 3 0
X3
di1
di
di
di
di
R2
i1 R1 i2 R2 L2
R3
L2
L1
M23
e2
e1
M 23
dt
1
3
L1
M 12
2
Комплексна форма запису системи рівнянь:
L3
I2
M 12
e1 e2
dt
dt
dt
dt
1
di2
di
di
di
di
M 23 3 M 12 1 e2
i2 R2 i3 dt i 3 R3 L3 3 M 23 2 L2
C
dt
dt
dt
dt
dt
2
I1 I 2 I 3 0
I3
I 1 R1 I 2 R2 jX 2 I 2 jX M 12 I 1 jX M 23 I 3 jX 1 I 1 jX M 12 I 2 E 1 E 2
I 2 R2 jX C 3 I 3 jX 3 I 3 jX M 23 I 2 jX 2 I 2 jX M 23 I 2 jX M 12 I 1 E 2
Метод контурних струмів Z 11 I 11 Z 12 I 22 E 11
Z 21 I 11 Z 22 I 22 E 22
Z 11 R1 R2 jX 1 jX 2 2 jX M 12
Z 22 R3 R2 jX C 3 jX 3 jX 2 2 jX M 23
Z 12 Z 21 ( R2 jX 2 jX M 12 jX M 23 ).
I 1 I 11
I 2 I 11 I 22
I 3 I 22 .
E 11 E 1 E 2
E 22 E 2

35.

Обчислення складного кола
Обчислення опорів гілок:
R1
I1
e1
X4
R3
L2
L1
I2
1
1
C 3 2 fC 3
Z 1 R1 jX 1
L3
e2
X 2 L2 2 fL2 X 3 L3 2 fL3
X 1 L1 2 fL1
С3
R2
E1
I3
E2
Z 2 R2 jX 2
Z 3 R3 jX 3 jX 4
E 1 m j
E
E
e
1m cos 1 j 1m sin 1 E1a jE1 p
2
2
2
1
E 2 m j
E
E
e
2 m cos 2 j 2 m sin 2 E 2 a jE 2 p
2
2
2
2
Метод контурних струмів
Z 11 I 11 Z 12 I 22 E 11
Z 21 I 11 Z 22 I 22 E 22
Z 11 Z 1 Z 2
E 11 E 1 E 2
Z 22 Z 3 Z 2 Z 12 Z 21 Z 2
E 22 E 2
I 1 I 11
I 2 I 11 I 22
I 3 I 22 .

36.

Обчислення складного кола
а
R1
Метод двох вузлів
I1
С3
R2
R3
L2
L1
e1
L3
e2
I2
I3
U ab
Y1
E 1 Y1 E 2 Y2
Y1 Y2 Y3
1
1
1
, Y2
, Y3
Z1
Z2
Z3
b
- комплексні
провідності гілок
струми гілок
I 1 ( U ab E 1 )Y1 , I 2 ( U ab E 2 )Y2 , I 3 U ab Y3
Потужність джерел
E 1 I 1 E 2 I 2 Pист jQист
Потужність споживачів
Pпотр I 12 R1 I 22 R2 I 32 R3
Qпотр I 12 X 1 I 22 X 2 I 32 ( X 3 X 4 )