Двухполюсники. Реактивные двухполюсники

1.

Двухполюсники

2.

Цепи с сосредоточенными параметрами и рассредоточенными
параметрами
Если индуктивность сосредоточена в L
элементах, а емкость в С, потери в R и
Lc<<λр , то это будет цепь
сосредоточенными параметрами.
Lc - длина соединительных проводов.
λр – длина волны.
Главным свойством таких цепей: Если
привести сечения в разных областях
проводов, то ток в любом сечении один и
тот же.
К цепям с распределенными параметрами
относятся: электрическая линия,
протяженностью L≈λ. Параметры R, L, C, G –
распределении по всей длине

3.

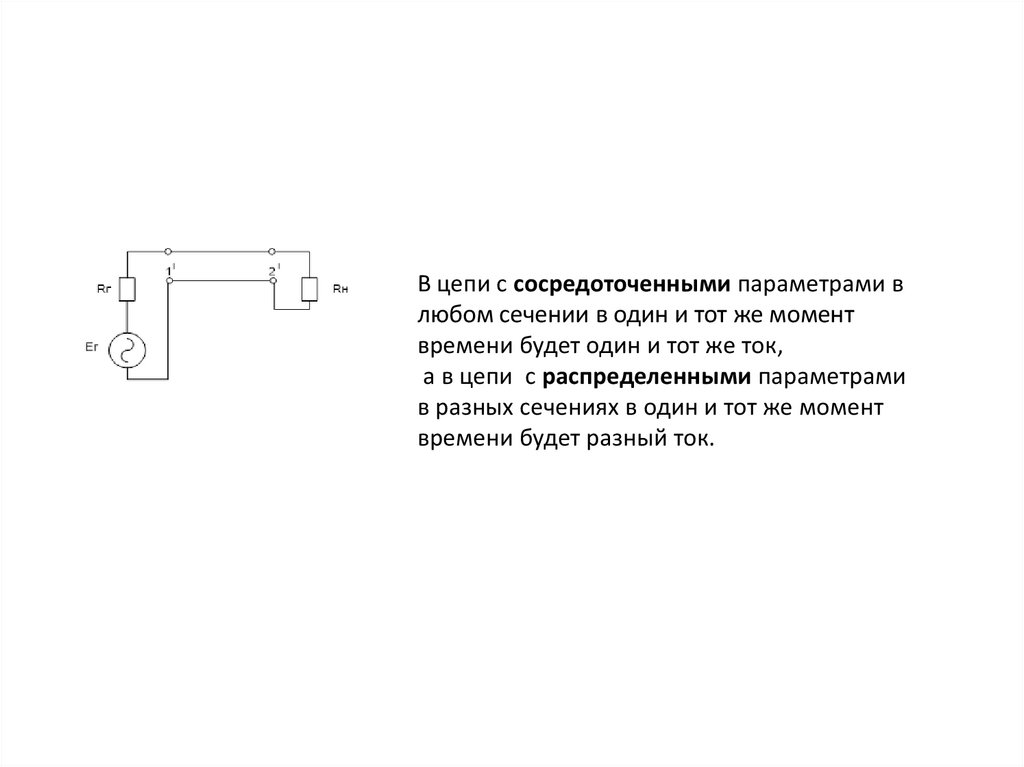
В цепи с сосредоточенными параметрами в
любом сечении в один и тот же момент
времени будет один и тот же ток,
а в цепи с распределенными параметрами
в разных сечениях в один и тот же момент
времени будет разный ток.

4.

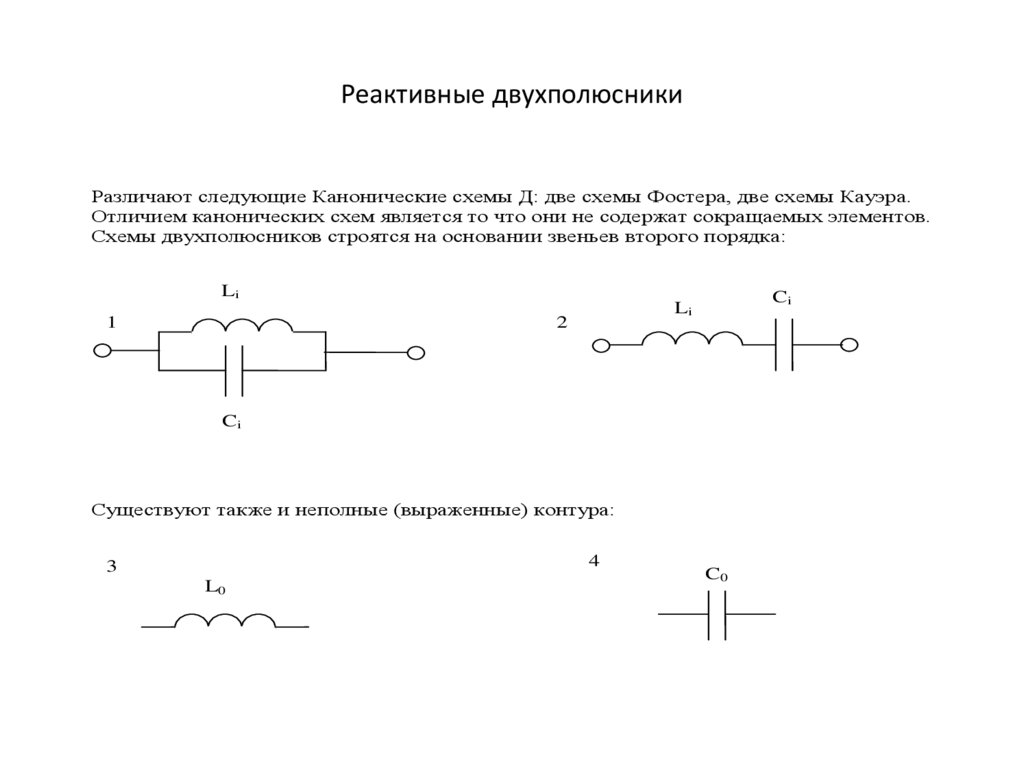
Реактивные двухполюсники
Различают следующие Канонические схемы Д: две схемы Фостера, две схемы Кауэра.
Отличием канонических схем является то что они не содержат сокращаемых элементов.
Схемы двухполюсников строятся на основании звеньев второго порядка:
Li
2
1
Ci
Li
Ci
Существуют также и неполные (выраженные) контура:
4
3
L0
C0

5.

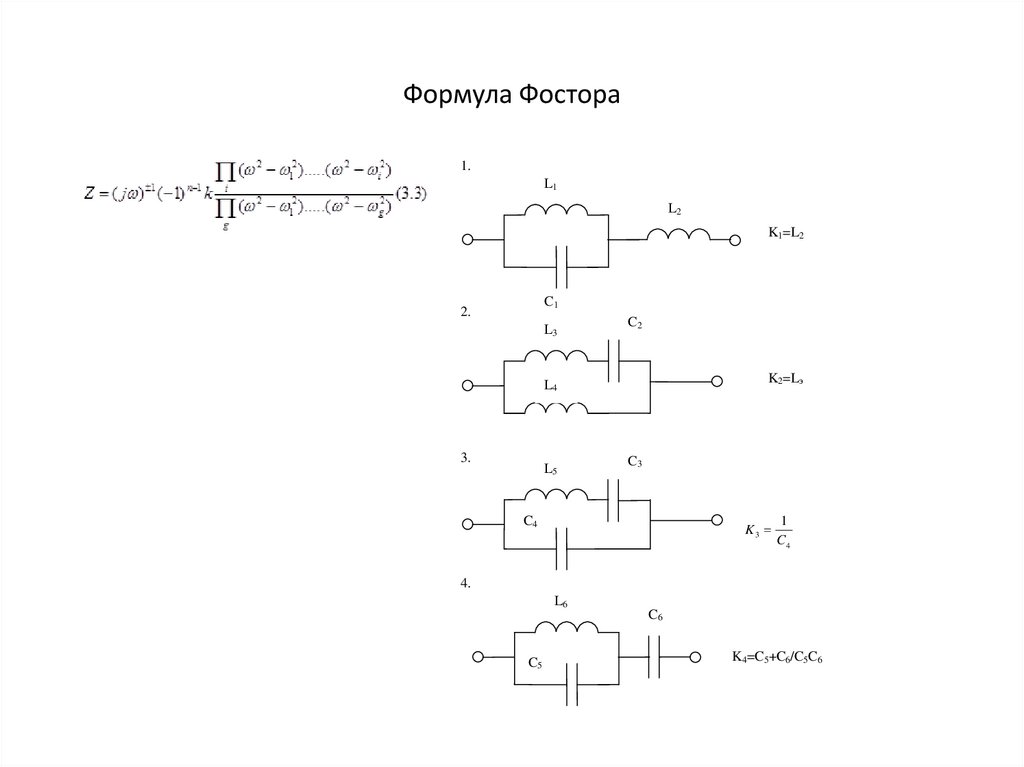
Формула Фостора
1.
L1
L2
K1=L2
C1
2.
L3
C2
K2=Lэ
L4
3.
L5
C3
C4
K3
1
C4
4.
L6
C5
C6
K4=C5+C6/C5C6

6.

Обратные Двухполюсники
Обратные двухполюсники – такие Д у которых произведение сопротивлений
Z1*Z2 на всех частотах величина постоянна Z1*Z2=R2=const (3.4)

7.

Эквивалентный двухполюсники
2
2
2 32(1)
L3 * L4 3( 2)
Z1 Z 2 j L2 2
j
22(1)
L3 L4 2 22( 2)
3(1) 3( 2 )
2 (1) 2 ( 2 ) (3.6) раскроем эту систему:
k1 k 2
L1 L2
1
L1 * L2 * C1 L3C 2
1
1
L1C1 ( L3 L4 ) * C 2
LL
L2 3 4
L3 L4

8.

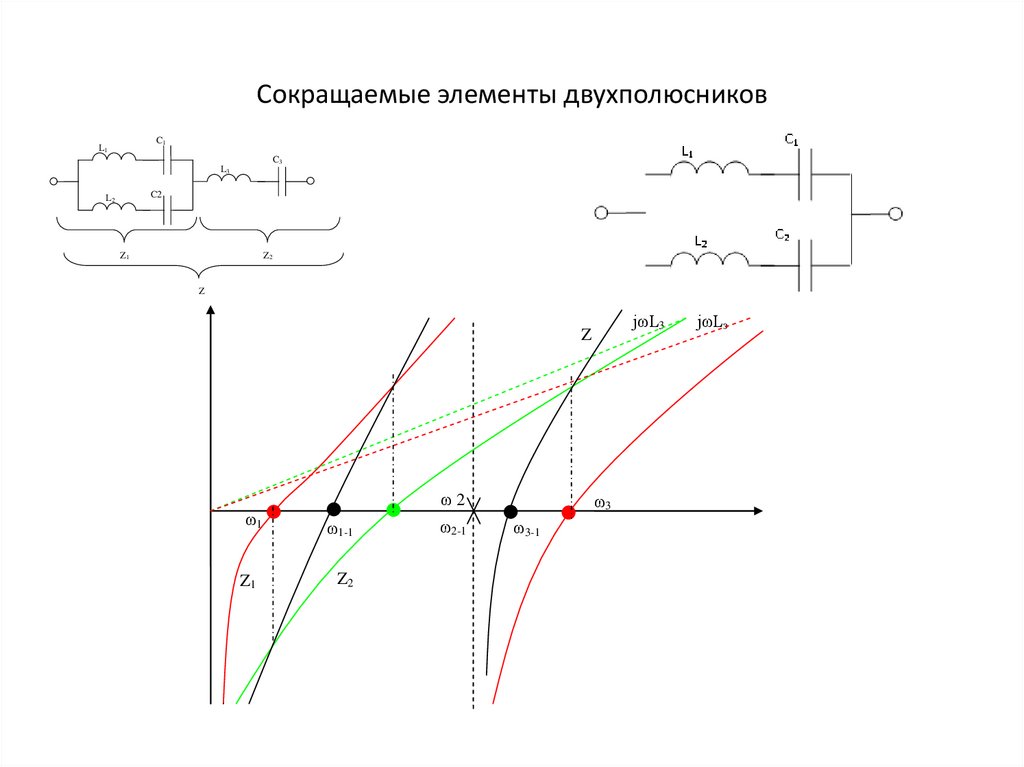
Сокращаемые элементы двухполюсников
C1
L1
C3
L3
C2
L2
Z1
Z2
Z
jωL3
Z
ω2
ω1
Z1
ω1-1
Z2
ω2-1
ω3
ω3-1
jωLэ

9.

Синтез двухполюсников
Свойства входных функций
Критерии физической реализуемости
Предположим, что an ф-ии входного типа тогда:
ni
n 1i
i
nU
U
a
....
a
a
i
b
.... b1
b0U
n 1
0
n
n
n 1
n
t
t
t
t
t
Или в операторной форме:
(an p n an 1 p n 1 ..... a1 p a0 ) I ( P) (bm p m ... b1 p b0 )U ( P) (3.7)
an
A(P)
B(P)
A(P), B(P)- полиномы
Z(P) можно представить в виде:
Z ( P)
U ( P) A( P) an p n ... a1 p a0
(3.8)
I ( P) B( P) bm p m ... b1 p b0
Каким условиям должна удовлетворять функциям 4.10, чтобы быть реализованной в виде
схемы.
Z ( P) pLЭ
При ω→∞ чисто реактивное сопротивление ведет себя:
1
Z ( P) pC
Э
an p n m
bm
1). Высшая степень переменной числителя и высшая степень переменной знаменателя
отличаются на 1
a 1
a
1
m n n
m n n P LЭ
bm P
Cэ
bm
2). Критерии :все коэффициенты полиномов положительны и вещественны
3). Нули и полюса Z(P) находятся в левой полуплоскости комплексной частоты.
4). Нули и полюса Z(P) должны быть некратными, простыми.
5). Нули и полюса строго чередубтся.
Следовательно lim p Z ( P) lim p

10.

Синтез по Фостеру.
Первая формула
Дано аналитическое выражение Z(jω) – Z(P)
Требуется определить схему и величины элементов.
Первое : проверяем выражение по критериям физической реализуемости .
Второе: Задаемся следующей схемой:
L1
C1
Li
Ci
L0
C0
Третье: Решаем заданное выражение
A( P)
Z ( P)
B( P) , решая уравнение A(P)=0, находим нули решая B(P)=0.
Находим полюса Z(P).
Для определения величин элементов моно и не находить нули Z(P), достаточно найти
полюса, т.к. такая функция полностью определяется вычитаниями полюсов.
U ( P) A( P) an p n ... a1 p a0
Z ( P)
(3.9)
Величина Z(P) при P→∞ стремится к pL0.
I ( P) B( P) bm p m ... b1 p b0
Если от заданного аналитического выражения определить limP→∞ Z ( P ) то этот дает L0 в
P
полюсе бесконечности.
Со определяет поведение Z(P) при P→0. Необходимость нахождения L0 и Со обявлялась
в пункте (3.1.1).
P 2 i2 1
1
1
2
При lim p j i Z ( P)
(3.10) i L C Li 2 C (3.11)
P
C
i i
i
i
i

11.

Синтез по второй формуле Фостера
1). Проверяем выражение по критериям физической реализуемости.
C1
L1
Li
Ci
L0
C0
2). Задаемся схемой:
3). В данном случае удобнее работать с проводимостью:
B( P)
1
1
1
P
Y ( P)
PC0
(3.12) Y ( P)
2
2
Z ( P)
PL0
Li P i
A( P)
При A(P)=0 – находим все полюса Z(P)
Y ( P)
Если в точке ω=0 есть полюс то есть С0 lim p
P C0 (3.13)
1
(3.14)
При ω→0 lim P 0 Y ( P) * P
L0
P 2 i2 1
lim P j i Y ( P) *
(3.15)
P Li

12.

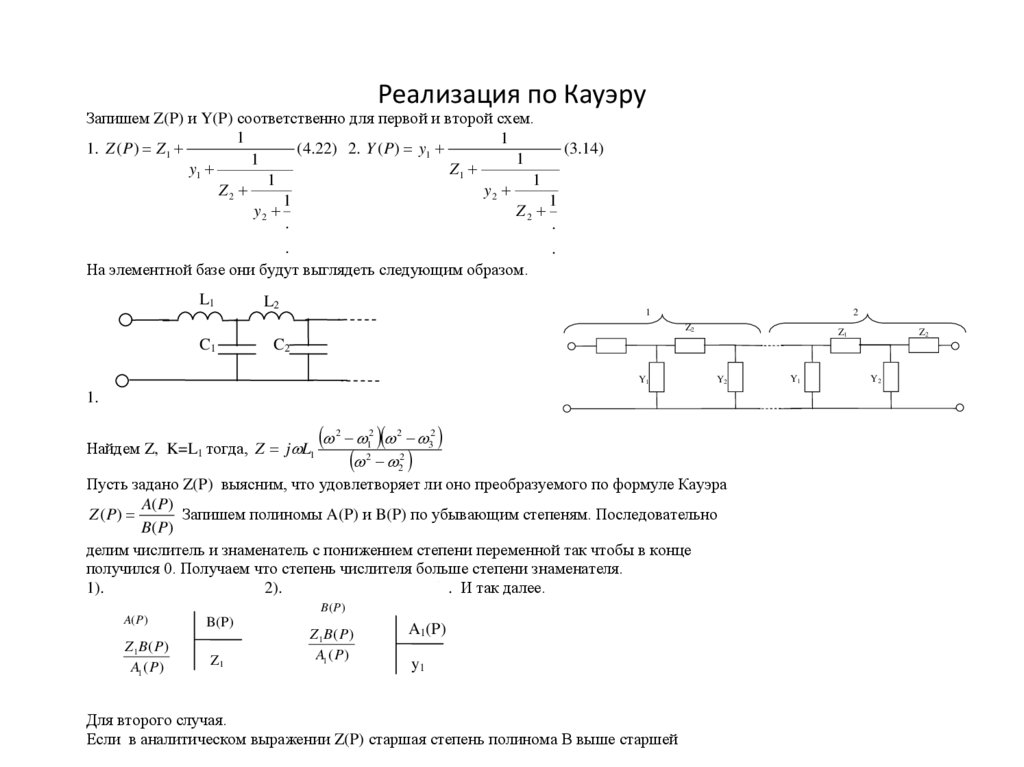
Реализация по Кауэру
Запишем Z(P) и Y(P) соответственно для первой и второй схем.
1
1
1. Z ( P) Z1
(4.22) 2. Y ( P) y1
(3.14)
1
1
Z1
y1
1
1
Z2
y2
1
1
y2
Z2
.
.
.
.
На элементной базе они будут выглядеть следующим образом.
L1
L2
1
2
Z2
C1
Z1
Y1
Y2
1.
12 2 32
2 22
Пусть задано Z(P) выясним, что удовлетворяет ли оно преобразуемого по формуле Кауэра
A( P)
Z ( P)
Запишем полиномы A(P) и B(P) по убывающим степеням. Последовательно
B( P)
делим числитель и знаменатель с понижением степени переменной так чтобы в конце
получился 0. Получаем что степень числителя больше степени знаменателя.
1).
2).
3). И так далее.
Найдем Z, K=L1 тогда, Z j L1
2
B(P)
A(P)
Z1 B ( P )
A1 ( P )
B(P)
Z1
Z2
C2
Z1 B ( P )
A1 ( P )
B(P)
B(P)
A1(P)
Z1
yZ11
Для второго случая.
Если в аналитическом выражении Z(P) старшая степень полинома В выше старшей
Y1
Y2

13.

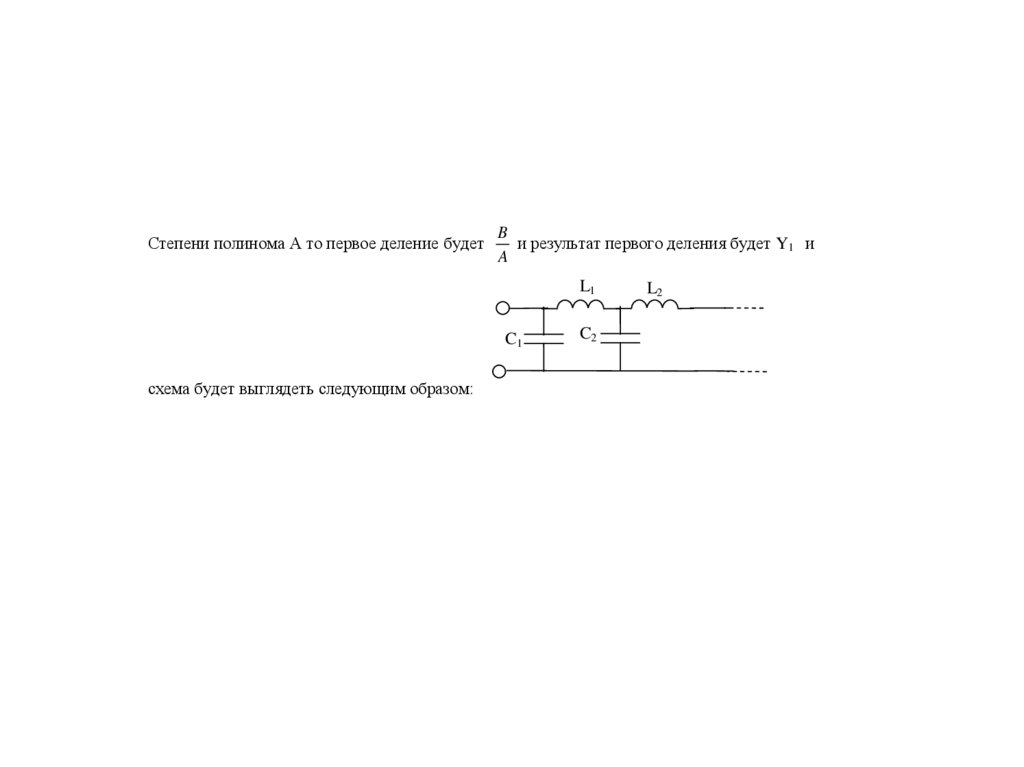
Степени полинома А то первое деление будет
B
и результат первого деления будет Y1 и
A
L1
C1
схема будет выглядеть следующим образом:
C2
L2

14.

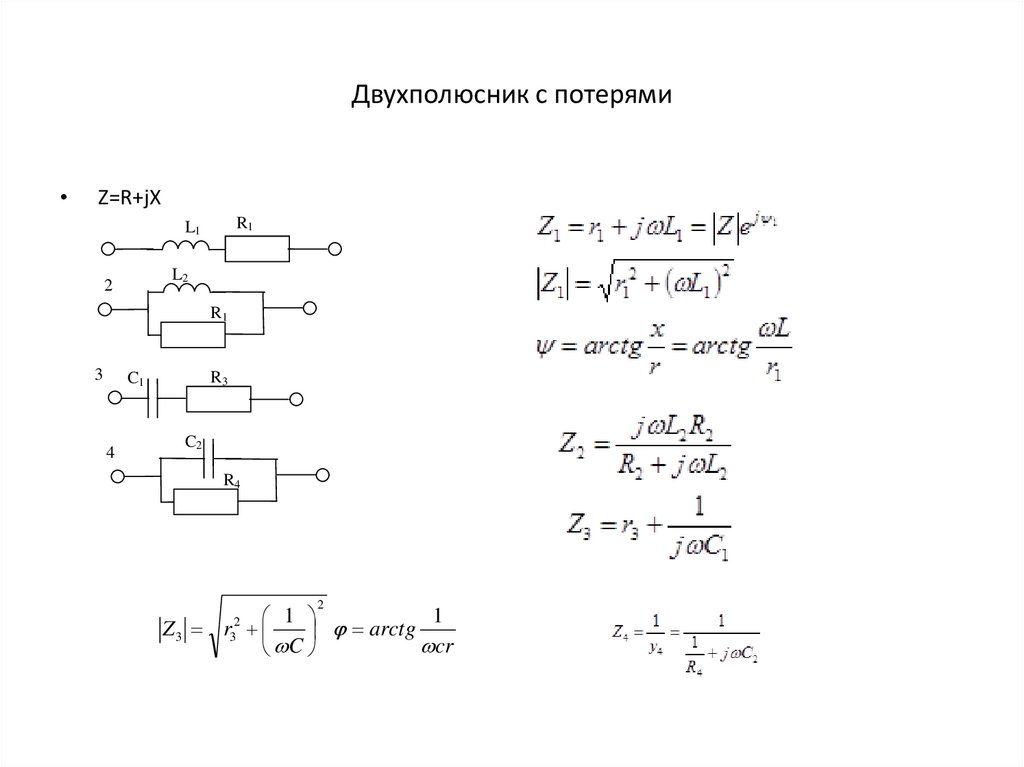
Двухполюсник с потерями
Z=R+jX
R1
L1
L2
2
R1
3
R3
C1
4
C2
R4
2
1
1
Z3 r
arctg
cr
C
2
3

15.

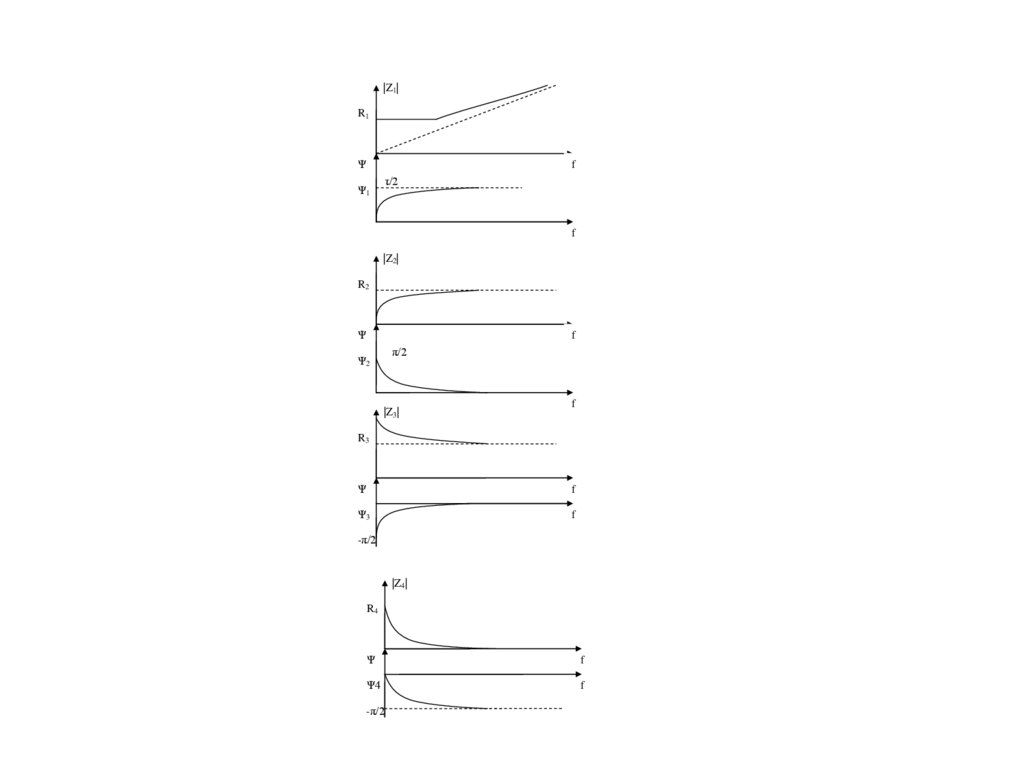
|Z1|
R1
Ψ
f
Ψ1
π/2
f
|Z2|
R2
Ψ
f
π/2
Ψ2
|Z3|
f
R3
Ψ
f
Ψ3
f
-π/2
|Z4|
R4
Ψ
f
Ψ4
f
-π/2

16.

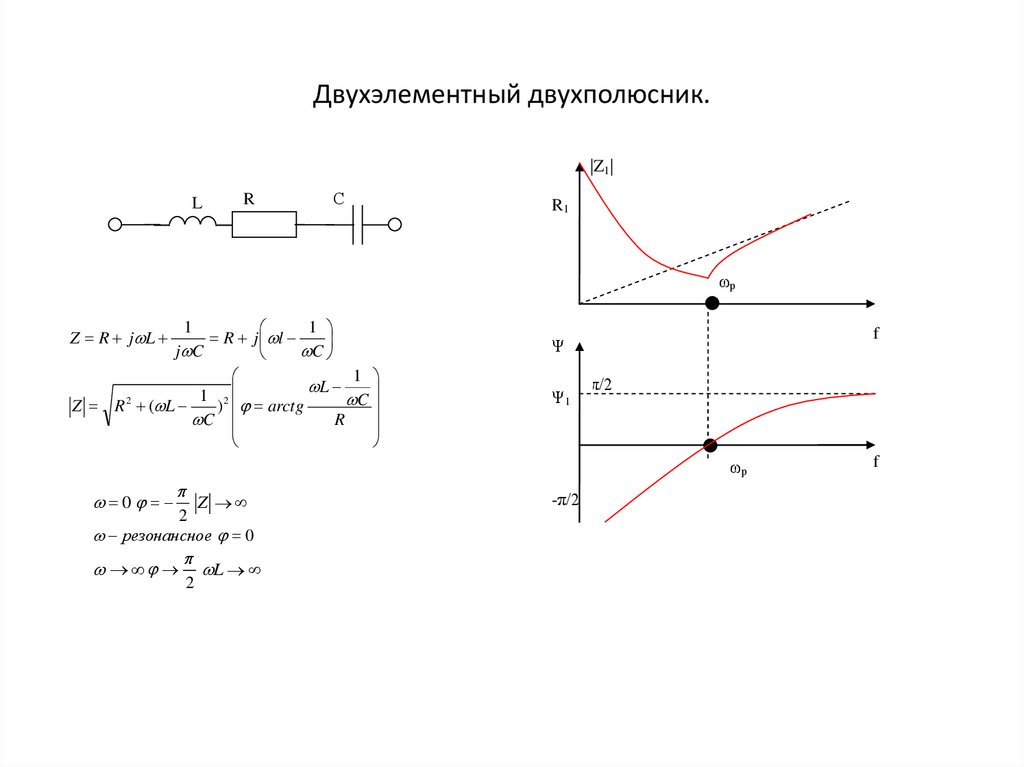
Двухэлементный двухполюсник.
|Z1|
L
R
С
R1
ωр
1
1
R j l
j C
C
1
L
1
C
Z R 2 ( L
) 2 arctg
C
R
Z R j L
f
Ψ
Ψ1
π/2
ωр
0
Z
2
резонансное 0
2
L
-π/2
f

17.

R1
L
R2
С
R2
1
j
1
1
R1
R2
j L
C
y
2
2
2
2
R1 j L R 1
R1 ( L)
R
(
L
)
1
1
1
2
2
2
R
R
2
2
j C
C
C
Re(y)
Im(y)
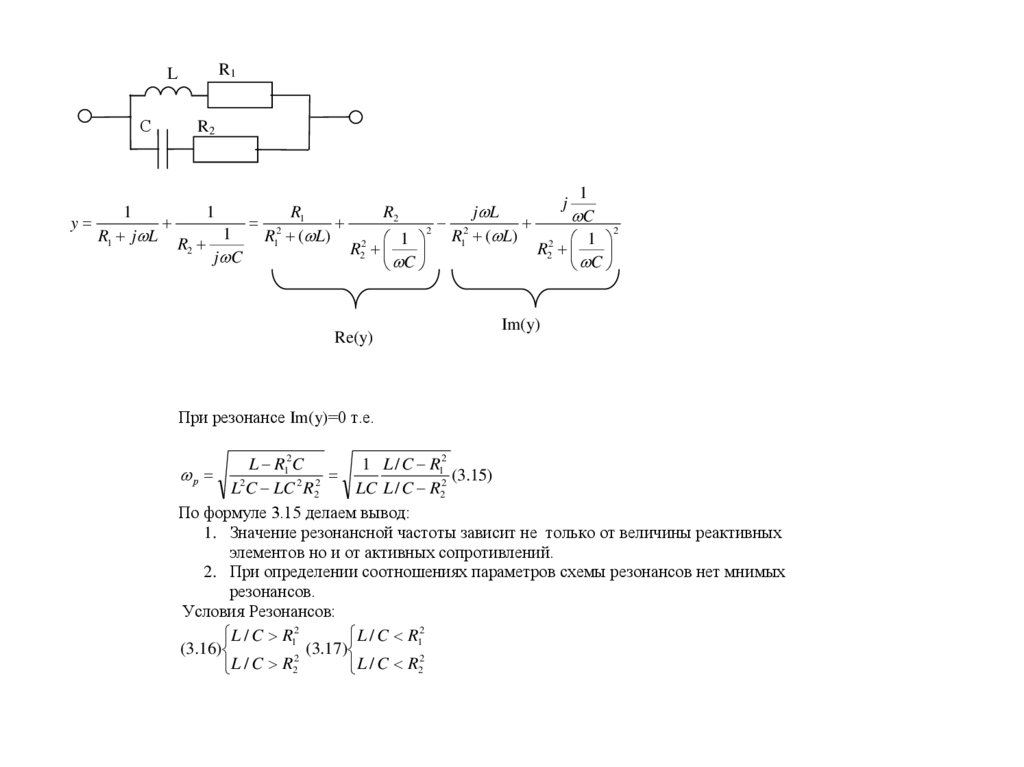
При резонансе Im(y)=0 т.е.
L R12C
1 L / C R12
(3.15)
LC L / C R22
L2C LC 2 R22
По формуле 3.15 делаем вывод:
1. Значение резонансной частоты зависит не только от величины реактивных
элементов но и от активных сопротивлений.
2. При определении соотношениях параметров схемы резонансов нет мнимых
резонансов.
Условия Резонансов:
L / C R12
L / C R12
(3.16)
(
3
.
17
)
L / C R22
L / C R22
р

18.

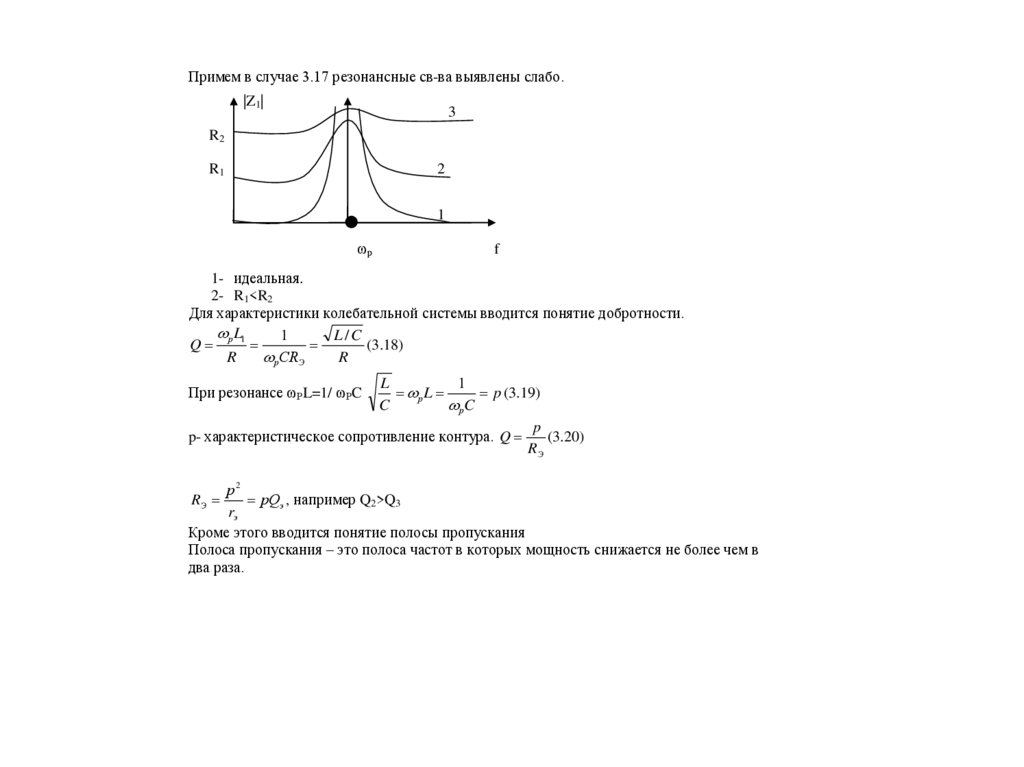
Примем в случае 3.17 резонансные св-ва выявлены слабо.
|Z1|
3
R2
R1
2
1
ωр
f
1- идеальная.
2- R1<R2
Для характеристики колебательной системы вводится понятие добротности.
L
1
L/C
(3.18)
Q р 1
R
рСRЭ
R
L
1
р L
p (3.19)
C
рC
p
(3.20)
p- характеристическое сопротивление контура. Q
RЭ
При резонансе ωРL=1/ ωРC
р2
рQэ , например Q2>Q3
rэ
Кроме этого вводится понятие полосы пропускания
Полоса пропускания – это полоса частот в которых мощность снижается не более чем в
два раза.
RЭ

19.

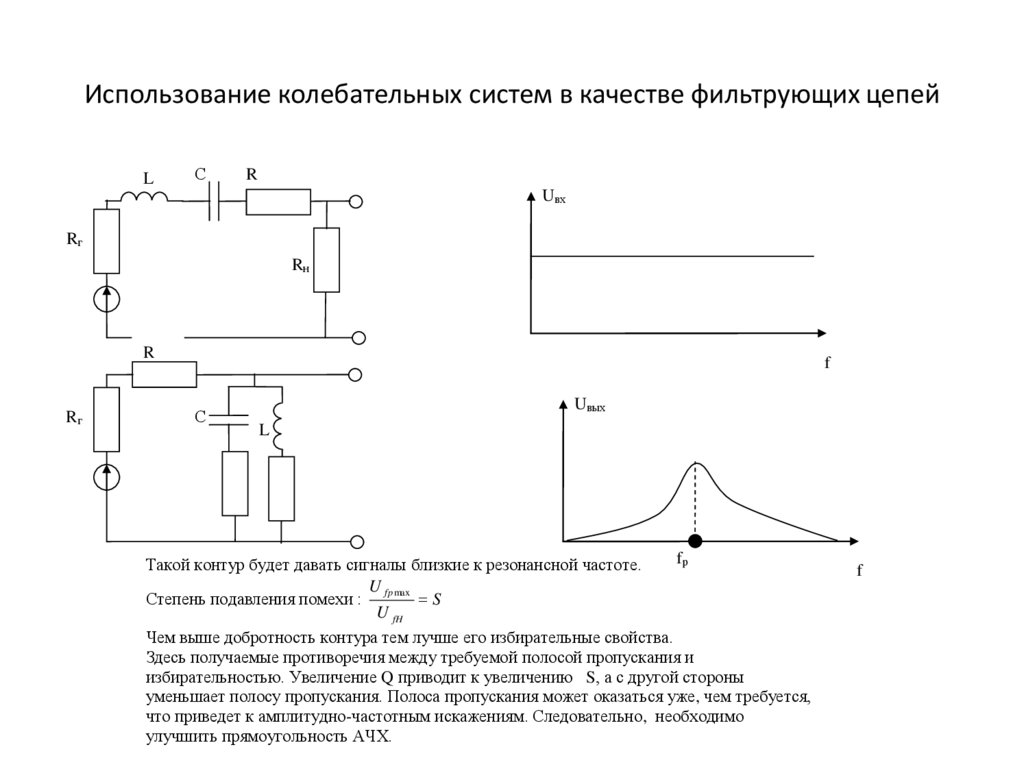
Использование колебательных систем в качестве фильтрующих цепей
L
С
R
Uвх
Rг
Rн
R
Rг
f
С
Uвых
L
С
fр
Такой контур будет давать сигналы близкие к резонансной частоте.
U fp max
S
Степень подавления помехи :
U fH
Чем выше добротность контура тем лучше его избирательные свойства.
Здесь получаемые противоречия между требуемой полосой пропускания и
избирательностью. Увеличение Q приводит к увеличению S, а с другой стороны
уменьшает полосу пропускания. Полоса пропускания может оказаться уже, чем требуется,
что приведет к амплитудно-частотным искажениям. Следовательно, необходимо
улучшить прямоугольность АЧХ.
f