Идеальный газ

1.

ГЛАВА II. МОЛЕКУЛЯРНАЯ
ФИЗИКА И
ТЕРМОДИНАМИКА
§2. Идеальный газ
О. И. Лубенченко
НИУ МЭИ
Кафедра физики им. В. А. Фабриканта
2020

2.

§2. Идеальный газ
2
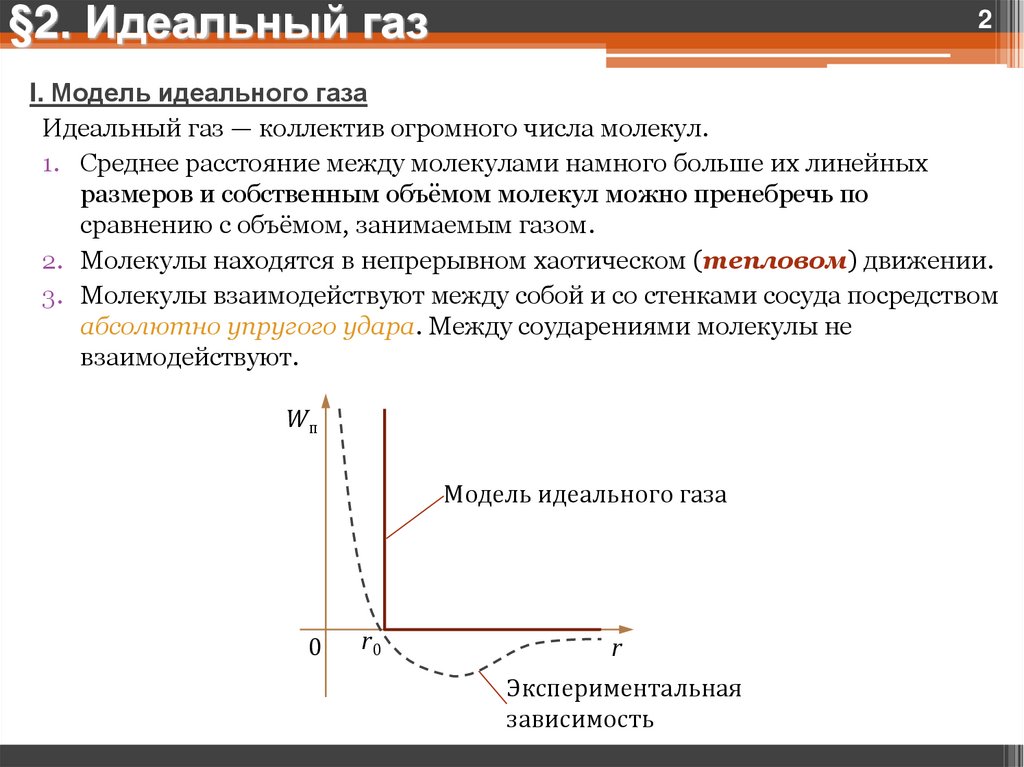
I. Модель идеального газа
Идеальный газ — коллектив огромного числа молекул.
1. Среднее расстояние между молекулами намного больше их линейных
размеров и собственным объёмом молекул можно пренебречь по
сравнению с объёмом, занимаемым газом.
2. Молекулы находятся в непрерывном хаотическом (тепловом) движении.
3. Молекулы взаимодействуют между собой и со стенками сосуда посредством
абсолютно упругого удара. Между соударениями молекулы не
взаимодействуют.
Wп
Модель идеального газа
0
r0
r
Экспериментальная
зависимость

3.

§2. Идеальный газ
3
II. Уравнение состояния идеального газа. Газовые законы
Уравнение состояния идеального газа:
pV
const
T
Частные случаи (газовые законы):
1. T = const: pV const — закон Бойля-Мариотта
V
2. p = const: const — закон Гей-Люссака
T
p
const — закон Шарля
3. V = const:
T
m
pV RT — уравнение Менделеева-Клапейрона
μ
R 8,31
ν
m
μ
Дж
— универсальная газовая постоянная
моль К
k
pV νRT
N
RT NkT
NA

4.

§2. Идеальный газ
k
4
R
Дж
— постоянная Больцмана
1,38 10 23
NA
К
Концентрация молекул — ФВ — характеристика макросистемы, равная
числу частиц в единичном объёме:
n м 3
N
n
V
p
N
kT
V
p nkT
Закон Дальтона: давление смеси газов равно сумме парциальных
давлений компонент смеси:
p pi
Доказательство
pi ni kT
N
N Ni
n
i ni
V
V
V
p n kT kT n nkT
i
Нормальные условия: p0 = 1,01·105 Па; T0 = 273 К
i
i

5.

§2. Идеальный газ
5
III. Основное уравнение МКТ
Рассмотрим равновесный идеальный газ, состоящий из одинаковых молекул
массой m0. Все молекулы имеют разные по модулю и направлению скорости.
Давление газа обусловлено ударами молекул о стенку сосуда.
1. Удар одной молекулы
m0 v
f
*
Удар молекулы о стенку — абсолютно упругий.
v
II закон Ньютона: Δ m0 v f * τ
x
f * — сила, с которой стенка действует на молекулу
τ — время удара
x : m0 v m0 v f * τ
*
III закон Ньютона: f f
2m0 v
f
τ
f f*

6.

§2. Идеальный газ
6
2. Число ударов о стенку за время Δt >> τ
i-я скоростная группа молекул: v = (vi, vi ± Δv)
ΔS
m0
Число молекул внутри цилиндра, которые долетят до стенки
за время Δt: ΔN ni v ΔtΔS
vi
i
6
i
ni — концентрация молекул i-ой скоростной группы
viΔt
x
Коэффициент 1/6
из всех молекул 1/3 движется вдоль
оси x, из них ½ движется в направлении стенки.
3. Импульс, полученный стенкой от молекул i-ой скоростной группы за
время Δt
Fi Δt fi τ 2m0 vi ΔNi 2m0 vi
m
ni
vi ΔtΔS 2m0 vi 0 ni vi2ΔtΔS
6
3
3
Fi — модуль суммарной силы, с которой молекулы i-ой скоростной группы
действуют на участок стенки площадью ΔS
Давление молекул i-ой скоростной группы
Fi
m0ni vi2
pi
ΔS
3

7.

§2. Идеальный газ
4. Учёт давления всех скоростных групп молекул
m0
m0
2
2n
n
v
n
v
i i 3 i in
3
2
2
2
2
n
v
n
v
n
v
n
v
ii
i i
v2 1 1 2 2
n1 n2 ni
n
Закон Дальтона: p pi
n ni
m0n 2
p
v
3
v2 vкв — средняя квадратичная скорость молекулы идеального
газа
2 m0 v2
p n
3
2
— основное уравнение МКТ идеального газа
2
p n ε — основное уравнение МКТ идеального газа для энергии
3
ε — средняя кинетическая энергия поступательного движения молекулы
идеального газа
7

8.

§2. Идеальный газ
8
IV. Молекулярно-кинетический смысл абсолютной температуры
2
p n ε
3
p nkT
2
kT ε
3
3
ε kT
2
Абсолютная температура пропорциональна средней кинетической энергии
поступательного движения, приходящейся на 1 молекулу.
2
2 m0 v2
Энергетическая температура: θ kT ε
3
3 2
vкв
2 ε
m0
2 3kT
3kT
3RT
2m0
m0
μ
vкв
3RT
μ
Численная оценка
При t = 27°C (T = 300 К) для кислорода (µ = 3,2·10–2 кг/моль):
θ = 4,2·10–21 Дж
3 8,31 3 102
м
2
vкв
10
3
2,6
483
с
3,2 10 2
θ Дж