Similar presentations:
Комплексные числа и последовательности комплексных чисел. Лекция № 1
1. Лекции по теории функции комплексной переменной
2.
Лекция № 1Комплексные числа
и последовательности комплексных чисел.
1. Понятие комплексного числа.
Геометрическая интерпретация
.
Комплексные числа вошли в математику в XVI в. как корни
квадратного уравнения с отрицательным дискриминантом.
ax bx c 0
2
D b 4ac
2
D 0
D 0
b D
x1,2
2a
x1,2 ?
Как понимать? И что делать, когда дискриминант отрицателен?
3.
Вначале такие корни отбрасывались, как«невозможные», «мнимые», и появление их считалось
признаком отсутствия решения у задачи, приведшей к
квадратному уравнению
Обоснование: мнимые корни не выражают величины, так
как их нельзя сравнивать друг с другом, нельзя сказать,
какоe мнимое больше, какое меньше.
Однако позже было обнаружено, что над ними можно
производить четыре алгебраических действия, причем
сохраняются свойства, присущие действиям над
действительными числами.
Это и послужило основанием называть мнимые корни числами
(«Алгебра» итальянского инженера Р. Бомбелли, 1572 г.).
4.
Геометрическое изображение комплексныхчисел в виде точек или векторов на
плоскости было введено в 1799 г. датским
землемером К. Весселем (1745—1818) в
1806 г. французским математиком Д.
Арганом (1768—1822).
Символ i для мнимой единицы ввел в 1777 г. Л.
Эйлер (1707— 1783).
Термин «комплексное число» ввел в 1881 г.
К. Вейерштрасс (1815— 1897).
5.
Большое значение в раскрытии важной роли комплексныхчисел в математике имели работы Л. Эйлера и К. Гаусса
(1777—1855), а также теорема Даламбера (1717—1783) о
том, что любое алгебраическое уравнение n-й степени с
комплексными коэффициентами имеет n комплексных
корней.
До появления этой теоремы можно было бы ожидать, что,
подобно тому как квадратное уравнение привело к
комплексным числам, попытки решения уравнений
степеней п = 3, 4, ..., приведут к появлению все новых и
новых типов чисел.
6.
Геометрическое изображение комплексного числа как точкиили вектора на плоскости, естественно, приводит к мысли
построить дальнейшие обобщения понятия о числе.
Однако поиски числовой системы, зависящей от трех единиц: 1, i, j,
геометрически изображаемой с помощью точек или векторов 3мерного пространства, не увенчались успехом: не удавалось так
придумать правила действий над новыми «числами», чтобы
сохранились обычные их свойства.
В 1843 т. английский математик У. Гамильтон (1805—1865) показал, что
можно построить числовые системы, зависящие от четырех единиц: 1, i, j, k,
если поступиться одним свойством — переместительным законом
умножения.
7.
Гиперкомплексными числами ранга п называются «числа» видаa1 e1 a2 e2 an en
e1 , e2 ,
en
a1 , a2 ,
an
- единицы,
- действительные числа,
когда указаны правила алгебраических действий с такими «числами».
Однако К. Вейерштрасс показал, что при п > 2 нельзя сохранить все
свойства, присущие алгебраическим действиям над действительными и
комплексными числами.
Немецкий математик Ф. Фробениус (1849—1917) доказал, что, даже отказавшись от
переместительного закона умножения, можно сохранить остальные свойства
алгебраических действий дополнительно лишь для п = 4, а при n ≠ 1,2,4,
как бы не вводилось правило умножения, всегда будут пары отличных от нуля
гиперкомплексных чисел, произведение которых равно нулю.
8.
Рассмотрим плоскостьR2.
z x , y R
2
2
x R, y R. Определим z
i
y
z x, y
z
0
i z
1
2 -вектор
x y , 1
операцию сложения:
z1 x1 , y1 , z2 x2 , y2 z( x , y ) :
x x1 x2
z z1 z2
; 2
y
y
y
1
2
1
x
операцию умножения на число:
z1 z2
z x , y , R : z x , y
z2 1 1, 0 i 0, 1
0
z
x
,
y
x
1
y
i
1
базис
3
9.
Как ввести z z1 z2 , сохранив (1) и (2) ?Вектор 1– единица операции умножения.
Определим i i i 2 . Т.к. 1 i i , то полагают
2
i 1. 4
1,0
i
i
2
1,0
2
0
2
iz
z
1
1,0
0
z ( x , y ) : z i ( x 1 y i ) i y 1 x i y, x
5
10.
z1 x1 , y1 , z2 x2 , y2 Rz1 z2 ( x1 , y1 ) ( x1 , y1 )
Правило умножения
2
( x1 1 y1 i ) ( x2 1 y2 i )
x1 x2 y1 y2 1 x1 y2 x2 y1 i
x1 x2 y1 y2 ; x1 y2 x2 y1 6
2
Числовая плоскость
R называется
комплексной плоскостью C, если для ее точек
определены модули (1), операции сложения (2)
и умножения (6).
Точки комплексной плоскости С называются
комплексными числами.
11.
Действительные числа включаются вмножество комплексных чисел.
a=(a,0)-вещественное число, 0=(0, 0), 1=(1, 0),
-1=(-1, 0), ib= (0, b)-чисто мнимое число,
i =(0, 1)- мнимая единица, -i=(0, -1).
Равенство. z1 x1 , y1 , z2 x2 , y2 :
x
x
1
2
z1 z2
.
y1 y2
Алгебраическая форма записи.
z x i y Re z i Im z .
упорядоченная
пара
z ( x , y )
вещественных чисел.
12.
Комплексное сопряжение.*
*
*
z z x i y ( x , y ). Re z x , Im z y .
*
*
z z Im z z z , * *
Re z
z1 z2
2
*
*
,
* *
z1 z2 ,
z z,
2i
z1 z2
*
2
* *
z1 z2 ,
2
2
z z ( x iy )( x iy ) x y z
Деление.
*
* x x y y
z1 z1 z2 z1 z2
1 2
1 2 i y1 x2 y2 x1
2
2
2
2
z2 z2 z*2 z 2
x 2 y2
x 2 y2
2
13.
Примеры.z x iy x y i 2 xy ;
2
2
1,
i
n
i
1
i
2
n 4k
2
n 4k 1
1 i
i
*
, k 0,1,2...; i i;
n 4k 2
n 4k 3
3 4i 3 4i 2 3i 6 12
8 9
i
2 3i 2 3i 2 3i 22 32 22 32
6 17
i ;
13 13
14.
Z-2+2i
Re z=0
Комплексные числа можно изображать точками
на комплексной плоскости.
Y (Im z)
2
2+2i
1
i
X (Re z)
0
-2
-1
0
-1
-2-2i
-2
1
-i
2
Im z=0
2-2i
15.
Ziy
Arg z arg z 2 k
0
Im z
r
j
j
r
z=x+iy
z
Re z
x
-iy
z*=x-iy
16.
Модуль и аргумент комплексного числа(x,y) (r,j).
Полярные координаты
x r cos j
y r sin j
Модуль комплексного числа:
2
2
r x y z
Re z Im z
2
2
Аргумент комплексного числа:
y Im z
tg j
; j j 0 2 k; 0 j 0 0 2
x Re z
Arg z arg z 2 k;
0 arg z 0 2 Главное значение аргумента.
17.
arg z0 arg z 2
-разрез по Re z 0 - PC Soft
-разрез по Re z 0
Примеры. 0 0, arg 0 — не определен!
i 1, arg i ;
2
1 1, arg 1 ; i 1, arg i ;
2
z 2 2i , z 2 2 , arg z ;
4
1 1, arg1 0;
18.
Тригонометрическая форма записиz x i y , x r cos j , y r sin j .
z r cosj i sinj , r z , j Arg z .
формула Эйлера: j e
ij
cosj i sinj , j R.
Показательная форма записи
ij
z re
, r z , j Arg z .
Теорема. Пусть j , R, k Z , тогда
i0
ij i
i j
1) e
3) e
i j 2 k
1; 2) e e
ij
e ; 4) e
ij
e
1
ij
;
; 5) e
ij
1.
19.
Примеры.i0
1 1 cos 0 i sin 0 e ;
i
i 1 cos i sin e 2 ;
2
2
i
1 1 cos i sin e ;
i
3 i 2e 6 ;
3
i
2 2i 2 2e 4 ;
2
i
i 3 1 2e 3 ;
i
i 1 cos i sin e 2 ;
2
2
3
i
i
i
i
i 4
i 4
4
e e e e e e 4 .
20.
Вопрос.j
j
i 2
ij
2 12 1 j ?
e e
Умножение и деление в показательной форме.
ij 1
ij 2
z1 r1e , z2 r2e
,
z1 r1 i j1 j 2
i j1 j 2
e
.
z1 z2 r1r2e
,
z2 r2
ij
Формула Муавра. z re r cosj i sinj .
n
n
n inj
n
z r e
r cosj i sinj
n
r cos nj i sin nj .
cosj i sinj cos nj i sin nj
n
21.
Извлечение корня. z reij
r cosj i sinj
r cos j 2 k i sin j 2 k re
i j 2 k
;
j 2 k
i
n z n re n ,
n z n r cos j 2 k i sin j 2 k ,
n
n
k 0, 1 , n 1.
Корень n-той степени из комплексного числа
принимает n различных значений.
22.
Пример 11 i
3
3 i
2 e 4
3
9
i
3
i
3
3
4
2 e
2 e 4
2 cos i sin
4
4
3
3 2
2
2
i 2 2i .
2
2
23.
Пример 23 2 2i
1
i 2
1 / 3 3 4
8 e
k
i
e 12 , k 0;
7
i
2
e 12 , k 1;
3
i 5
i
e 4 e 4 1 i , k 2;
24.
Пример 3i0
e 1, k 0;
i
2 k
i
2
e
i , k 1;
4 1 e 4
i
e 1, k 2;
i 3
i
e 2 e 2 i , k 3.
25.
Пример 4i
e 4 2 1 i , k 0;
2
i 3
2 k e 4 2 1 i , k 1;
i
4 1 e
2
4
3
i
2
4
1 i , k 2;
e
2
i
2
4
e
1 i , k 3.
2


















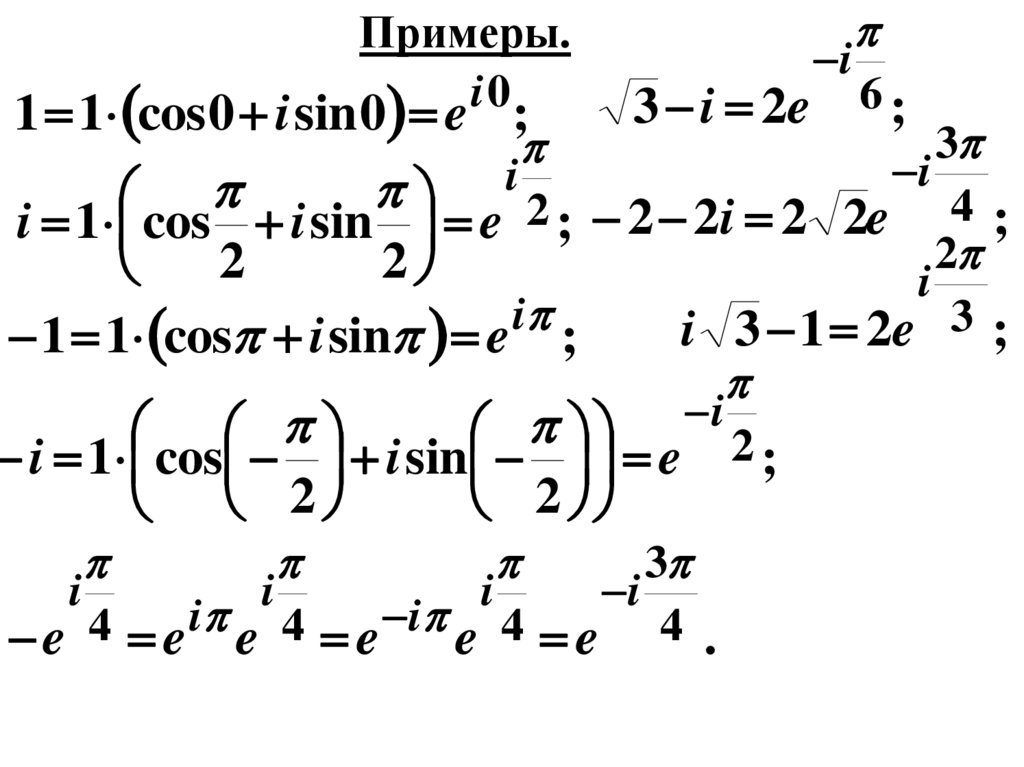


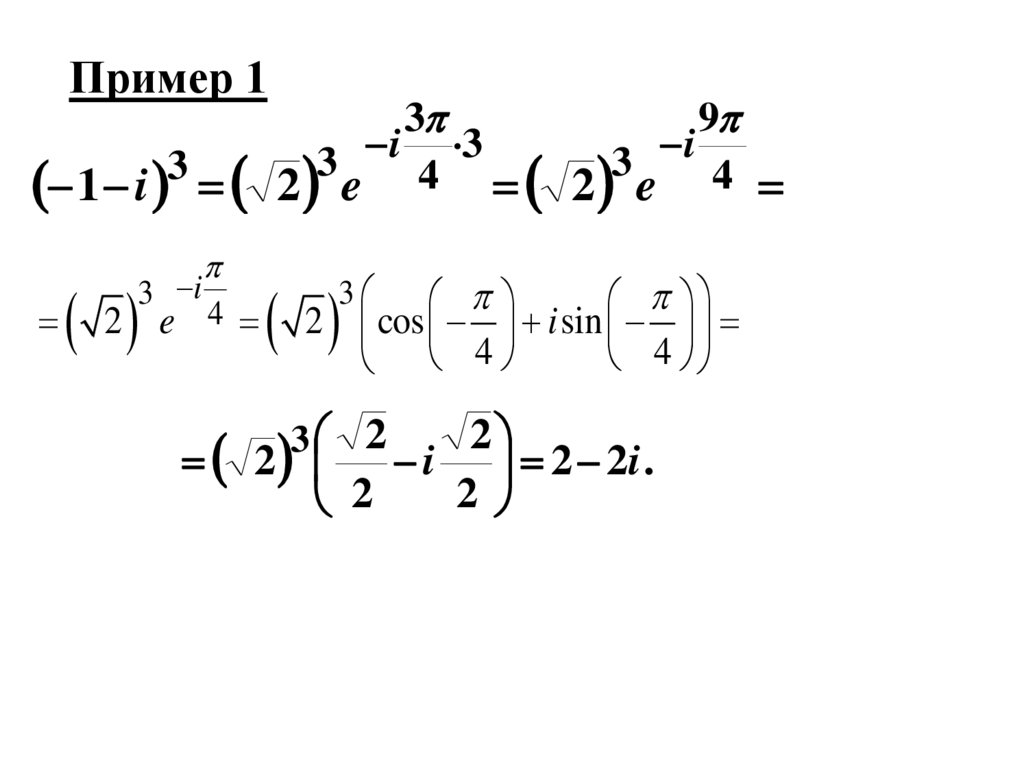



 mathematics
mathematics








