Similar presentations:
Свойства пространства-времени и интегралы состояния, четность
1.
Лекция 16СВОЙСТВА ПРОСТРАНСТВА-ВРЕМЕНИ
И ИНТЕГРАЛЫ СОСТОЯНИЯ: ЧЕТНОСТЬ
2.
→Предположим, что в пространстве имеется центр
симметрии. Это означает, что состояние системы,
состоящей из N частиц, не изменится при замене знака у
-r j
координат всех частиц, т.е. при замене r j
(j = 0, 1, …, N). Операция такого рода называется
инверсией, и можно ввести оператор инверсии ˆ :
ˆ f ( ) f ( ) .
Поскольку при наличии центра симметрии в пространстве
состояние системы не изменяется, гамильтониан системы
должен коммутировать с оператором инверсии:
ˆ H
ˆ ˆ .
ˆ H
(16.1)
Из (16.1) следует, что должен быть некоторый интеграл
состояния системы. В данном случае его называют
четностью состояния. Выясним, что это означает.
Предположим, что решение уравнения Шредингера для
стационарных состояний нам известно, в частности,
известна волновая функция Ψ(ξ). Поскольку операторы
и Hˆ коммутируют, у них должна быть общая система
собственных функций (см. окончание лекции 5).
ˆ
3.
Следовательно, волновая функция Ψ(ξ) будет собственнойфункцией и оператора инверсии ˆ :
ˆ =πΨ ,
πΨ
(16.2)
где π - собственное значение. Подействуем на это
уравнение оператором ˆ еще раз и учтем, что двукратное
действие этого оператора является тождественным
2
ˆ
=1 .
преобразованием, т.е.
ˆ = π ( πΨ)
ˆ
πˆ (πΨ)
πˆ 2Ψ = π πΨ
.
Ψ = π 2Ψ π 2 = 1 π = ±1
ˆ
ξ) ≡Ψ( -ξ
)= ±
Ψ( ξ
).
В итоге: πΨ(
Это означает: когда Ψ( -ξ) = +Ψ( ξ) , волновая функция
четная, а когда Ψ( -ξ) = -Ψ( ξ) - нечетная. Говорят, что
волновая функция обладает определенной четностью и это
ее свойство и будет интегралом состояния – четностью.
4.
Пример 1. Квантовая система – одномерный гармоническийосциллятор с массой m и частотой колебаний ω.
В этом случае гамильтониан имеет вид:
2
2
2
d
m
2
Hˆ
x
.
2m dx 2
2
Видно, что в точке 0 имеется центр симметрии, так как
Hˆ ( x ) Hˆ ( x ) ˆ Hˆ Hˆ ˆ . Следовательно, состояния такого
осциллятора должны обладать определенной четностью. И
действительно, можно показать, что решение уравнения
ˆ
x) = E Ψ( x) дает волновые функции Ψn(x),
Шредингера HΨ(
зависящие от квантового числа n = 0, 1, 2, …, и оно будет
определять четность состояний:
Ψn(-x) = (-1)n Ψn(x).
В итоге, состояния квантового осциллятора с четными
значениями n = 0, 2, … будут четными, а с нечетными
значениями n = 1, 3, … - нечетными.
5.
Пример 2. Квантовая система – частица, движущаяся вполе центральных сил.
В этом случае потенциальная энергия частицы зависит
только от r r x y z . Гамильтониан в этом случае
при замене r r изменяться не будет, и четность должна
быть интегралом состояния. Можно показать, что в данной
задаче в переменных (r, θ, φ) волновая функция имеет вид:
( r, , ) R( r )Ylm ( , ) ,
где вид функции R(r) зависит от вида потенциальной
энергии и находится из уравнения Шрёдингера, а Ylm ( , ) это уже известная нам сферическая функция с известными
свойствами. При операции инверсии r r в сферической
системе координат r r, , :
ˆ ( r ) ( r ) R( r )Ylm ( , )
( 1)l R( r )Y ( , ) ( 1)l ( r ) ( r ) .
2
2
lm
2
l
6.
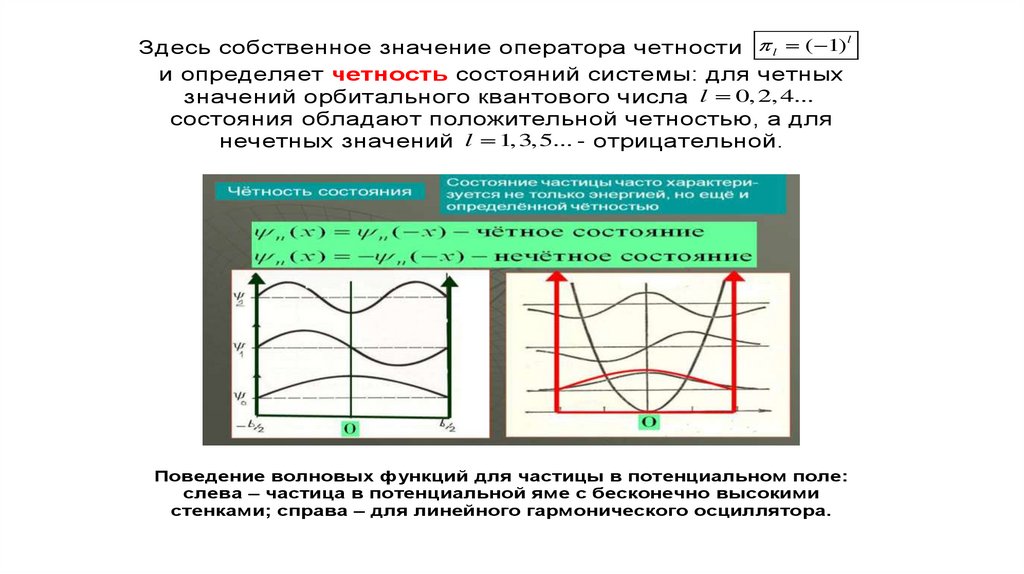
lЗдесь собственное значение оператора четности l ( 1)
и определяет четность состояний системы: для четных
значений орбитального квантового числа l 0, 2, 4...
состояния обладают положительной четностью, а для
нечетных значений l 1, 3, 5... - отрицательной.
Поведение волновых функций для частицы в потенциальном поле:
слева – частица в потенциальной яме с бесконечно высокими
стенками; справа – для линейного гармонического осциллятора.
7.
Предположим теперь, что имеется система частиц всиловом поле, имеющем центр симметрии, и частицы
взаимодействуют друг с другом. В этом случае
гамильтониан будет также включать слагаемое
1
2
N
N
Φ(ij
i =1 j =1( i ≠j)
rij ) , где Φ(ij
rij ) - потенциальная энергия
взаимодействия i-ой и j-ой частиц, rij ri - r j - расстояние
между ними (см. вид гамильтониана системы (9.9)).
Возникает вопрос: останется ли гамильтониан
симметричным и будет ли сохраняться четность? Для
разных типов взаимодействия (электромагнитного,
сильного и слабого) ответ был получен в 1956 г. физикамитеоретиками Т.Ли и Ч.Янгом совместно с физикомэкспериментатором Ц.Ву. Они проверили, что есть много
экспериментальных свидетельств относительно
электромагнитного и сильного взаимодействия: они
четность сохраняют. Однако для слабого
взаимодействия, из-за которого почти все наблюдаемые
элементарные частицы и многие атомные ядра
нестабильны и распадаются, таких доказательств
не было.
8.
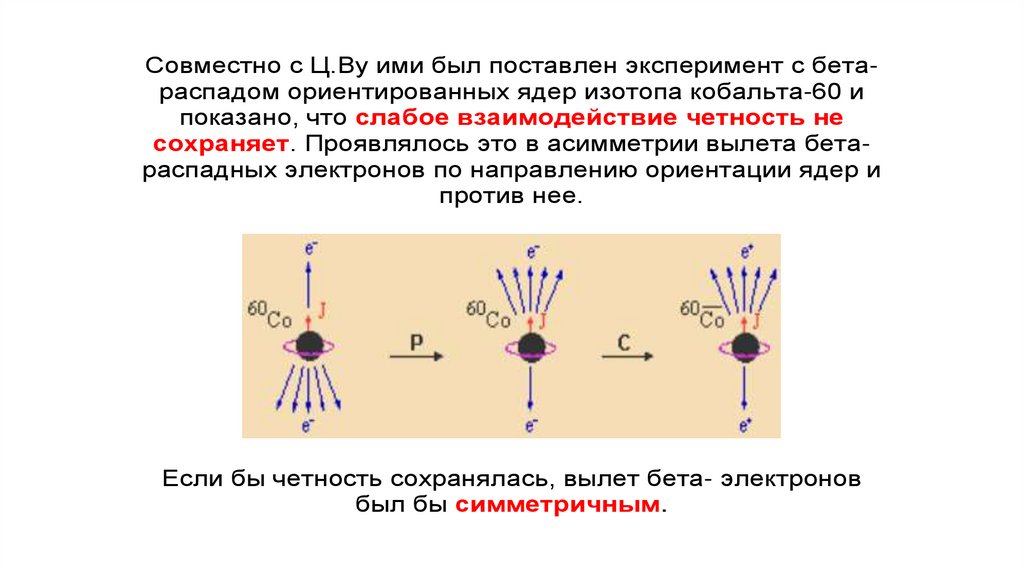
Совместно с Ц.Ву ими был поставлен эксперимент с бетараспадом ориентированных ядер изотопа кобальта-60 ипоказано, что слабое взаимодействие четность не
сохраняет. Проявлялось это в асимметрии вылета бетараспадных электронов по направлению ориентации ядер и
против нее.
Если бы четность сохранялась, вылет бета- электронов
был бы симметричным.
9.
За это открытие вышеперечисленные физики в 1957 годуполучили Нобелевскую премию по физике.
10.
Что является удивительным в этом открытии? Операцияинверсии с заменой r r - это замена декартовых
переменных x, y, z на -x, -y, -z, что эквивалентно замене
правой системы декартовых координат на левую (или
наоборот). Физики привыкли, что физические законы – это
объективная реальность, и они не зависят от того, в какой
системе координат (правой или левой) их описывать.
Результат должен был быть одинаков! Несохранение
четности же означает, что описание явления в правой или
левой системах координат даст различные результаты.
Для явлений с участием слабого взаимодействия это было
подтверждено экспериментально. Физика с такими
явлениями столкнулась впервые. Заметим, что в
классической физике такого интеграла состояния, как
четность, не существует, это квантовое понятие.
11. Проверочные вопросы к лекции 16. 1. Что означает интеграл состояния «четность»? 2. Какое свойство пространства способствует
сохранению четности состояния?3. Каковы собственные значения у оператора инверсии?
4. В чем суть опытов по проверки сохранения четности
при слабом взаимодействии?









 physics
physics








