Similar presentations:
Аналитические функции и конформные отображения
1.
Г лава 5А налитические ф ункции и
конф орм ны е отображ ения
2.
5 .1 А н а л и т и ч е с к и е ф у н к ц и иО п р ед елен и е 1 . Ф ун кц и я W f z
н азы вается
ан али ти ческой в т. z0, если он а ди ф ф ерен ц и руем а в каж дой
то ч к е н ек о то р о й о к р естн о сти т. z0.
3.
Зам ечание 1. И з определения следует, что ф ункция,ан ал и ти ч еская в т. z0 о б язательн о о каж ется ан али ти ч еско й
в каж д о й то чке н еко тор о й о кр естн о сти т. z0. П о это м у
м нож ество точек аналитичности ф ункции - откры тое
м нож ество.
4.
О п ред елен и е 2. Ф ун кц и я н азы вается ан али ти чн ой н ам н ож естве D , если она анали ти чн а в каж дой точке этого
м нож ества.
5.
П рим еры .1. Ф ун кц и я W z2 и м еет п рои звод н ую в каж д ой точке z C ,
следовательно она аналитична на всей ком плексной плоскости.
О пределение 3. Ф ункция, аналитичная на всей ком плексной
п лоскости , н азы вается ц елой .
6.
2. С ум м а f степ ен ного рядаa
n
z
z0
n
аналитична в
n 0
круге сходи м ости K
R
z z0 R .
Зам ечание 2. Д иф ф еренцируем ость ф ункции в точке и
ан али ти чн ость – разн ы е п он яти я. Е сли ф ун кц и я f
ан али ти чн а в н екоторой т. z0, то он а д и ф ф ерен ц и руем а в
этой точке. О братное м ож ет бы ть не верны м .
7.
П рим ер. Ф ункция w x3 3 x2yi определена на С .П роверим является ли она диф ф еренцируем ой.
Здесь U
x, y x 3, V x, y 3 x 2 y
U
V
V
2 U
3x ,
0,
6 xy,
3 x 2.
x
y
x
y
Ч астн ы е п рои звод н ы е н еп реры вн ы н а С . О д н ако услови я
Д Э К Р в ы п о л н и м ы е п р и 6 х у 0 , т е . п р и х 0 у 0 , т .е .
на осях координат. Н о в лю бой окрестности точки,
леж ащ ей на оси 0 х или 0 у найдется точка, в которой
ф ункция не является диф ф еренцируем ой. И так, данная
ф ункция диф ф еренцируем а на осях координат, но не
является аналитичной.
8.
Зам ечан и е 3. Н еред ко и сп ользуется п он яти е ан али ти ческойф ун кц и и в т. z .
О п р е д е л е н и е 4 .Ф у н к ц и я W f z , о п р е д е л е н н а я в н е к о т о р о й
окрестн ости т. z н азы вается ан али ти ческо й в т. z ,
1
е с л и ф у н к ц и я g f а н а л и т и ч н а в т . 0 .
9.
П рим ер1
f z оп ред елен а
z
1
ф у н к ц и ю g f
в о к р естн о сти т. z . Р ассм о тр и м
1
1 . Э та ф ун кц и я ан али ти чн а
1
в т . 0 . С л е д о в а т е л ь н о , f z = а н а л и т и ч н а в т . z .
z
10.
О тм етим некоторы е свойства аналитических ф ункций,вы текаю щ ие из определения аналитической ф ункции
и свойств диф ф еренцируем ы х ф ункций.
1 . Е с л и f1 и f 2 – а н а л и т и ч е с к и е ф у н к ц и и в о б л а с т и G ,
то и х сум м а, разн о сть, п р о и звед ен и е есть ф ун кц и и
f1
аналитические в области G . Ч астное
является
f2
ан ал и ти ч еск о й ф ун к ц и ей всю д у в G , гд е f2 0 .
11.
2 . М н о ж ест в о зн ач ен и й ф у н к ц и и w f z co n st,аналитической в области G плоскости
z
является областью
w .
3 . Е сл и w f z явл яется ан ал и ти ч еско й в о б л асти D
к о м п л е к с н о й п л о с к о с т и z , п р и ч е м в о б л а с т и е е з н а ч е н и й Е
к о м п л ек с н о й о б л а ст и w о п р ед е л ен а ан а л и ти ч е ск ая ф у н к ц и я
w , т о ф у н к ц и я f z я в л я е т с я а н а л и т и ч е с к о й
в плоскости
ф ункцией в области D .
12.
4 . Е сл и w f zпричем
f
/
z
является аналитической в области D ,
0, то в об ласти ее зн ачен и й Е оп ред елен а
о б р а т н а я ф у н к ц и я z w , я в л я ю щ а я с я а н а л и т и ч е с к о й
ф у н к ц и е й в Е . П р и э т о м , е с л и w 0 f z 0 , т о и м е е т м е с т о
равенство
/
w 0
1
f
/
z0
.
3ад ан и е. У м еть об осн овы вать лю б ое и з указан н ы х свой ств.
13.
5 .2 С о п р я ж е н н ы е г а р м о н и ч е с к и е ф у н к ц и иВ дальнейш ем м ы убедим ся, что ф ункция, аналитическая
в об ласти G , и м еет п рои звод н ую лю б ого п ор яд ка.
В частности для аналитической ф ункции f ее действительная
и м н и м ая части и м ею т н еп реры вн ы е частн ы е п рои звод н ы е
второго п оряд ка в об ласти G . К аж д ая и з п р ои звод н ы х
аналитической ф ункции является аналитической ф ункцией
и тем сам ы м непреры вной в G .
14.
uv v
u
П о л ьзуясь тем , ч то f z
i
i
, найдем f
x
x y
y
двум я способам и:
/
2
2
u
v
u
v
//
f z
i 2 i 2 ;
x x
x x x
x
u
v
2u
y i y y y 2
2u
2u 2v
2v
О тсю да
...?
,
...?
2
2
2
x
y
x
y 2
П оставьте вм есто точек необходим ы й
//
f z
y
2v
i 2
y
зн ак!
//
z
15.
2u 2u 2v 2v2u 2u
2v 2v
,
2 0,
2 0.
2
2
2
2
2
2
x
y
x
y
x
y
x
y
У равн ен и е такого ви д а н оси т н азван и е уравн ен и е Л ап ласа.
О пределение 1. Ф ункции, обладаю щ ие в некоторой области
н еп реры вн ы м и частн ы м и п рои звод н ы м и второго п оряд ка,
уд овлетворяю щ и м и уравн ен и ю Л ап ласа, н азы ваю тся
гарм они чески м и ф ун кц и ям и . К акое утверж ден и е м ож н о
сделать относительно действительной и м ним ой частей
а н а л и т и ч е с к о й ф у н к ц и и w f z ?
16.
Д ействительная и м ним ая части аналитической ф ункцииявляю тся гарм он и чески м и ф ун кц и ям и .
Е сл и ж е x, y и x, y – п р о и зво л ьн ы е гар м о н и ч ески е
ф у н к ц и и в о б л а с т и G , т о ф у н к ц и я F z x , y i x , y
н е о б язател ьн о б уд ет ан али ти ческой в G .
17.
О п ред елен и е 2. Д ве гарм он и чески е ф ун кц и и x, yи x , y ,
уд овлетворяю щ и е услови ям Д Э К Р а н азы ваю тся
соп ряж ен н ы м и гарм он и ческим и ф ункц и ям и.
И так, действительная и м ним ая части аналитической ф ункции
в области G являю тся соп ряж ен н ы м и гарм он и ческим и
ф ункциям и.
18.
П окаж ем , как п о од н ой и з соп ряж ен н ы х гар м он и чески хф ун кц и й м ож но н ай ти другую с точн остью д о п остоян ного
слагаем ого и тем сам ы м н ай ти ан али ти ческ ую ф ун кц и ю ,
если и звестн а ее д ей стви тельн ая и ли м н и м ая часть.
19.
П усть x, y– ф ун кц и я гарм он ическая в области G .
П окаж ем как найти аналитическую ф ункцию
f z u x , y iv x , y , д е й с т в и т е л ь н а я ч а с т ь к о т о р о й
u x , y x , y .
Д ля оты скания м ним ой части им еем два уравнения
u v
v u
Q x, y
P x , y .
x y
x
y
20.
uu
Ф ун кц и и P x, y
и Q x, y
непреры вны в G и
y
x
об лад аю т в G н еп реры вн ы м и частн ы м и п рои звод н ы м и
P
2 2 Q
2
.
2
y y y
y
x
x
В си лу чего?
21.
В с и л у у р а в н е н и я Л а п л а с а (га р м о н и ч е с к а я ф у н к ц и яу д о в л е т в о р я е т у р а в н е н и ю Л а п л а с а ).
x ,y
П оэтом у
P x , y d x
Q x , y d y н е за в и с и т о т п у т и
x0 ,y0
и н тегрирован и я, соеди н яю щ его т.
x0, y0 и
т. x, y
области G , следовательно представляет ф ункцию от
перем енны х x, y.
в
22.
x ,yП олож и м x, y
P x , y d x
Q x , y d y .
x0 ,y0
Т огд а x, y и м еет те ж е частн ы е п рои звод н ы е, что и
и с к о м а я ф у н к ц и я v x , y . Д е й с т в и т е л ь н о
v
P x, y .
x
x
v
Q x, y .
y
y
П о это м у v x, y
м о ж ет о тл и ч аться о т x, y
п остоян н ое слагаем ое c :
на
23.
x ,yx ,y
v х, у P d x Q d y
dx
dy С
x
x0 ,y0
x0 ,y0 y
В ы ч и сл яя v х, у
по этой ф орм уле, им еем две
д и ф ф е р е н ц и р у е м ы е ф у н к ц и и и u x , y x , y ,
v x , y x , y C , с в я з а н н ы е у с л о в и я м и Д Э К Р . О т с ю д а
с л е д у е т , ч т о f z u x , y i v x , y u x , y i x , y C
аналитическая ф ункция в D .
–
24.
Зам ечание. П о м ним ой части аналитической ф ункции м ож новосстановить ее действительную часть с точностью до
д ей стви тельн ого п остоян н ого слагаем ого.
25.
П рим ер. П усть область G получаетсяиз ком плексной области исклю чением
п о л у о с и .y 0 , x 0 . Л е г к о п р о в е р и т ь ,
что ф ун кц и я v x, y 2 e x co s y 2 x 3 y
гарм он и ческая в G . Д ей стви тельн о,
v
v
x
2e cos y 2;
2 e x s in y 3 ;
x
y
2
2v
v
x
x
2
e
c
o
s
y
;
2
e
cos y;
2
2
x
y
2v 2v
x
x
2
e
c
o
s
y
2
e
cos y 0;
2
2
x
y
26.
Ф у н к ц и я и ( х , у ) с о п р я ж е н н а я с v x , y , у д о в л е т в о р я е тусловиям Д Э К Р :
u v
u v
x
2 e s in y 3 ;
2ex cos y 2.
x y
y
x
27.
Т огдаx ,y
u x, y
x
x
2
e
s
i
n
y
3
d
x
2
e
c o s y 2 d y C
1 , 0
y
x
u x , y 3 d x
1
u x, y 3 x
x
1
2 e
x
c o s y 2 d y C
0
2 e x s in y
y
0
2 y
u x , y 3 x 2 e y s in y 2 y C
y
0
C
28.
5 .3 Г е о м е т р и ч е с к и й с м ы с л а р г у м е н т а им о д у л я п р о и зв о дн о й
П усть w f z
– аналитическая ф ункция в области G
ком плексной плоскости
и зоб раж ать в п лоскости
z . З н а ч е н и я ф у н к ц и и f б у д е м
w . К а ж д о й т . z x i y G б у д е м
с т а в и т ь в с о о т в е т с т в и е е д и н с т в е н н у ю т о ч к у w u iv в
плоскости
w .
29.
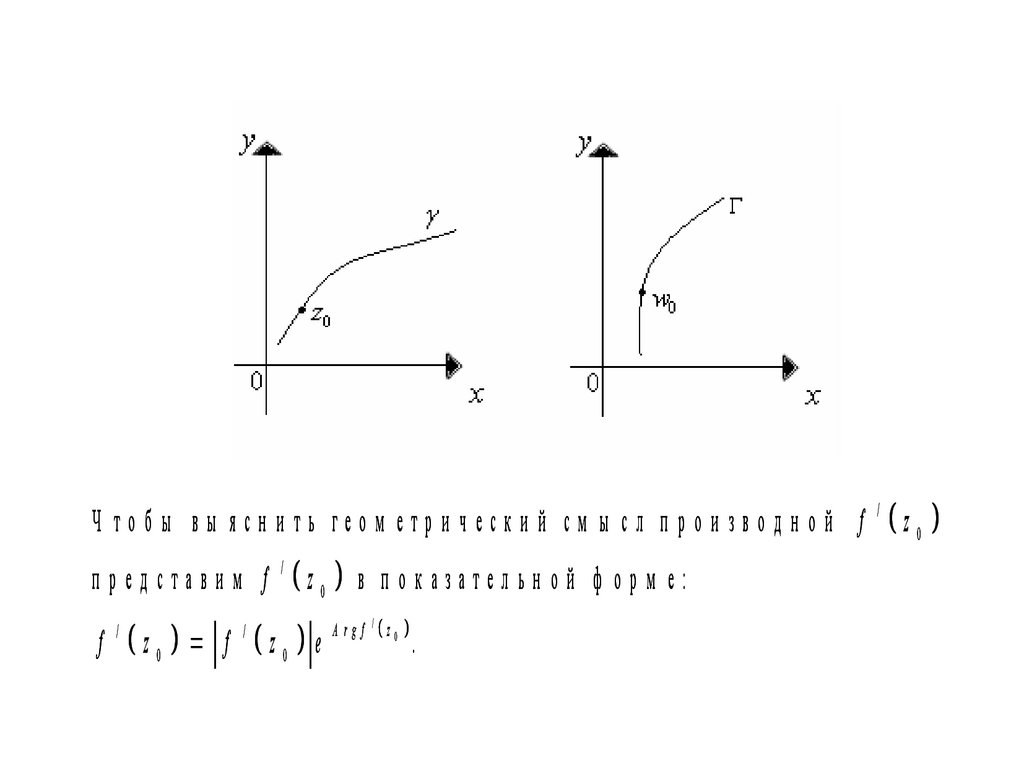
П усть z0 – п р о и зво л ьн ая то ч ка о б л асти G zи –
п р ох о д ящ ая ч ер ез т. z0 кр и вая, зад ан н ая со сво и м
н ап р авл ен и ем и и м ею щ ая о п р ед ел ен н ую к асател ьн ую в т. z0.
П редполож им , что f
/
z0 0.
В плоскости
будет кривая Г , проходящ ая через т. w
0
w о б р азо м
f z 0 .
кривой
30.
Ч то б ы вы ясн и ть гео м етр и ч ески й см ы сл п р о и зво д н о й fz0 в
/
z 0 e A rgf
представим f
f
/
z0
f
/
п о казател ьн о й ф о р м е:
/
z0
.
/
z0
31.
В озьм ем п р о и зво л ьн ую т. z0 z н а л и н и и и о б о зн ач и мо б р аз это й то ч к и f z0 z w 0 w . Э та то ч ка л еж и т н а
ли н и и Г . П ри стрем лен и и т. z0 z к z0 п о ли н и и
соответствую щ ая ей т. w 0 w движ ется п о линии Г к т. w 0,
причем z и w стрем ятся к нулю одноврем енно .
32.
И з равенстваw
i
f z 0 lim
k
e
находим
z 0
z
w
k , 2 lim A r g
z 0
z
/
w
1 l iz m 0
z
с т о ч н о с т ь ю д о к р а т н ы х 2 .
С ю да такж е входит требование: f
/
z0 0,
т .к . в п р о т и в н о м
случае н е и м ел б ы оп ред елен н ого зн ачен и я
33.
wР а с с м о т р и м р а в е н с т в о 2 . Т а к к а к A r g
A rg w A rg z,
z
т о р а в е н с т в о 2 п р и м е т в и д lim A r g w lim A r g z ( 3 ).
z 0
z 0
В ы ясн им геом етри чески й см ы сл равен ства
3 ,
очевидно
z z0 z z0 и зо б р аж ается векто р о м со ед и н яю щ и м т. z0
и z0 z. Т ак ж е w – есть вектор, соед и н яю щ и й точки w
и w 0 w .
0
34.
С лед овательн о A rg z есть угол м еж д у п олож и тельн ы мн ап равлен и ем О х и вектором z, а A rg w – угол Ф м еж д у
п олож и тельн ы м н ап равлен и ем оси О u и векторо м w . Т аки м
о б р а зо м , р а в е н с т в о (3 ) б у д е т и м е т ь в и д
Ч т о п р е д с т а в л я ю т с о б о й lim Ф и lim ?
z 0
z 0
lim Ф lim
z 0
z 0
4 .
35.
В пределе направлен ие вектора z совпадает с направлени емкасательн ой к ли н и и в т. z0, а н ап равлен и е w – с
н ап равлен и ем касательн ой к ли н и и в т. w 0, которая сущ ествует?!
О б озн ачая через и углы , об разован н ы е касательн ы м и к
ли н и ям и Г соответствен н о в точках z0 и w
0
с осям и О х и О u
п е р е п и ш е м ( 4 ) в в и д е : и л и . 5
36.
О пределение: Б удем считать полож ительны е направления осейО х и О u с о в п а д а ю щ и м и м е ж д у с о б о й . У го л - н а зы в а е т с я
углом п оворота касательн ой к кри вой в т. z0 п ри
отображ ении f .
Т аки м об разом , – уго л п ово рота касательн ой к ли н и и в т.
z0 п ри отоб раж ен и и f и ли и н аче – угол м еж д у
первоначальны м и отображ енны м направлениям и.
37.
П усть теп ерь чер ез т. z0 п роход и т ещ е ли н и я / и ее об разомп р и о т о б р а ж е н и и f я в л я е т с я Г /, п р о х о д я щ а я ч е р е з т . w 0.
6
П овторяя проведенны е рассуж дения, получаем
гд е
/
и / есть п р ед ельн ы е зн ач ен и я / и Ф
/
/ / ,
д л я л и н и й / и Г /.
38.
И з равенств7
5
и
6
/ / п о л уч и м
/ / и л и / / .
Зам ети в, что / и / – соответствен н о углы м еж д у
касательн ы м и к ли н и ям и / в т. z0 и Г и Г / в т. w 0,
усм атриваем из равенства
7
с л е д у ю щ е е :...? ...
39.
д ве п р о и зво л ьн ы е л и н и и , вы х о д ящ и е и з т. z0, о то б р аж аю тсяв д в е с о о т в е т с т в у ю щ и е л и н и и , в ы х о д я щ и е и з т . w 0 f z 0 ,
так что угол м еж ду касательн ы м и к данн ы м ли н иям и и х
об разам и б уд ет од и н и тот ж е как п о в ели чи н е, так и п о
направлению .
40.
Э т о о з н а ч а е т ,ч т о е с л и п о л о ж и т е л ь н о е н а п р а в л е н и е л и н и и вт. z0 п ереход и т в п олож и тельн ое н ап равлен и е ли н и и / п утем
п оворота н а н екоторы й уголв оп ределен н ом н аправлен и и , то
соответствую щ ее направление линии Г переходит в направление
Г / п утем п оворота н а тот ж е угол и в том ж е н ап равлен и и .
41.
И так, отображ ение с пом ощ ью аналитической ф ункции обладаетс в о й с т в о м с о х р а н е н и я (к о н с е р в а т и зм а ) у гл о в в т е х т о ч к а х , гд е
п рои звод н ая f
/
z 0.
42.
В ы ясн и м теп ерь геом етри чески й см ы сл м од уля п рои звод н ой .w
Р а в е н с т в о 1 м о ж е т б ы т ь п е р е п и с а н о т а к l i m
k 8 .
z 0 z
Г е о м е т р и ч е с к и z о з н а ч а е т д л и н у в е к т о р а z , т .е . р а с с т о я н и е
м еж ду точкам и z0 и z0 z ан алоги чн о w – расстоян и е м еж д у
то ч кам и w 0 и w 0 w . Ч то п о казы вает р авен ство
8 ?
43.
Равенство8
п о казы вает, ч то о тн о ш ен и е б еско н еч н о м ал о го
расстояния м еж ду отображ енны м и точкам и к бесконечно
м алом у расстоянию м еж ду первоначальны м и точкам и, равное
в пределе k f
/
z0
н е зав и си т о т н ап р а в л ен и я л и н и и .
44.
И з этого ясно, что k f/
z0
м ож но рассм атривать как
вели чи н у м асш таб а в т. z0 п ри отоб раж ен и и п осред ством
ф у н к ц и и w f z .
Е с л и k 1 р а с с т о я н и е у в е л и ч и в а е т с я , т .е . п р о и с х о д и т
р а с т я ж е н и е ; е с л и k 1 ,т о н а о б о р о т п р о и с х о д и т с ж а т и е п р и k 1
р а с с т о я н и е о с т а е т с я н е и з м е н н ы м , т .е . б е с к о н е ч н о м а л ы й
элем ен т, вы ход ящ и й и з т. z0, зам ен яется эк ви вален тн ы м ем у
б е с к о н е ч н о -м а л ы м э л е м е н т о м , в ы х о д я щ и м и з т . w 0.
45.
И так, м од уль п рои звод н ойf
/
z0 м о ж
но рассм атри вать как
коэф ф ициент растяж ения в т. z0 при отображ ении посредством
ф у н к ц и и w f z .
46.
П р и м е р . Ф у н к ц и я w 1 i2 z и м е е т п р о и з в о д н у ю w / 2 i иявляется аналитической во всей плоскости
п лоскости . М од уль п рои звод н ой w
/
/
z
,
w
0 во всей
2i 2. О тображ ение
п р о и зво д и т р астяж ен и е в каж д о й то ч ке п л о ско сти с
коэф ф ициентом 2.
a rg w a rg 2 i . С л е д о в а т е л ь н о в к а ж д о й т о ч к е п р о и с х о д и т
2
вращ ен и е н а угол
.
2
/
47.
5 .4 . К о н ф о р м н ы е о т о б р а ж е н и яО п ределен и е 1. О тоб раж ен и е, которое в т. z0 сохран яет углы и
об лад ает п остоян ством растяж ен и й , н азы вается кон ф орм н ы м в
т. z0.
О п ред елен и е 2. О тоб раж ен и е н азы вается ко н ф орм н ы м в
области, если оно конф орм но в каж дой точке области.
48.
З а м е ч а н и е . И з п о л у ч е н н ы х р е з у л ь т а т о в в п у н к т е 5 .3 . в ы т е к а е т ,что отображ ение, осущ ествляем ое с пом ощ ью аналитической
ф ун кц и и w f z
в точке z0, гд е f
/
z0 0
обладает свойствам и
сохран ен и я углов и п остоян ством растяж ен и й , следовательн о
оно является конф орм ны м .
49.
П рим еры .1 i
1) w 2 z 4 z 1 к о н ф о р м н о в т. z 0
.
2
2 ) w 1 i2 z к о н ф о р м н о н а в с е й п л о с к о с т и .
2
50.
К ак б ы л о д о казан о , сво й ство со х р ан ен и я угло в о зн ач ает, ч тосохран яется н е только абсолю тн ая вели чи н а углов м еж ду
кри вы м и , п ересекаю щ и м и ся в т. z0, н о и и х н ап равлен и я.
51.
О пределение 3. О тображ ения, при которы х сохраняю тсяаб солю тн ы е вели чи н ы углов м еж д у кри вы м и и и х об разам и ,
н о нап равлени я углов м ен яю тся н а п ротиво полож ны е,
н а зы в а ю т с я к о н ф о р м н ы м и о т о б р а ж е н и я м и II р о д а .
Р ассм отрен н ы е ран ее отоб раж ен и я, н азы ваю тся отоб раж ен и ям и
I рода.
52.
П р и м ер . П усть д ан о о то б р аж ен и е w z.Б уд ем и зоб раж ать п ерем ен н ую w
в то й ж е п л о ско сти , ч то и z. В и д и м ,
что при рассм атриваем ом
отображ ении всякая т. z переходит
в т. z, сим м етричную т. z
относительно действительной оси.
Я сно, что при таком отображ ении
всякие два направления, вы ходящ ие
и з т. z и об разую щ и е м еж д у соб ой
угол п ерей дут в два соответствую щ их
направления, сим м етричны е с первы м и,
угол м еж ду которы м и .
53.
Т аки м об разом , вели чи н а углов сохран яется, н ап равлен и еотсчета м еняется как обратное. Д алее это отображ ение
о б л а д а е т с в о й с т в о м п о с т о я н с т в а р а с т я ж е н и й , т .к . п р и н е м н е
п р ои сх о д и т и зм ен ен и е м асш таб а
z
z . С ледовательно,
рассм атриваем ое отображ ение есть конф орм ное отображ ение
II р о д а .
54.
Е сли w f z – ан али ти ческая в об ласти G и в этой об ластиf
/
z 0,
I рода.
то отображ ение, осущ ествляем ое ею есть конф орм ное
55.
П ред п олож и м , что w f zобласти f
/
z 0 .
аналитична в области G , и в этой
П окаж ем , что отоб раж ен и е f z явл яется
к о н ф о р м н ы м II р о д а .
В сам ом деле, это отображ ение м ож ет бы ть рассм отрено как
ко м п ози ц и я д вух о тоб раж ен и й w f z
и w.
56.
П ри п ервом углы сохран яю тся как п о вели ч и не, так и п он ап равлен и ю , п ри втором н ап равлен и е отсч ета углов м ен яется
н а п роти воп олож н ое. К ром е того, дан н ое о тоб раж ен и е
о б л а д а е т с в о й с т в о м п о с т о я н с т в а р а с т я ж е н и й , т .к . э т о с в о й с т в о
присущ е обоим составляю щ им отображ ениям .
57.
И так, всякое отображ ение, устанавливаем ое при пом ощ иф ун кц и и , зн ачен и я которой являю тся соп ряж ен н ы м и со
зн ачен и ям и ан али ти ческой ф ун кц и и , есть к он ф орм н ое
о т о б р а ж е н и е 2 -г о р о д а .
О б р а т н о , п у с т ь к о н ф о р м н о е о т о б р а ж е н и е II р о д а о с у щ е с т в л я е т с я
при пом ощ и ф ункции w F
z .
Т о гд а F z
является
к о м п л е к с н о с о п р я ж е н н о й а н а л и т и ч е с к о й ф у н к ц и и F z .
Д о казать сам о стоятел ьн о .
58.
5 .5 О д н о л и с т н ы е ф у н к ц и и . О б л а с т иодн оли стн ости ан али ти ческ ой ф унк ц и и .
О п ред ел ен и е. Ф ун кц и я w f z
н азы вается о д н о л и стн о й в
об ласти G , если в разли чн ы х точках этой о б ласти он а п ри н и м ает
разли чн ы е зн ачен и я.
59.
Зам ечан и е. И з этого оп ределен и я следует, что всякаяоднолистная ф ункция им еет обратную .
П рим еры .
1 ) w a z b о д н о л и с т н а н а в с е й п л о с к о с т и С . П у с т ь z1 z 2
w 2 w 1 a z 2 b a z1 b a z 2 z1 0 , т .е . w 1 w 2 .
60.
12) w о п р ед ел ен а н а D C 0 и о д н о л и стн а.
z
1
1
z1 z 2
П у с т ь z1 z 2 , w 2 w 1
0 , т .е . w 1 w 2 .
z 2 z1 z1 z 2
61.
3) w e z, область определения D С .Е с л и z 1 x1 iy1, z 2 x 2 iy 2 , т о e
z1
= e x1 , e
z2
= e x2 .
П о л о ж и м т е п е р ь x1 x2 x и y1 y 2.
Т огда e
z1
e
z2
e
x
e
y1
e
y2
e
x
c o s y
1
i s in y 1 c o s y 2 i s in y 2
y1 y 2
y1 y 2
y1 y 2
y1 y 2
e 2 s in
s in
2icos
s in
2
2
2
2
x
y y2
i 1
y
y
y
y
y
y
y
y
x
2
1
2
1
2
1
2
2
2 ie x s in 1
c
o
s
i
s
i
n
2
i
e
s
i
n
e
.
2
2
2
2
62.
Э то вы раж ен и е об ращ ается в н уль только в тех точках, гд еy1 y 2
s in
0 ,т .е . п р и y 1 y 2 2 K , K Z .
2
И так, эта ф ункция не является однолистной, однако для нее
м о ж н о указать так н азы ваем ую о б ласть о д н о л и стн ости , те. такую
об ласть, в разли чн ы х точках которой ф ун к ц и я п ри н и м ает
разли чн ы е зн ачен и я.
63.
М ы п оказали , ч то ez1
e
z2
т о гд а и т о л ь к о т о гд а , к о гд а x1 x 2,
y1 y 2 2 K , K Z . П о это м у, есл и в ы б ер ем о б л асть в в и д е
полосы ш ириной 2 со сторонам и параллельны м и
д е й с т в и т е л ь н о й о с и , т о в н у т р и н е е в д в у х р а зл и ч н ы х т о ч к а х z1 z 2
ф ун кц и я w e z б уд ет п ри н и м ать р азли ч н ы е зн ачен и я.
64.
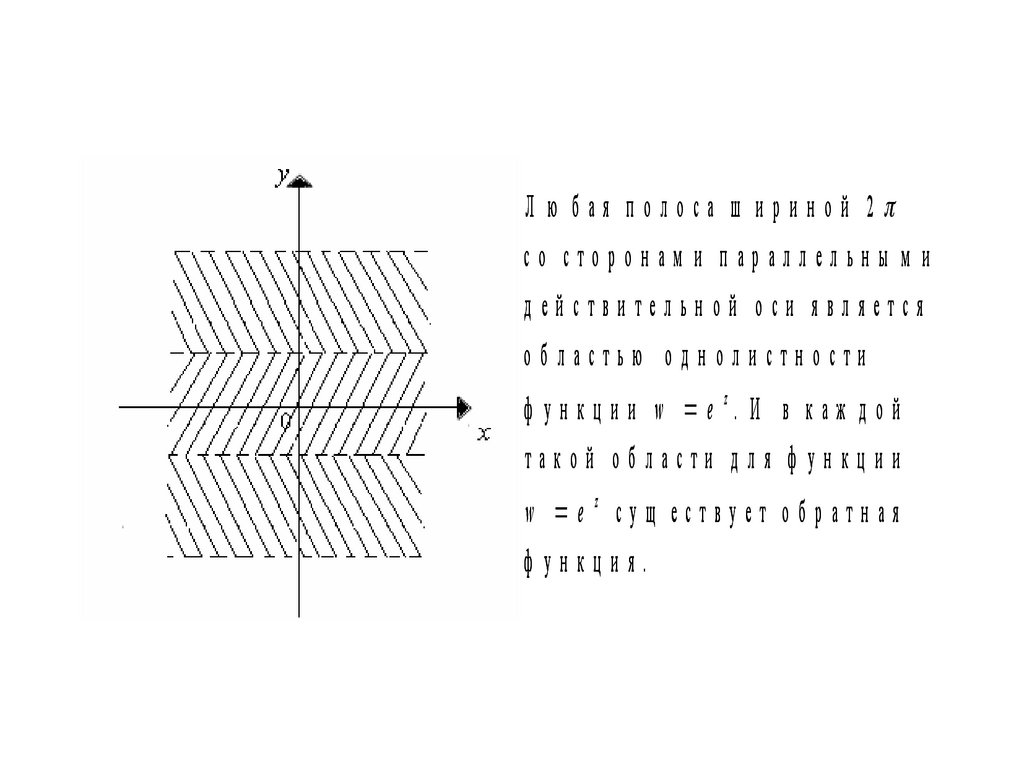
В заш тр и х о ван н о й о б л асти w e z о д н ол и стн а.65.
Л ю бая полоса ш ириной 2со сторонам и параллельны м и
действительной оси является
областью однолистности
ф ун к ц и и w e z. И в к аж д о й
такой области для ф ункции
w ez сущ ествует обратная
ф ункция.
66.
Задание. Д окаж ите, что ф ункция w zn не являетсяоднолистной и покаж ите, что область однолистности для нее
2
есть угол с верш и н ой в н ачале коорд и н ат раствором
.
n






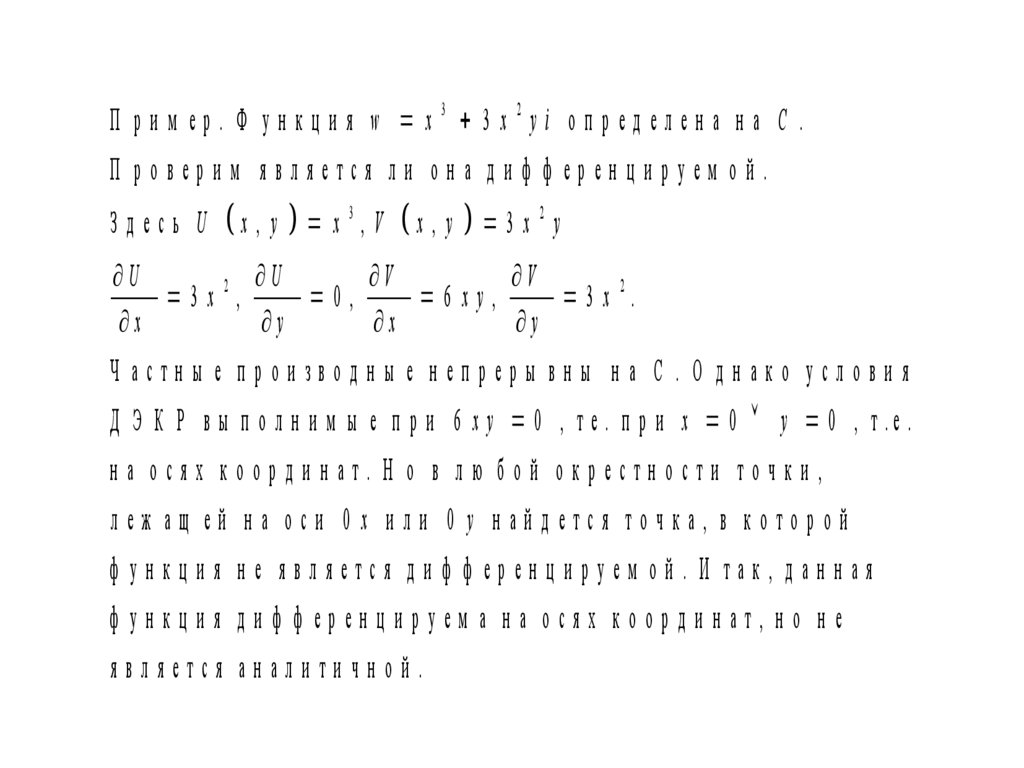
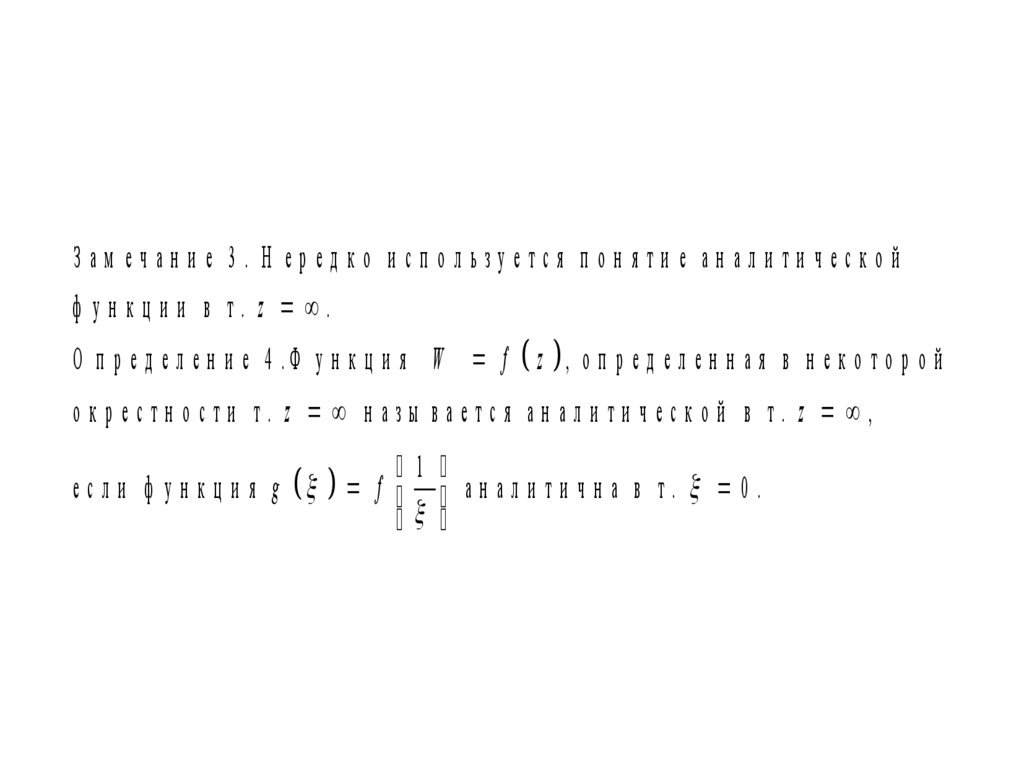
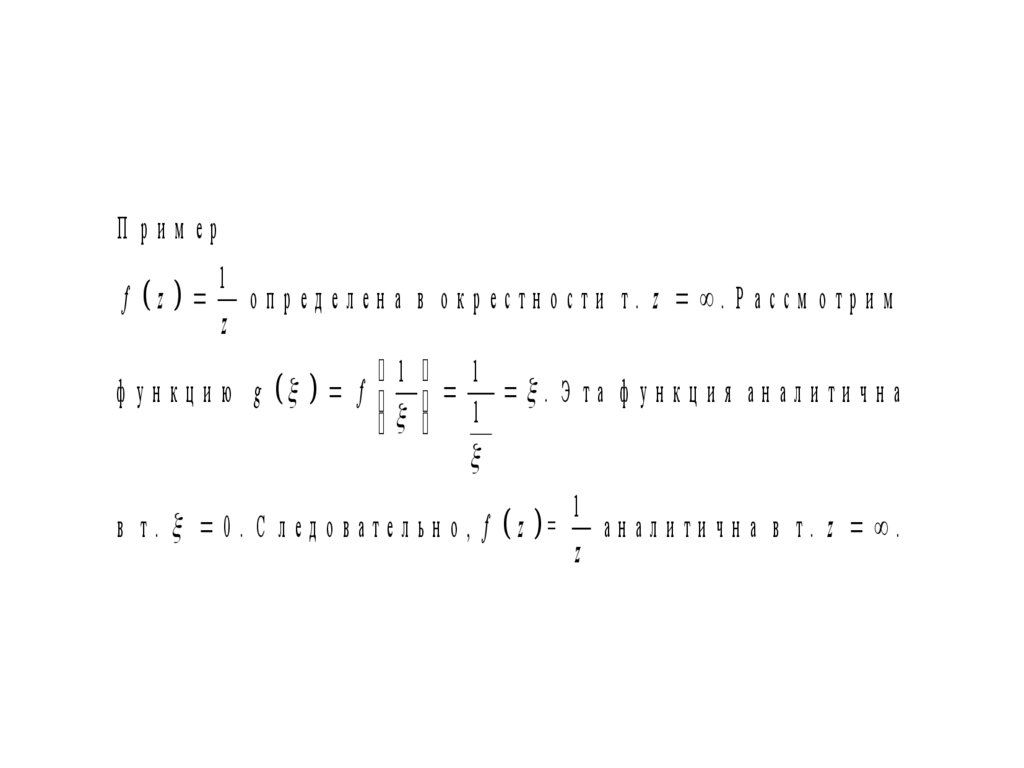


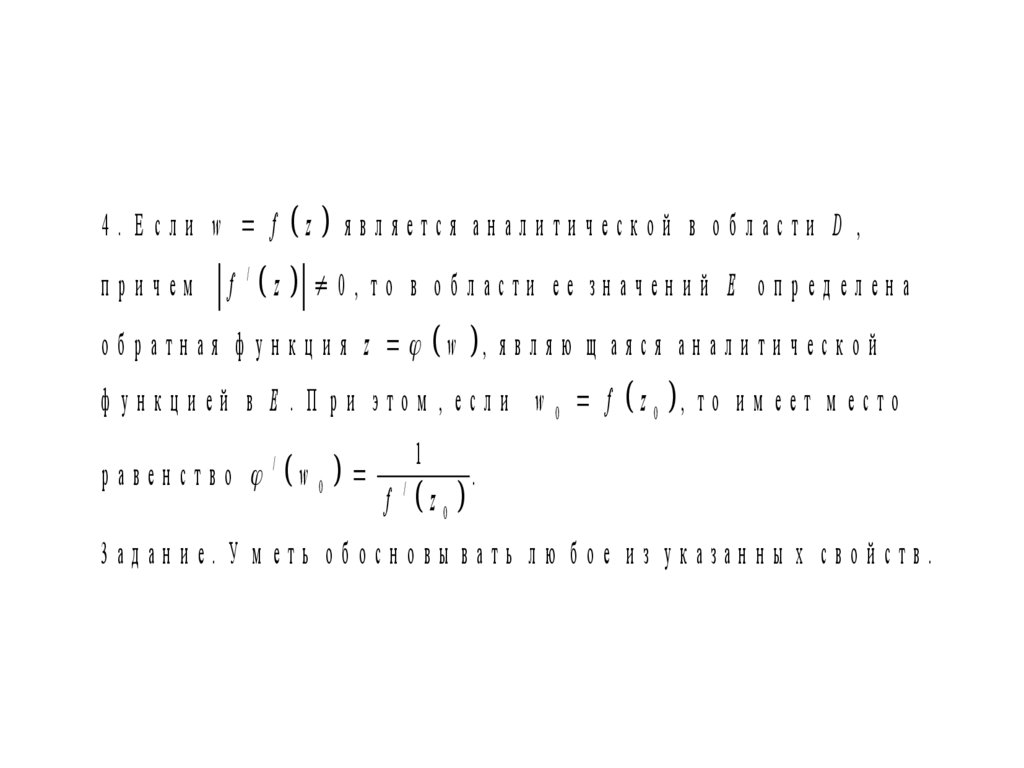






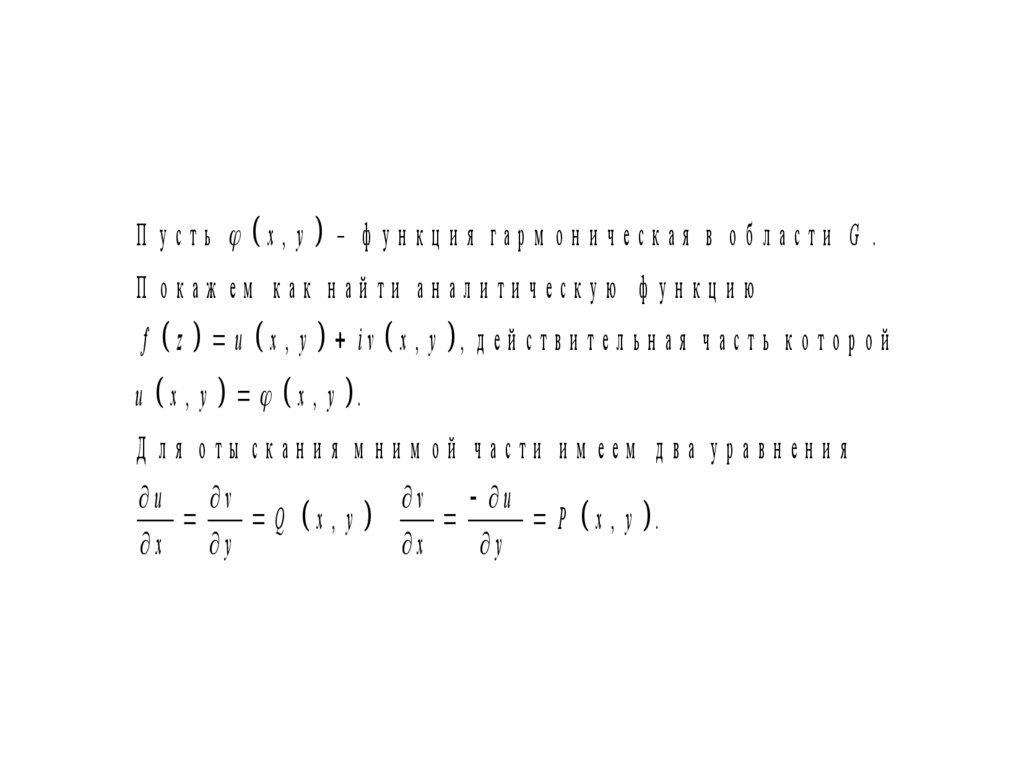
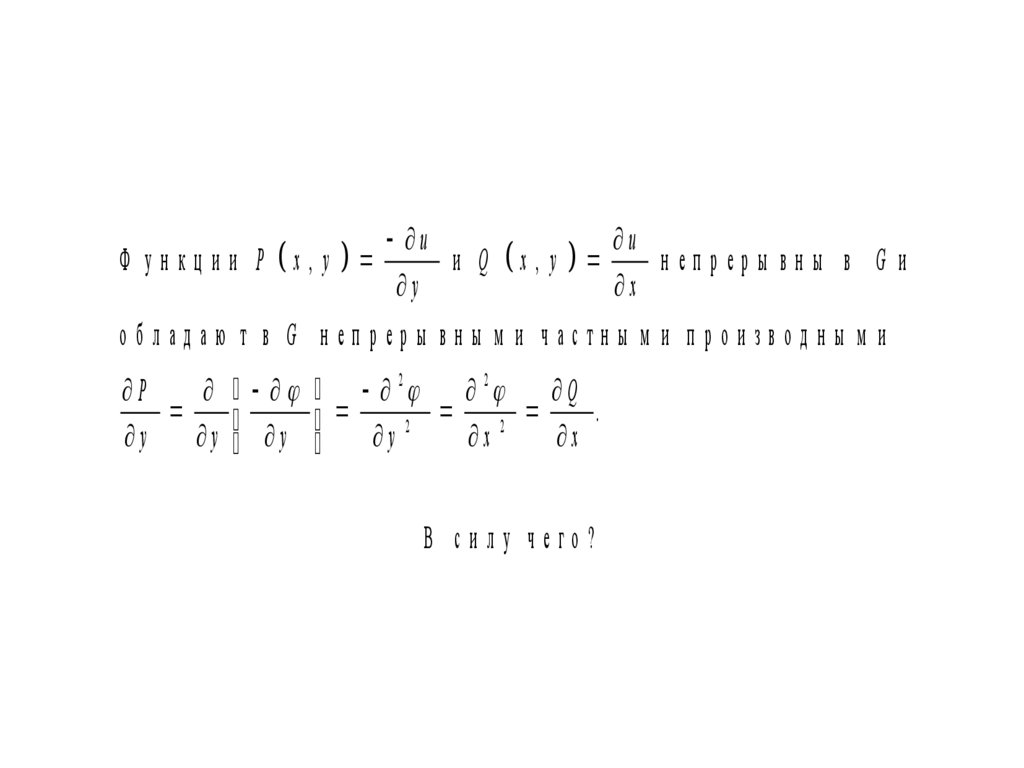

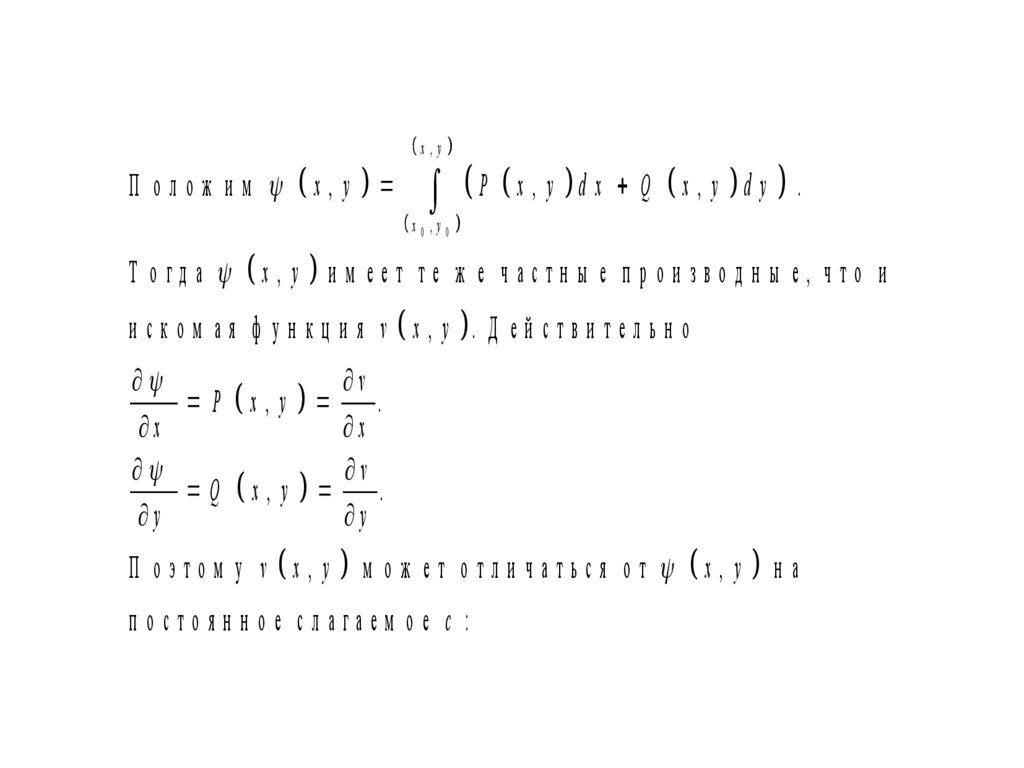
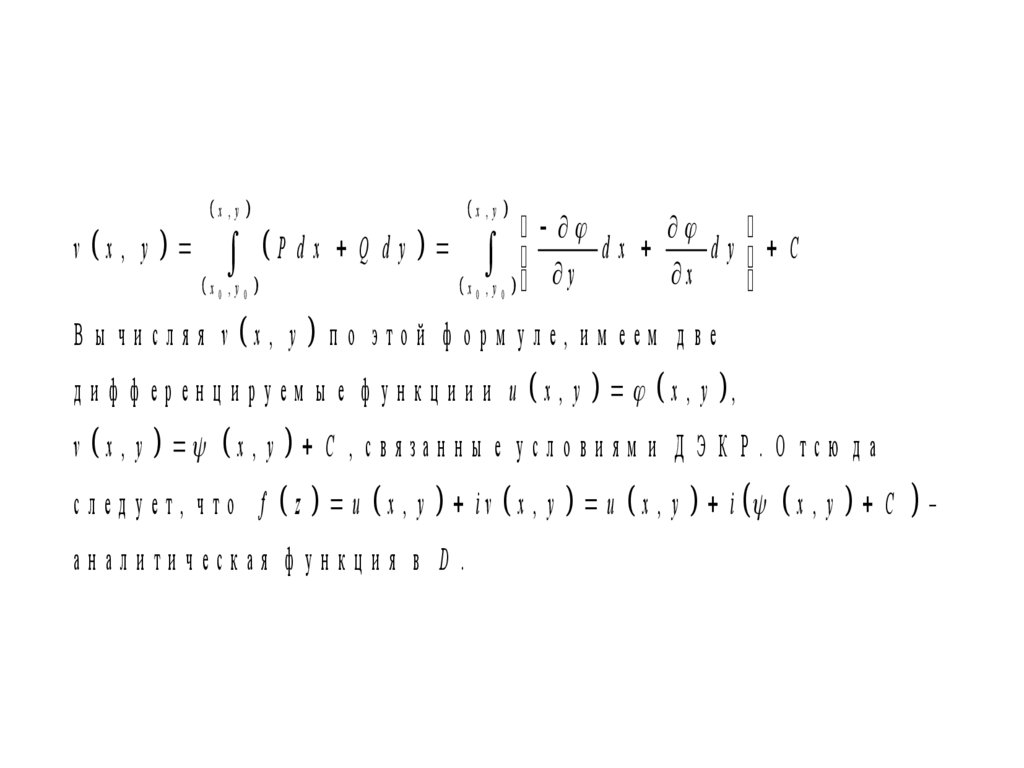







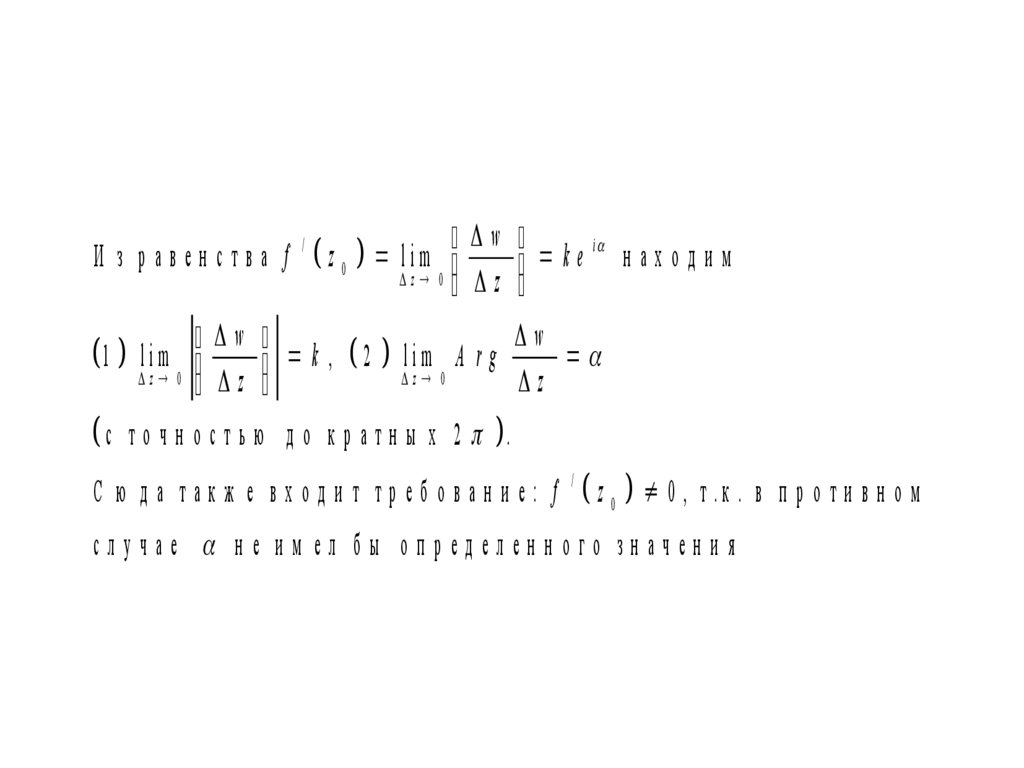



























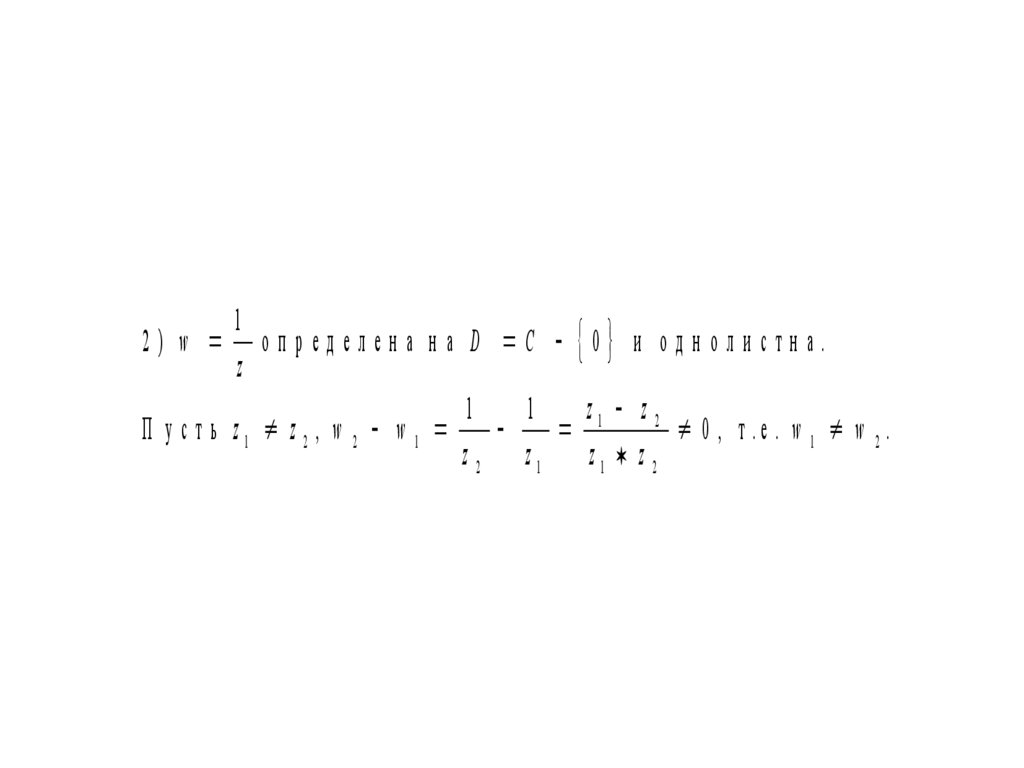






 mathematics
mathematics








