Степени вершин графа. (Лекция 15)

1. Степени вершин графа

2.

Определение 1
Степенью (валентностью) вершины называется число инцидентных ей ребер.
Обозначают: o(V ), deg(V ) .
Определение 2
Вершина степени 1 называется висячей.
Вершина степени 0 называется изолированной.
Пример
2
.7
1
5 – висячая вершина.
7 – изолированная вершина.
3
4
6
5

3.

Определение 3
Граф называется однородным (регулярным), если степени
k
R
всех его вершин равны. Обозначают: n , где k – степень каждой вершины
графа, n – число вершин графа.
Число, которому равны степени всех вершин,
называется степенью данного однородного графа.
Пример
7
1
2
4
8
1
6
2
5
3
3 4
R42
R83

4.

Теорема 5
Сумма степеней всех вершин графа есть четное число,
равное удвоенному количеству ребер.
Теорема 6
Число вершин нечетной степени в любом графе четно.
Теорема 7
В любом графе обязательно найдутся две вершины,
имеющие одинаковую степень.
Теорема 8
В любом однородном графе либо его порядок,
либо его степень – четное число.
Определение 9
Последовательность степеней всех вершин графа
называется степенной последовательностью графа.

5.

Пример
1
G
2
6
3
4
5
(1, 3, 2, 4, 1, 1) или (13, 2, 3, 4) - степенная последовательность графа G.

6.

Пример
По степенной последовательности
(12 ,22 ,32 )
можно построить графы

7. Задача 1

Доказать, что если в графе с n вершинами (n>2)
ровно две вершины имеют одинаковую степень,
то в этом графе либо в точности одна вершина степени 0,
либо в точности одна вершина степени (n-1).
Решение. Допустим противное.
1) В графе ровно две вершины одинаковой степени, и это
вершины степени 0. Тогда, удалив из графа эти изолированные
вершины, получим граф, степени всех вершин которого
различны, что невозможно по теореме 3.
2) Если же в графе ровно две вершины одинаковой степени, и
это вершины степени (n-1), то перейдя к дополнению , получим
противоречие, аналогично пункту 1).

8. Задача 2

Существуют ли графы с данной степенной последовательностью? Ответ
пояснить.
1) (1;2;3;4);
2) (13;22;3;5);
3) (0;1;2;3;42);
4) (12;23;32;4);
5) (12;32;4).
Решение.
1) Не существует, так как все степени различные (смотри теорему 7).
2) Не существует, так как число вершин нечетной степени нечетно, а именно 5
( смотри теорему 6).
3) Не существует(смотри задачу 1).
4) Построим граф, имеющий данную степенную последовательность
5) Не существует, так как, соединив вершину степени 4 с четырьмя из
оставшихся вершин, убеждаемся, что для вершин степени 3 не достаточно
смежных вершин.

9. Задача 3

• а) Опишите n вершинный однородный
граф степени 2.
• б) Опишите n вершинный однородный
граф степени n-1.
• Решение.
• а) Многоугольник с n вершинами.
• б) Полный n вершинный граф.

10.

Подграфы.
Операции над графами

11.

Определение 1
Граф порядкаn называе тся помеченным,
если его вершинам присвоены неко торые метки,
n .
например, номера 1,2,…,
Пример
3
1
2
3
1
4
G1
4
3
4
2
G2
2
1
G3
G1 G2 , G1 G3 , где G1 , G2 , G3 помеченные графы.
G1 G2 G3 , где G1 , G2 , G3 непомеченные (абстрактные) графы.

12.

Определение 2
Пусть дан граф G (V , E ) . Граф G1 (V1 , E1 ) называется подграфом
(частью графа G), если V1 V , E1 E .
Если при этом V1 V , то такой подграф называется остовным.
Определение 3
Пусть дан граф G (V , E ) . Подграф G1 (V1 , E1 ) графа G называется порожденным,
если для любых вершин u, v V (u, v) E (u, v) E .
1
1
Определение 4
(V1 , E1 ) и G2 (V2 , E2 ) называют граф
G (V , E ) G1 G2 такой, ч то V V1 V2 , E E1 E2 .
Объединение графовG1 иG2 называется дизъюнктным, если V1 V2 .
Обозначают: G G1 G2 .
Объединением графов G1

13.

Пример
1
1
Граф G
2
Порожденный по дграф графа G
6
7
2
6
3
5
3
5
4
Остовный по дграф графа G
По дграф графа G, не являющийся
ни остовным, ни порожденнным
1
2
2
6
. 6
7
. 7
3 .
. 5
4
5

14.

Примеры
5
1
2
3
4
1
2
4
3
G1
1
3
5
1
2 2
4
3
G1 G2
G2
4
1
4
5
3
2 5
2
G1
G2
G1 G2

15.

Определение 5
(u, v) - ребро графа G (V , E ) .
G
Граф G( u ,v ) G (u , v) получается из графа
Пусть
т. е.
в результате у даления ребра
(u, v)
V (G( u ,v ) ) V (G ), E (G( u ,v ) ) E (G ) \ (u, v) .
Пример
u
G
v
u
v
G(u,v)
,

16.

Определение 6
G
Пусть v - вершина графаG . Граф G( v ) G v получается из графа
v и всех инцидентных ей ребер,
в результате удаления вершины
т.е. V (G( v ) ) V (G ) \ v , E (G( v ) ) E (G ) \ (v, u ) | u V (G ) .
Пример
u
G
G(u )

17.

Определение 7
Пусть u и v - две вершины графа G
(V , E ) .
x
Удалим э ти вершины из графаG и добавим новую вершину
,
соединив ее ребром с каждой вершиной, вхо дящей в объединение
G .
окружений вершинu иv в исхо дном графе
u v
G отождествлением вершин
Построенный граф получился из графа
u
Отождествление вершин
если
vи
(u, v) E (G ) .
и
.
называется стягиванием ребра(u, v)
,
Пример
1
2
x
3
4
2
3
5
6
4
6
G
G'
x
2
5
4
6
G"

18.

Определение 8
G' , если
G' получаетсяGиз
Граф G называется стягиваемым к графу
в результате неко торой последовательности стягивания его ребер.
Пример
G
G1
Граф G (носящий название графа Петерсена) стягивается к графу
G1
=K5.

19.

Определение 9
Пусть v - вершина графаG
. Рассмотрим два множества N 1 (v) иN 2 (v) ,
объединение которых совпадает с о кружениемN (v)
Удалив вершинуv , добавим новые вершиныv1 ,v2
Соединим v1 с каждой вершиной из N 1 (v) , vа2
вершины v .
и ребро(v1 , v2 ) .
- с каждой вершиной изN 2 (v)
v
Произведенная операция называется расщеплением вершины
*
а полученный граф обозначаетсяGv
.
,
.

20.

Пример
a
b
c
b1
b2
a
d
f
c
d
f
g
g
G
h
h
G
*
b
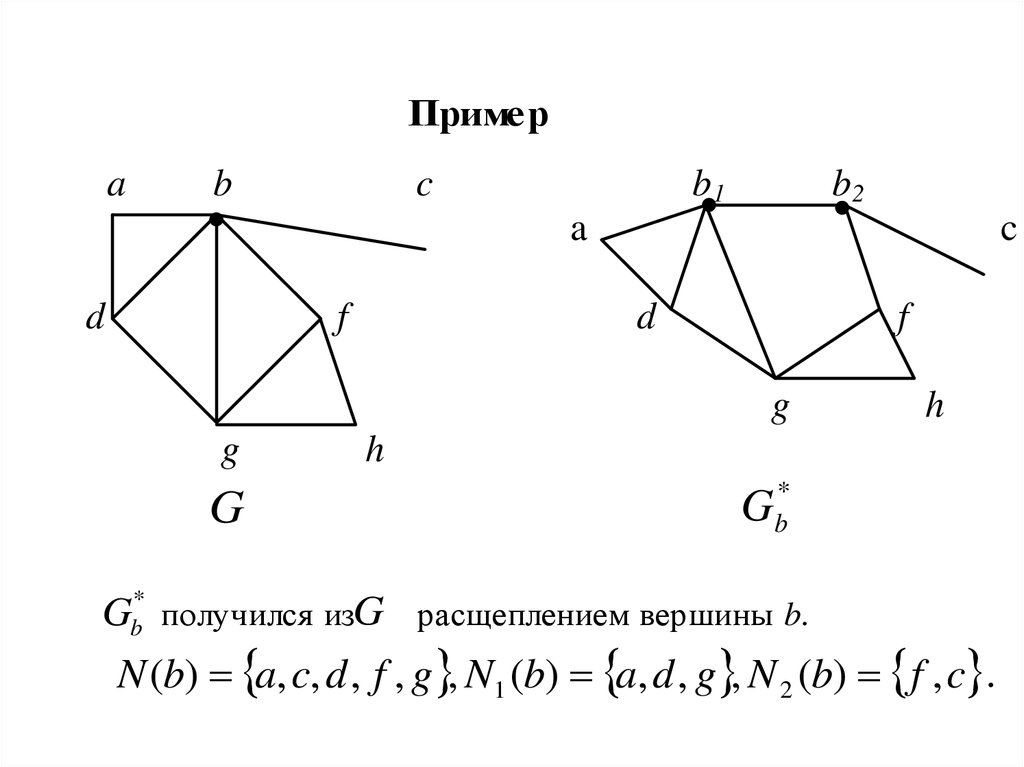
Gb* получился изG расщеплением вершины b.
N (b) a, c, d , f , g , N1 (b) a, d , g , N 2 (b) f , c .

21.

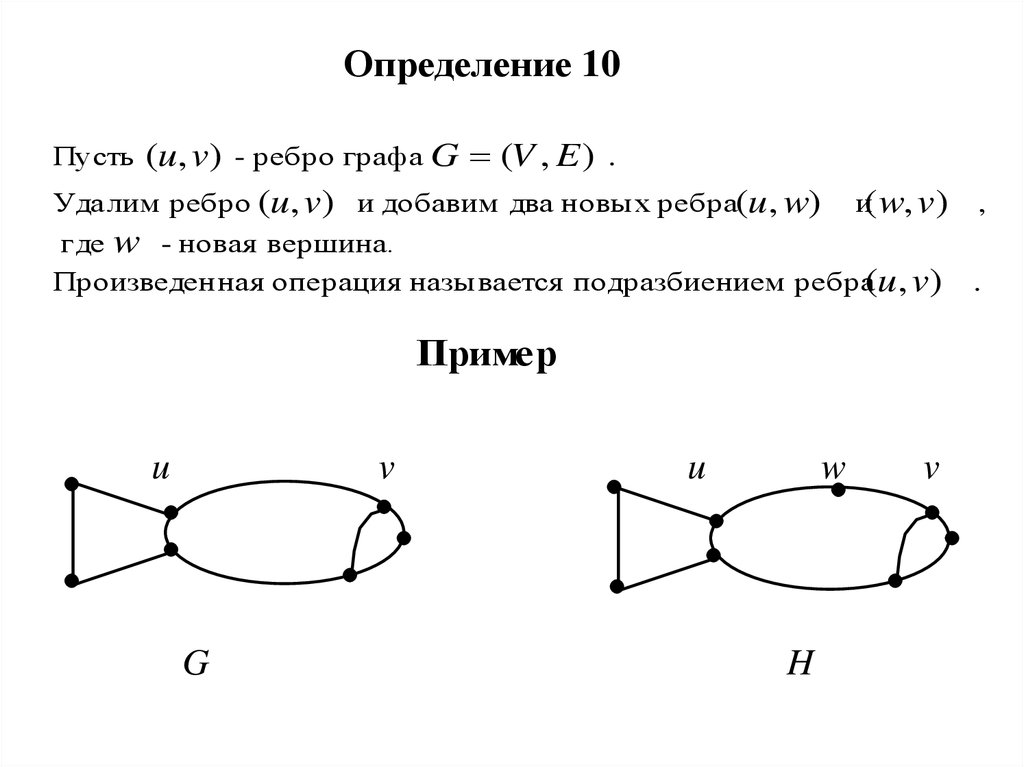
Определение 10
(u, v) - ребро графа G (V , E ) .
Уда лим ребро (u, v) и добавим два новых ребра(u, w)
где w - новая вершина.
Пусть
и( w, v)
,
Произведенная операция называется подразбиением ребра(u, v)
.
Пример
u
v
G
u
w
H
v

22.

Определение 11
1.
Декартовым произведением G1 G2 называется граф G,
для которого V(G)= V1 xV2 - декар тово произведение множеств вершин
исхо дных графов, а E(G) определяется следующим образом: вершины
(и 1, u 2 ) и (v1 , v2 ) смежны в графе G тогда и только то гда,
когда или и 1=v1 , а u 2 и v2 смежны в G2 , или и 2=v2 , а u 1 и v1 смежны в G1 .
2. Категорийным произведением G1xG2 называется граф G,
для которого V(G)= V1xV2 - декартово произведение
множеств вершин исходных графов, а E(G) определяется следующим образом:
вершины (и1, u2) и (v1, v2) смежны в графе G тогда и только тогда,
когда u1 и v1 смежны в G1 и u2 и v2 смежны в G2.
3. Сильным произведением G1 x G2 называется граф G,
для которого V(G)= V1xV2 - декартово произведение
множеств вершин исходных графов, а E(G) определяется следующим образом:
вершины (и1, u2) и (v1, v2) смежны в графе G тогда и только тогда,
когда u1, v1 смежны в G1, а u2, v2 смежны в G2 или и2=v2,
или u2, v2 смежны в G2, а u1, v1 смежны в G1 или и1=v1.

23.

Пример