Similar presentations:
Последовательности. Способы задания числовых последовательностей
1.
ПОСЛЕДОВАТЕЛЬНОСТИРаботу выполнял:
Сташков
Кирилл
Ученик 9 Г класса
Школы №116
2.
ПоследовательностьПоследовательность-это упорядоченный список элементов
некоторого множества
Функцию y=f(х), называют функцией натурального аргумента или
числовой последовательностью, обозначают как y=f(n) или y1, y2, y3 … yn .
Для yn, n – индекс, он задает порядковый номер элемента
последовательности.
Если в последовательности встречаются многоточия, то так принято
обозначать последующие члены. Для последовательности y1, y2, y3 … yn,
имеется ввиду что после y3 идут y4, y5, y6 и так далее. Возле члена yn
подразумевается запись yn−1, yn, yn+1.
Последовательности можно обозначать любыми буквами латинского
алфавита.
Способы задания числовых последовательностей:
1. Аналитический способ
2. Словесный способ
3. Рекуррентный способ
4. Графический способ
3.
1.Аналитический способ.Аналитический способ - Последовательность задается формулой n-го члена: an=f (n).
По этой формуле можно найти любой член последовательности.
Пример1:Известно выражение k-го члена числовой последовательности: ak = 3+2·(k+1).
Вычислите первые четыре члена этой последовательности.
Решение.
a1=3+2∙(1+1)=3+4=7;
a2=3+2∙(2+1)=3+6=9;
a3=3+2∙(3+1)=3+8=11;
a4=3+2∙(4+1)=3+10=13.
Пример2: yn=C.
Наша последовательность всегда принимает значение равное С, то есть имеет вид:
С,С,С,С… Такую последовательность называют стационарной.
Зная формулу n-ого члена последовательности, нетрудно найти любой член
последовательности. А вот если задана последовательность, но неизвестна формула для
n-ого члена, чаще всего удается задать последовательность в аналитическом виде.
4.
Пример3: Дана последовательность 1,3,5,7,9…Очевидно, что перед нами последовательность нечетных чисел. Тогда аналитическая
форма будет в таком виде: yn=2n−1.
Пример4: Дана последовательность 5,15,20,25…
Номер члена последовательности умножается на пять, тогда в аналитическом виде
имеем: yn=5n.
Пример5: 8,13,18,23…
Каждый член последовательности на 5 больше предыдущего. 8=5+3, тогда получаем,
что наша последовательность задана в виде: yn=5n−3.
2. Словесный способ.
Чаще всего такой способ применяют, когда нет возможности задать
последовательность аналитически (или это очень сложно) или
последовательность состоит из небольшого количества членов.
Пример1: 1,3,5,6,9,10,15.
Нашу последовательность задать в аналитической форме не
представляется возможным, тогда просто произносят члены
последовательности.
5.
3.Рекуррентный способ.Последовательность также задается формулой, но не формулой общего
члена, зависящей только от номера члена. Задается формула, по которой
каждый следующий член находят через предыдущие члены. В случае
рекуррентного способа задания функции всегда дополнительно задается
один или несколько первых членов последовательности.
Данный способ позволяет вычислять члены последовательности, через
предыдущие ее члены.
Используя данный способ, мы как бы всегда возвращаемся назад, вычисляя
предыдущие члены. Почти всегда задана формула, позволяющая вычислять n
член через предыдущие члены.
Выписать первые четыре члена последовательности {an},
если a1=7; an+1 = 5+an.
Решение.
a2 =5+a1=5+7=12 ;
a3 =5+a2=5+12=17;
a4=5+a3=5+17=22.
Ответ: 7; 12; 17; 22; ... .
6.
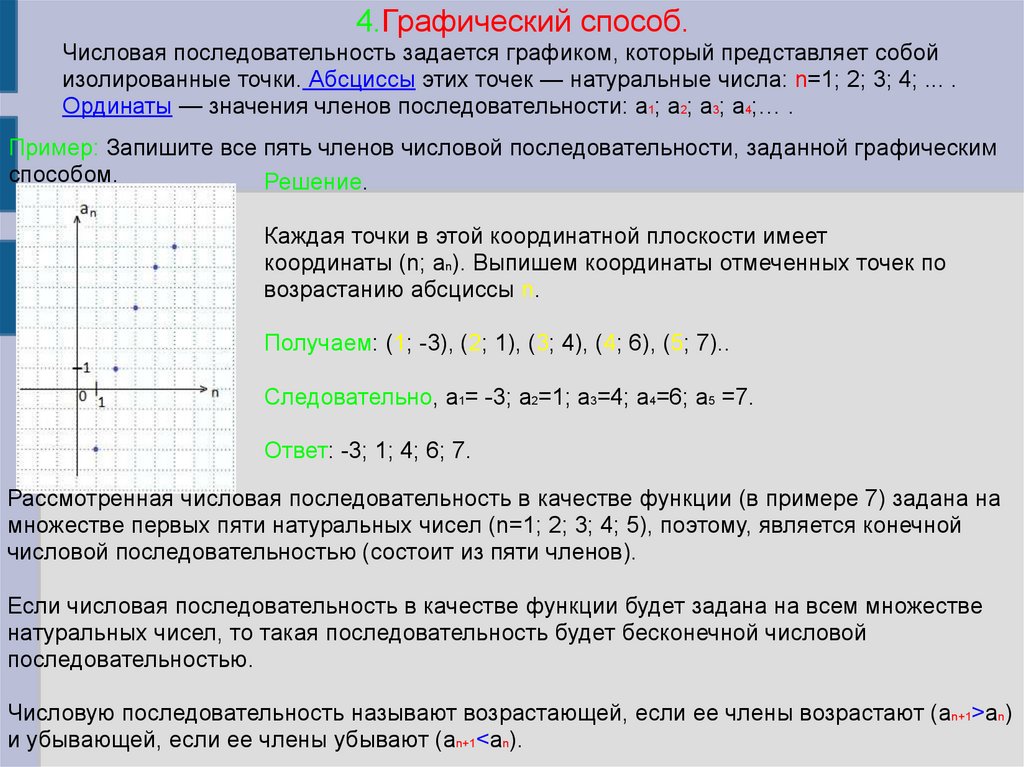
4.Графический способ.Числовая последовательность задается графиком, который представляет собой
изолированные точки. Абсциссы этих точек — натуральные числа: n=1; 2; 3; 4; ... .
Ординаты — значения членов последовательности: a1; a2; a3; a4;… .
Пример: Запишите все пять членов числовой последовательности, заданной графическим
способом.
Решение.
Каждая точки в этой координатной плоскости имеет
координаты (n; an). Выпишем координаты отмеченных точек по
возрастанию абсциссы n.
Получаем: (1; -3), (2; 1), (3; 4), (4; 6), (5; 7)..
Следовательно, a1= -3; a2=1; a3=4; a4=6; a5 =7.
Ответ: -3; 1; 4; 6; 7.
Рассмотренная числовая последовательность в качестве функции (в примере 7) задана на
множестве первых пяти натуральных чисел (n=1; 2; 3; 4; 5), поэтому, является конечной
числовой последовательностью (состоит из пяти членов).
Если числовая последовательность в качестве функции будет задана на всем множестве
натуральных чисел, то такая последовательность будет бесконечной числовой
последовательностью.
Числовую последовательность называют возрастающей, если ее члены возрастают (an+1>an)
и убывающей, если ее члены убывают (an+1<an).
7.
Монотонные последовательности.Последовательность называется возрастающей, если каждый следующий член больше
предыдущего.
Последовательность называется убывающей, если каждый следующий член меньше
предыдущего.
Убывающие и возрастающие последовательности называют монотонными
последовательностями.
Пример. 1,3,5,7,9…. – возрастающая последовательность.
Пример. 1,-1,-3,-5… – убывающая последовательность.
Пример. 1,-1,3,-3,5,-5… – ни возрастающая, ни убывающая последовательность.
n
Пример. yn=2 . Члены нашей последовательности: 2,4,8,16…. Последовательность
возрастает.
n
yn=a , если а>1, то последовательность возрастает, если 0<а<1, то последовательность
убывает.






 mathematics
mathematics








