Similar presentations:
В мире графов
1.
В мире графов2.
Математические теории и методы буквальнопронзили все другие науки, в том числе и
гуманитарные. Если раньше развитие математики
происходило под влиянием запросов физики и
техники, то в современном обществе математика
помогает организовать производство, планировать
экономику, управлять промышленностью,
государством, общественными процессами. Теперь
математический аппарат используется не только
как инструмент расчетов, но и способствует
решению задач выбора наиболее эффективного
варианта в реальных жизненных проблемах.
Одним из методов решения таких задач является
метод математического моделирования, одним из
его инструментов является теория графов.
3.
• Впервые основы теории графовпоявились в работах Леонарда Эйлера.
Он применил графы для решения
задачи нахождения оптимального пути.
Эйлер решил обозначать пункты
точками, а путь - отрезками,
соединяющими эти точки.
Совокупность этих фигур и назвали
графом.
4.
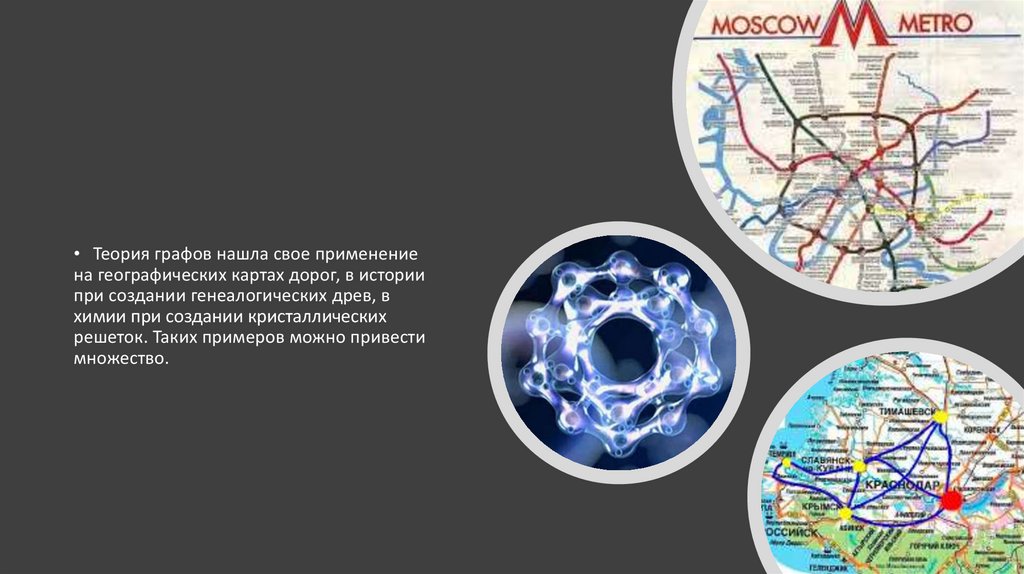
• Теория графов нашла свое применениена географических картах дорог, в истории
при создании генеалогических древ, в
химии при создании кристаллических
решеток. Таких примеров можно привести
множество.
5.
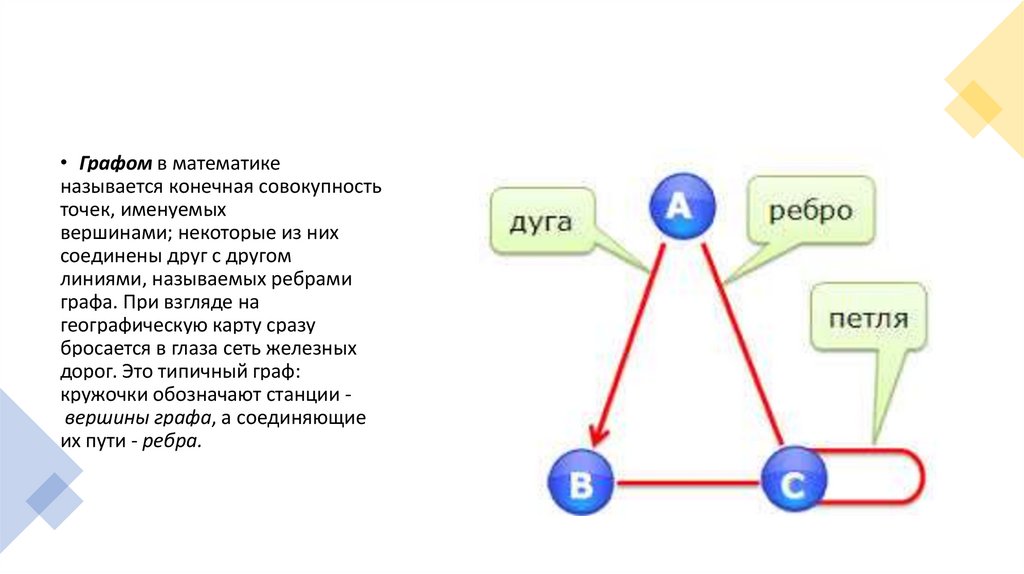
• Графом в математикеназывается конечная совокупность
точек, именуемых
вершинами; некоторые из них
соединены друг с другом
линиями, называемых ребрами
графа. При взгляде на
географическую карту сразу
бросается в глаза сеть железных
дорог. Это типичный граф:
кружочки обозначают станции вершины графа, а соединяющие
их пути - ребра.
6.
• Родоначальником теории графов принято считатьматематика Леонарда Эйлера (1707-1783, российский
математик, швейцарец по происхождению, академик
Петербургской и Берлинской академии наук).
• Он предложил изящное решение знаменитой задачи
о семи Кенигсбергских мостах в 1736 году, а также
придумал общий метод решения подобных задач.
• Семь мостов Кёнигсберга существовали в
Кёнигсберге (нынешнем Калининграде) в XVI XX веках.
Издавна среди жителей Кёнигсберга была
распространена такая загадка: как пройти по всем
мостам, не проходя ни по одному из них дважды?
Многие кёнигсбержцы пытались решить эту задачу как
теоретически, так и практически, во время прогулок. Но
никому это не удавалось, однако не удавалось и
доказать, что это даже теоретически невозможно.
7.
На упрощённой схеме части города (графе) мостам соответствуют линии(рёбра графа), а частям города — точки соединения линий (вершины
графа). В ходе рассуждений Эйлер пришёл к следующим выводам:
1. Число нечётных вершин (вершин, к которым ведёт нечётное число
рёбер) графа всегда четно.
2. Невозможно начертить граф, который имел бы нечётное число
нечётных вершин.
3. Если все вершины графа чётные, то можно, не отрывая карандаша от
бумаги, начертить граф. При этом можно начинать с любой вершины
графа и завершить его в той же вершине.
4. Граф с более чем двумя нечётными вершинами невозможно начертить
одним росчерком.
8.
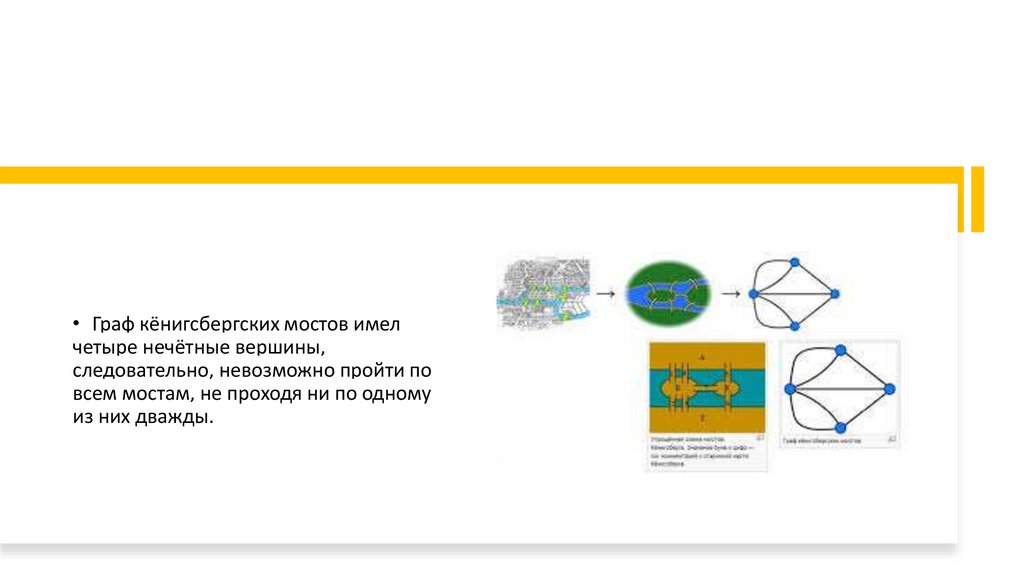
• Граф кёнигсбергских мостов имелчетыре нечётные вершины,
следовательно, невозможно пройти по
всем мостам, не проходя ни по одному
из них дважды.
9.
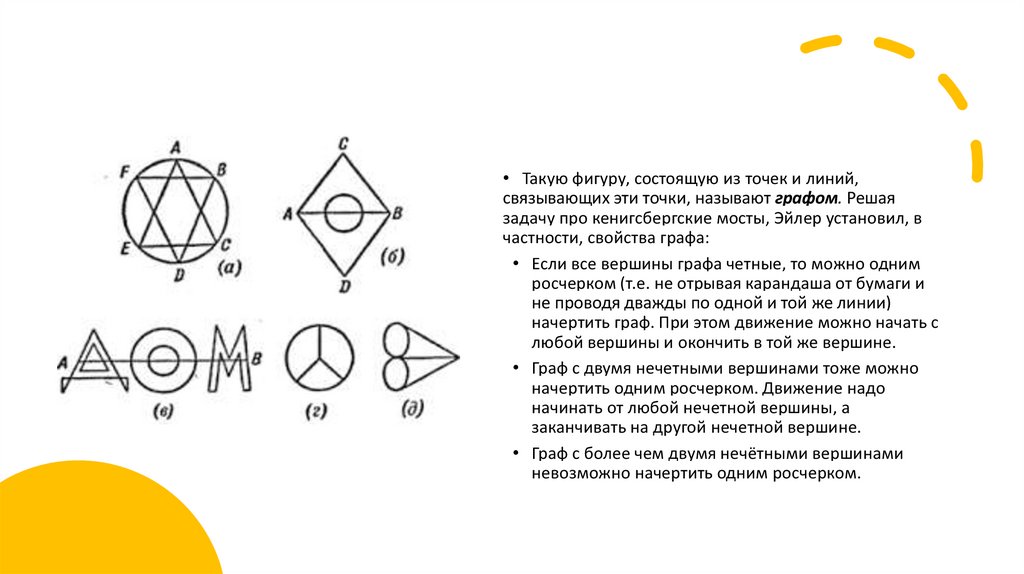
• Такую фигуру, состоящую из точек и линий,связывающих эти точки, называют графом. Решая
задачу про кенигсбергские мосты, Эйлер установил, в
частности, свойства графа:
• Если все вершины графа четные, то можно одним
росчерком (т.е. не отрывая карандаша от бумаги и
не проводя дважды по одной и той же линии)
начертить граф. При этом движение можно начать с
любой вершины и окончить в той же вершине.
• Граф с двумя нечетными вершинами тоже можно
начертить одним росчерком. Движение надо
начинать от любой нечетной вершины, а
заканчивать на другой нечетной вершине.
• Граф с более чем двумя нечётными вершинами
невозможно начертить одним росчерком.
10.
• Теория графов зародилась при решении головоломок изанимательных задач, в настоящее время она стала простым,
доступным и удобным средством решения широкого круга
важных практических задач. Особенно велико значение этого
метода как универсального языка при создании
математических моделей. Благодаря доступности и
наглядности, графы могут успешно использоваться в
обучении математике в школе, при решении практических
жизненных задач. Изучение основ теории графов позволяет
развивать мышление обучающихся, направленное на
восприятие изучаемых объектов, моделирование реальных
ситуаций или проблем. Использование теории графов
вызывает интерес в силу своей простоты и понятности, это
позволяет развивать навыки абстрактного и логического
мышления, творческий подход к решению задач, помогает
свободнее пользоваться различными языковыми средствами
математики.





 mathematics
mathematics








