Similar presentations:
ТВП Лекция 1 2 3 17 марта последняя
1.
Теория вычислительных процессов и структурЦелебровская Марина Юрьевна
[email protected]
Ссылка на курс в DiSpace:
https://dispace.edu.nstu.ru/didesk/course/show/6910/1
2.
Теория вычислительных процессов и структурЛекции – 18 часов
Практические работы – 4 работы
Расчетно-графическая работа
В конце семестра – зачет
3.
Формирование рейтинга в семестреЧтобы получить «4», нужно набрать 73 балла
Чтобы получить «5», нужно набрать 87 баллов
Чтобы получить зачет (допуск к зачету), нужно набрать 50
баллов
4.
Теоретическое программирование – математическаядисциплина, изучающая синтаксические и
семантические свойства программ, их структуру,
преобразования, процесс их составления и исполнения.
Основные направления теоретического
программирования:
- Математические основы программирования.
- Теория схем программ.
- Семантическая теория программ.
- Теория вычислительных процессов и структур.
- Прикладные задачи теоретического
программирования.
5.
Программа – формализованное описание процессаобработки данных
Цель программирования - описание процессов обработки данных .
Данные – представление фактов и идей в формализованном виде, пригодном
для передачи и обработки в некоем процессе.
Информация – смысл, который придается данным при их представлении.
Обработка данных – выполнение систематической последовательности
действий с данными.
Данные представляются и хранятся на носителях данных.
Информационная среда – совокупность носителей данных, используемых при
какой-либо обработке данных.
Состояние среды – набор данных, содержащихся в какой-либо момент в
информационной среде.
Процесс – последовательность сменяющих друг друга состояний некоторой
информационной среды.
Описать процесс - определить последовательность состояний заданной
информационной среды. Для того, чтобы этот процесс порождался
автоматически на компьютере, это описание должно быть формализованным.
Программа – формализованное описание процесса, необходимое для
автоматического порождения этого процесса на компьютере.
6.
Правильная программа – программа, которая несодержит ошибок, соответствует спецификации и дает
возможность формального вывода программы из
формального набора предпосылок
Надежная программа – программа, способная
безотказно выполнять определенные функции при
заданных условиях в течение заданного периода
времени с достаточно большой вероятностью.
Отказ в программе – появление в ней ошибки.
Степень надежности программы – вероятность работы
программы без отказа в течение определенного
периода времени.
7.
Основные математические понятияМножества
Множество-совокупность определенных и различных объектов (элементов).
Множество мы будем задавать явным перечислением, и заключать в
фигурные скобки. Например: D - множество дней недели: D = {Пн, Вт, Ср, Чт,
Пт, Сб, Вс}, D1 = {Вт, Ср, Чт, Пн, Сб, Пт, Вс}. D и D1 эквивалентны, т.е. порядок
элементов не важен.
Для бесконечных множеств используется характеристическое свойство А = {x |
p(x)}, где х – переменная, значениями которой являются некоторые объекты, а
р – свойство тех и только тех значений х, которые являются элементами
задаваемого множества.
8.
Основные математические понятияМножества
9.
Основные математические понятияМножества
10.
Основные математические понятияОтношения
11.
Основные математические понятияОтношения
12.
Основные математические понятияОтношения
13.
Основные математические понятияОтношения
14.
Основные математические понятияФункции
15.
Основные математические понятияФункции. Примеры отношений.
16.
Основные математические понятияФункции
17.
Основные математические понятияФункции
18.
Основные математические понятияГрафы
19.
Основные математические понятияГрафы
20.
Основные математические понятияВычислимость и разрешимость
Машина Тьюринга, перерабатывая начальные слова на ленте в заключительные, задает
словарную функцию, для которой начальные слова - значения аргумента, заключительные значения функции.
Изучая свойства программ и их математических абстракций – схем программ, мы ставим целью
автоматизацию программирования, в том числе автоматический анализ свойств программ и их
преобразования, осуществляемые с помощью других, специальных программ. Поэтому нас
интересуют алгоритмы, которые могли бы по любой предъявленной программе установить,
завершит ли она работу или будет «циклить», дают ли две программы, исходная и
оптимизированная, один и тот же результат, является ли программа синтаксически правильной
и т. д.
21.
Основные математические понятияВычислимость и разрешимость
В каждой машине Тьюринга есть две части:
1) неограниченная в обе стороны лента, разделенная на ячейки;
2) автомат (головка для считывания/записи, управляемая
программой).
С каждой машиной Тьюринга связаны два конечных алфавита:
алфавит входных символов A = {a0, a1, ..., am}
алфавит состояний Q = {q0, q1, ..., qp}.
Состояние q0 называется пассивным. Считается, что если
машина попала в это состояние, то она закончила свою работу.
Состояние q1 называется начальным. Находясь в этом
состоянии, машина начинает свою работу.
-
22.
Основные математические понятияВычислимость и разрешимость
23.
Основные математические понятияВычислимость и разрешимость
У машины Тьюринга есть три вида операций. Каждый раз для очередной пары (qj, ai)
машина Тьюринга выполняет команду, состоящую из трех операций с определенными
параметрами.
24.
Основные математические понятияВычислимость и разрешимость
После выполнения автоматом очередной команды он
переходит в состояние qm (которое может в частном случае
совпадать с прежним состоянием qj). Следующую команду
нужно искать в m-й строке таблицы на пересечении со
столбцом al (букву al автомат видит после сдвига).
Договоримся, что когда лента содержит входное слово, то
автомат находится против какой-то ячейки в состоянии q1.
В процессе работы автомат будет перескакивать из одной
клетки программы (таблицы) в другую, пока не дойдет до
клетки, в которой записано, что автомат должен перейти в
состояние q0. Эти клетки называются клетками останова.
Дойдя до любой такой клетки, машина Тьюринга
останавливается.
25.
Основные математические понятияВычислимость и разрешимость
26.
Машина Тьюринга. Пример.27.
Машина Тьюринга28.
Машина ТьюрингаМашина Тьюринга, перерабатывая начальные слова
на ленте в заключительные, задает словарную
функцию, для которой начальные слова - значения
аргумента, заключительные - значения функции.
Если машина не останавливается, начав работу с
некоторым словом на ленте, то функция, задаваемая
машиной, считается неопределенной для этого слова.
Таким образом, машина Тьюринга Т задает частичную
функцию FT и способ вычисления ее значений. Хотя
машины Тьюринга оперируют со словами, они могут
задавать и числовые функции в силу установленной
выше связи между словами и числами.
29.
30.
Характеристическая функция31.
Характеристическая функция32.
Программы и схемы программДля программиста задача, которая должна быть решена,
представляется как функция над множеством данных- объектов,
кодирующих заданную и искомую информацию.
Программа обладает всеми общими свойствами алгоритмов:
- является конструктивным объектом (представляет собой конечный
текст на некотором формализованном языке, который можно изучать
и преобразовывать методами формальной лингвистики),
- работает конечное время для тех наборов информации, для которых
вычислимая функция определена,
- обладает свойствами массовости и однозначности.
33.
Программы и схемы программВ начальной стадии программирования синтаксическая
сторона программирования выходит на первый план (этап
составления программы и первые фазы трансляции).
Каждая отдельная конструкция несет смысловую нагрузку –
это семантическая сторона программы.
Основные проблемы как практического программирования,
так и схем программ связаны с семантикой программ
(изучением и использованием тех свойств и
преобразований, которые сохраняют семантику и
инвариантны к синтаксису программы).
34.
Программы и схемы программПрограммные примитивы:
Теория схем программ должна учитывать (в отличие от теории алгоритмов)
структурный характер программ, особенности различных примитивов, их
взаимосвязь, возможность замены одних операций другими.
35.
Программы и схемы программСхемы программ -
это математические модели программ,
описывающие строение программы, то есть строение множества
программ, где конкретные операции и функции заменены абстрактными
функциональными и предикатными символами.
Требования к схемам программ:
- позволяют изучать свойства классов программ.
Сохраняют
все
интересующие
исследователя
свойства
рассматриваемого класса программ.
- Позволяют игнорировать несущественные свойства.
Модель модифицируема.
Структура модели изобразительно подобна структуре программы.
36.
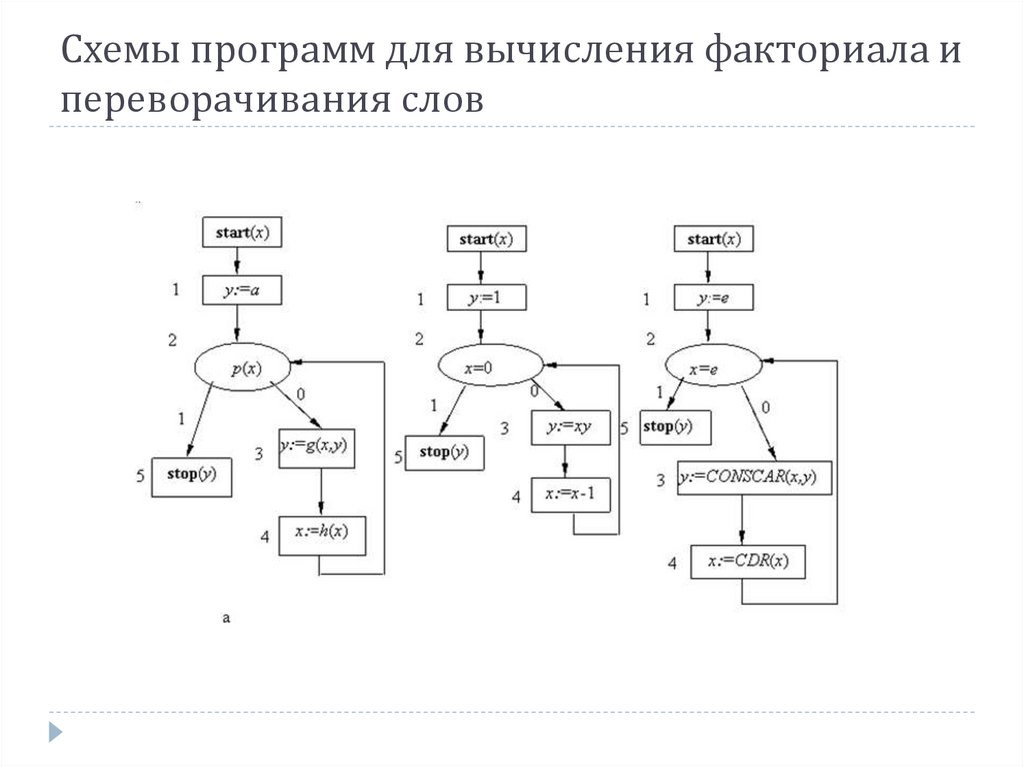
Программы и схемы программПример программы вычисления факториала n! и программы
переворачивания слов (поясняет различие между программами и
единой для них схемы S1.
Функция CONSCAR приписывает первую букву первого слова ко второму слову
(т. е. CONSCAR(аб, в) = ав), а функция CDR стирает первую букву слова(т. е.
CDR(аб) = б).
E – пустое слово
37.
Стандартные схемы программ (ССП) (текст нанекотором формальном языке, для которых не задана семантика
данных и операций)
Для стандартных схем программ отобраны:
Константы, простые переменные, выражения, операторы присваивания,
условные операторы, метки, переходы на метки.
Классы схем программ характеризуются базисом класса и структурой схем.
Полный базис В класса стандартных схем состоит из 4-х непересекающихся,
счетных множеств символов и множества операторов-слов, построенных из
этих символов.
Множества символов полного базиса:
Х = {x, х1, х2..., у, у1 у2..., z, z1, z2...} - переменные;
F = {f(0), f(1), f(2)..., g(0), g(1), g(2)..., h(0), h(1), h(2)...} - множество функциональных
символов(0-местные символы – константы);
Р = {р(0), р(1), р(2)...; q(0), q(1), q(2)...; } - множество предикатных символов(0местные символы – логические константы);
{start, stop, ...,:= и т. д.} - множество специальных символов.
38.
Стандартные схемы программ (ССП)Термами
(функциональными выражениями) называются
слова, построенные из переменных, функциональных и
специальных символов по следующим правилам:
1. Односимвольные слова, состоящие из переменных или
констант, являются термами;
2. Слово τ вида f(n)(τ1, τ2...τn), где τ1, τ2...τn - термы, является
термом;
3. Те и только те слова, о которых говорится в п.п. 1,2,
являются термами.
Примеры: х, f(0), а, f(1)(х), g(2)(x, h(3)(y, a)).
Тестами
(логическими выражениями) называются
логические константы и слова вида р(n)(τ1, τ2,...,τn).
Примеры: p(0), p(0)(х), q(3)(x, y, z), p(2) (f(2(x, y)).
39.
Стандартные схемы программ (ССП)Множество операторов включает пять типов:
1.
2.
3.
4.
5.
начальный оператор - слово вида start(х1, х2...хк), где k
≥0, а х1, х2...хк - переменные, называемые результатом
этого оператора;
заключительный оператор - слово вида stop(τ1, τ2...τn),
где n ≥0, а τ1, τ2...τn - термы; вхождения переменных в
термы τ называются аргументами этого оператора;
оператор присваивания - слово вида х := τ, где х –
переменная (результат оператора), а τ - терм;
вхождения переменных в термы называются
аргументами этого оператора;
условный оператор (тест) - логическое выражение;
вхождения переменных в логическое выражение
называются аргументами этого оператора;
оператор петли - односимвольное слово loop.
40.
Подклассы используют ограниченные базисы.Подкласс V1 имеет базис:
{х1, х2}, {а, f(1)}, {p(1)}, {start, stop, (,),:=, ,}
В этом базисе написана схема:
{start(х1, х2);
х1:=f(x1), x2:=f(x2),
x1:=а, х2:= а, р(х1), р(х2),
stop(х1, х2)},
Cхемы из этого подкласса используют две переменные,
константу а, один одноместный функциональный символ,
один предикатный символ и операторы указанного вида.
41.
Пример базисаПеременные {x,y}.
Функциональные символы {g(2) ,h(1) , a(0)}
Предикатные символы {p(1)}
Специальные символы {begin, end, if, then, goto, L1,L2}
42.
Графовая форма (ССП)Стандартной схемой в базисе В называется конечный
(размеченный ориентированный) граф без свободных дуг и с
вершинами следующих пяти видов:
1.
Начальная вершина (ровно одна) помечена начальным
оператором. Из нее выходит ровно одна дуга. Нет дуг,
ведущих к начальной вершине.
2.
Заключительная вершина (может быть несколько). Помечена
заключительным оператором. Из нее не выходит ни одной
дуги.
3.
Вершина-преобразователь. Помечена оператором
присваивания. Из нее выходит ровно одна дуга.
4.
Вершина-распознаватель. Помечена условным оператором
(называемым условием данной вершины). Из нее выходит
ровно две дуги, помеченные 1 (левая) и 0 (правая).
5.
Вершина-петля. Помечена оператором петли. Из нее не
выходит ни одной дуги.
43.
Графовая форма (ССП)Конечное множество переменных схемы S составляют ее память ХS.
Из определения следует, что один и тот же оператор может помечать несколько вершин
схемы.
Вершины именуются метками вершины - целым неотрицательным числом(0, 1, 2,...).
Начальная вершина всегда помечается меткой 0.
Говорят, что переменная x задана на дуге е схемы S, если любой путь в S,
начинающийся начальной вершиной и кончающийся дугой е, содержит хотя бы один
оператор с результатом x.
Схема S называется правильной, если на каждой ее дуге заданы все переменные, т.е. в
схеме используются все переменные из множества переменных базиса схемы.
Вершины-преобразователи изображаются прямоугольниками, а вершинараспознаватель - овалом. Операторы записываются внутри вершины.
44.
Линейная форма (ССП)Для использования линейной формы СПП множество специальных символов
расширим дополнительными символами {:, goto, if, then, else}.
СПП в линейной форме представляет собой последовательность инструкций,
которая строится следующим образом:
если выходная дуга начальной вершины ведет к вершине L, то начальной
вершине соответствует инструкция:
0: start(х1,..., хn) goto L;
если вершина L - преобразователь (х:=τ) и выходная дуга ведет к L1, то
L: x: =τ goto L1;
если вершина L – заключительная вершина, то
L: stop(τ1,..., τm);
если вершина с меткой L - распознаватель, причем 1-дуга ведет к вершине L1,
а 0-дуга - к вершине L0, то:
L: if р(τ1,...τk) then L1 else L0;
если вершина с меткой L - петля, то ей соответствует инструкция
L: loop.
45.
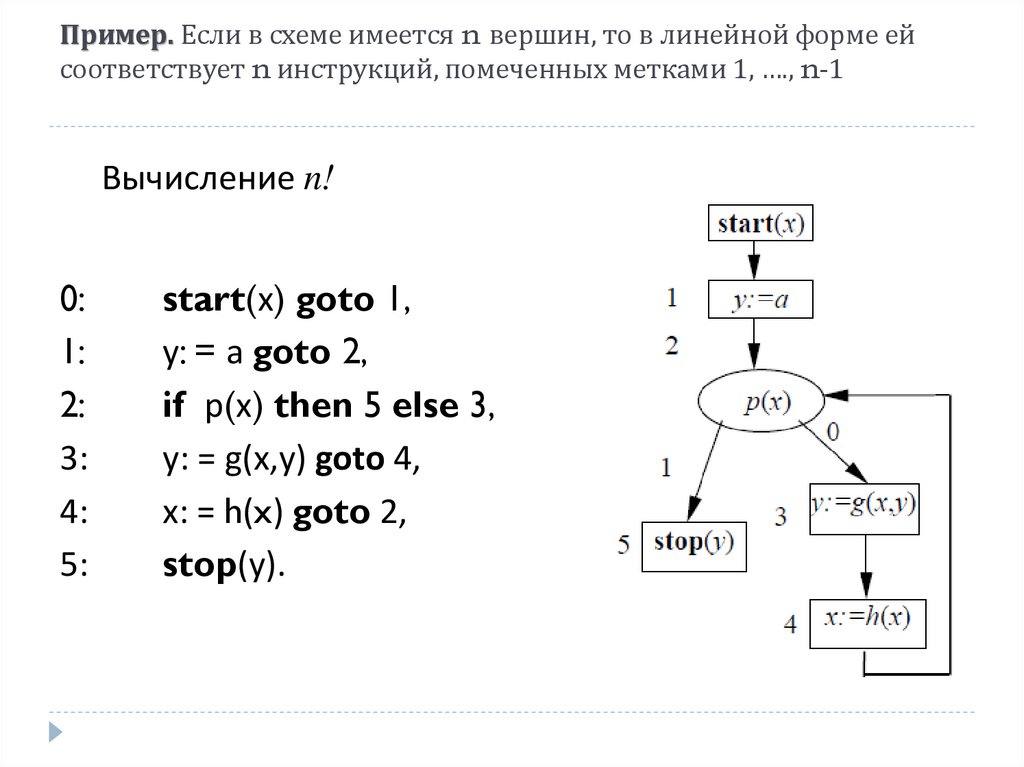
Пример. Если в схеме имеется n вершин, то в линейной форме ейсоответствует n инструкций, помеченных метками 1, …., n-1
Вычисление n!
0:
1:
2:
3:
4:
5:
start(х) goto 1,
у: = а goto 2,
if р(х) then 5 else 3,
у: = g(x,y) goto 4,
х: = h(x) goto 2,
stop(у).
46.
Схемы программ для вычисления факториала ипереворачивания слов
47.
Интерпретация стандартных схем программСтандартная схема не является записью алгоритма, с
ее помощью можно исследовать только структурные
свойства программы (семантика вычислений не
исследуется).
Способом исследования содержательной теории схем
построение интерпретированной схемы программы.
48.
Интерпретация стандартных схем программПусть в некотором базисе В определен класс ССП.
Интерпретацией базиса В в области интерпретации D
называется функция I, которая сопоставляет:
1.
2.
3.
4.
5.
Каждой переменной х из базиса В - некоторый элемент
d = I(x) из области интерпретации D;
Каждой константе а из базиса В - некоторый элемент
d = I(а) из области интерпретации D;
Каждому функциональному символу f(n) - всюду
определенную функцию F(n)=I(f(n));
Каждой логической константе р(0) - один символ множества
{ 0,1 };
Каждому предикатному символу р(n) - всюду определенный
предикат P(n) = I(p(n)).
Пара (S,I) называется интерпретированной стандартной схемой
(ИСС), или стандартной программой (СП).
49.
Выполнение программыСостоянием памяти программы (S,I) называют функцию
W: XS D, которая каждой переменной x из памяти схемы S
сопоставляет элемент W(x) из области интерпретации D.
Значение терма τ при I и состоянии памяти W (τI(W))
определяется :
1. если τ=х, x – переменная, то τI(W) = W(x);
2. если τ=a, a – константа, то τI(W) = I(a);
3. если τ=f(n)(τ1, τ2..., τn), то
τI(W)= I(f(n))(τ1I(W), τ2I(W),..., τnI(W)).
Значение теста π при интерпретации I и состоянии памяти W
или π I(W):
если π = π(n)(τ1, τ2..., τn),
то pI(W)= I(π(n))(τ1I(W), τ2I(W),... τnI(W)), n ≥0.
50.
Конфигурация программыКонфигурация программы - пара U=(L,W), где L - метка
вершины схемы S, а W - состояние ее памяти.
Выполнение программы описывается конечной или
бесконечной последовательностью конфигураций,
которую
называют
протоколом
выполнения
программы (ПВП).
51.
Протокол выполнения программыПротокол (U0, U1,..., Ui, Ui+1,...) выполнения программы
(S,I) определяем следующим образом (Ui=(ki,Wi)):
U0=(0, W0), W0 – начальное состояние памяти схемы S
при интерпретации I.
Пусть Ui=(ki, Wi) - i-я конфигурация ПВП, а О - оператор
схемы S в вершине с меткой ki.
Если О - stop(τ1, τ2... τn), то Ui - последняя конфигурация.
В этом случае считают, что, программа (S,I)
останавливается, а последовательность значений
τ1I(W), τ2I(W),..., τnI(W) объявляют результатом val(S,I)
выполнения программы (S,I).
52.
Протокол выполнения программыЕсли О - не заключительный оператор, в протоколе имеется
следующая, (i+1)-я конфигурация Ui+1 = (ki+1, Wi+1), причем
a)
если О - начальный оператор, а выходящая из него дуга
ведет к вершине с меткой L, то ki+1 = L и Wi+1 = Wi;
b)
если О - оператор присваивания х:=τ, а выходящая из
него дуга ведет к вершине с меткой L, то ki+1 = L, Wi+1 = Wi,
Wi+1(х) = τ1(Wi);
c)
если О - условный оператор p и pI(Wi) = Δ, где Δϵ{0,1}, а
выходящая из него дуга ведет к вершине с меткой L, то
ki+1 = L и Wi+1 = Wi;
d) если О - оператор петли, то ki+1 = L и Wi+1 = Wi, так что
протокол бесконечен.
53.
Пример (вычислние 4!)Программа (S,I) вычисляет 4!
Интерпретация (S, I) задана так:
1.
область интерпретации D1 подмножество множества
Nat целых неотрицательных
чисел;
2.
I(x)=4; I(y)=0; I(a)=1;
3.
I(g)=G, где G - функция
умножения чисел, т. е.
G(d1,d2)= d1*d2;
4.
I(h)=H, где H - функция
вычитания единицы, т. е.
H(d)= d-1;
5.
I(p)=P, где P - предикат
«равно 0», т.е. P(d)=1, если
d=0.
54.
ПримерПрограмма (S,I) вычисляет 4!
Конфигурация U0 U1 U2 U3 U4 U5 U6 U7 U8 U9 U10 U11 U12 U13
Метка
Значения
х
у
0
4
0
1
4
1
2
4
1
3
4
4
4
3
4
2
3
4
3 4 2 3 4 2 3
3 2 2 2 1 1 1 0
12 12 12 24 24 24 24 24
55.
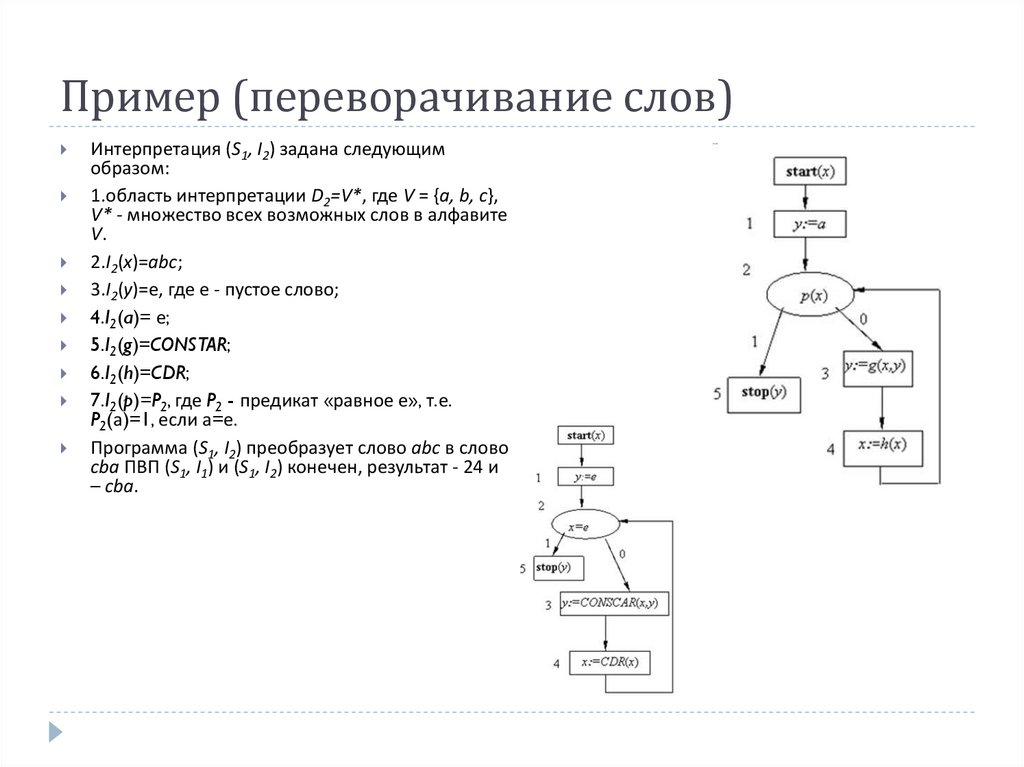
Пример (переворачивание слов)Интерпретация (S1, I2) задана следующим
образом:
1.область интерпретации D2=V*, где V = {a, b, c},
V* - множество всех возможных слов в алфавите
V.
2.I2(x)=abc;
3.I2(y)=e, где e - пустое слово;
4.I2(a)= e;
5.I2(g)=CONSTAR;
6.I2(h)=CDR;
7.I2(p)=P2, где P2 - предикат «равное e», т.е.
P2(a)=1, если a=e.
Программа (S1, I2) преобразует слово abc в слово
cba ПВП (S1, I1) и (S1, I2) конечен, результат - 24 и
– cba.
56.
Пример (переворачивание слов)57.
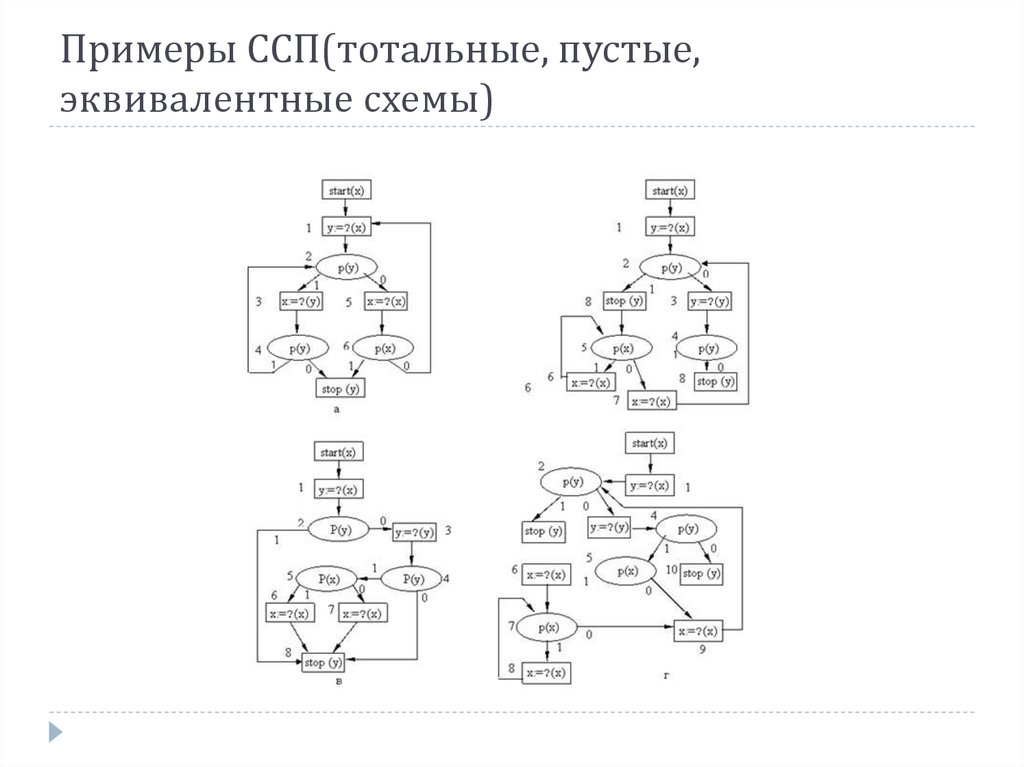
Свойства и виды ССПССП S в базисе В тотальна (пуста), если для любой
интерпретации I базиса В программа (S, I)
останавливается (зацикливается).
Стандартные схемы S1 и S2 в базисе В функционально
эквивалентны (S1 ~ S2), если либо обе зацикливаются,
либо обе останавливаются с одинаковым результатом,
т. е. val (S1, I) » val (S2, I).
58.
Примеры ССП(тотальные, пустые,эквивалентные схемы)
59.
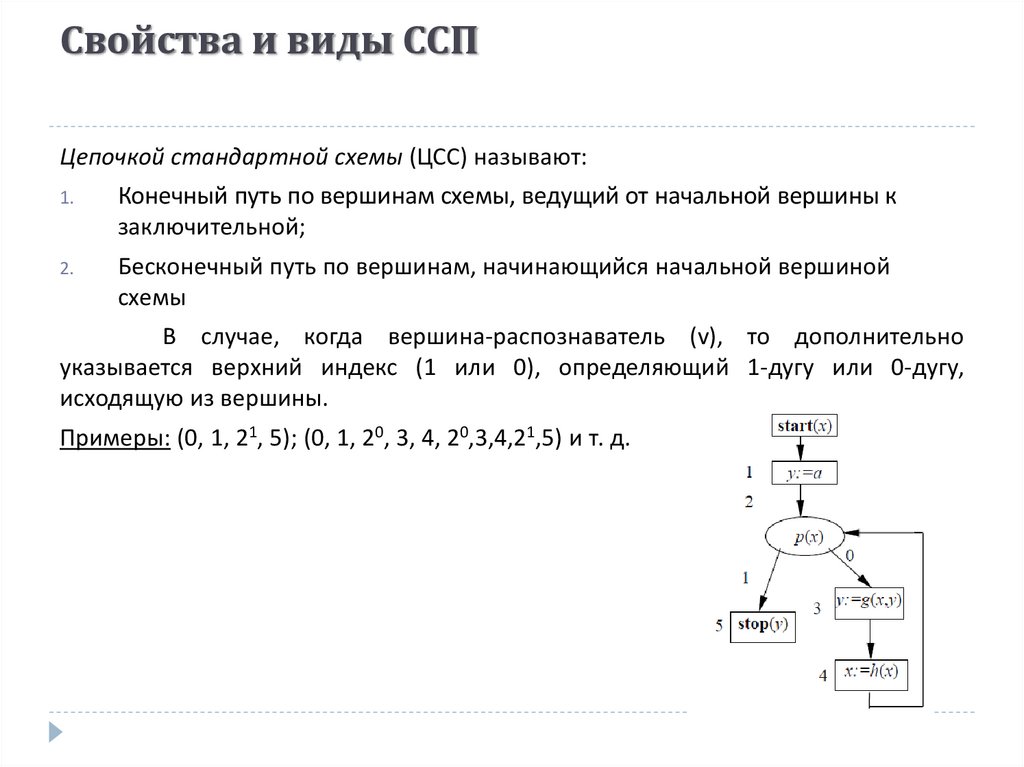
Свойства и виды ССПЦепочкой стандартной схемы (ЦСС) называют:
1.
Конечный путь по вершинам схемы, ведущий от начальной вершины к
заключительной;
2.
Бесконечный путь по вершинам, начинающийся начальной вершиной
схемы
В случае, когда вершина-распознаватель (v), то дополнительно
указывается верхний индекс (1 или 0), определяющий 1-дугу или 0-дугу,
исходящую из вершины.
Примеры: (0, 1, 21, 5); (0, 1, 20, 3, 4, 20,3,4,21,5) и т. д.
60.
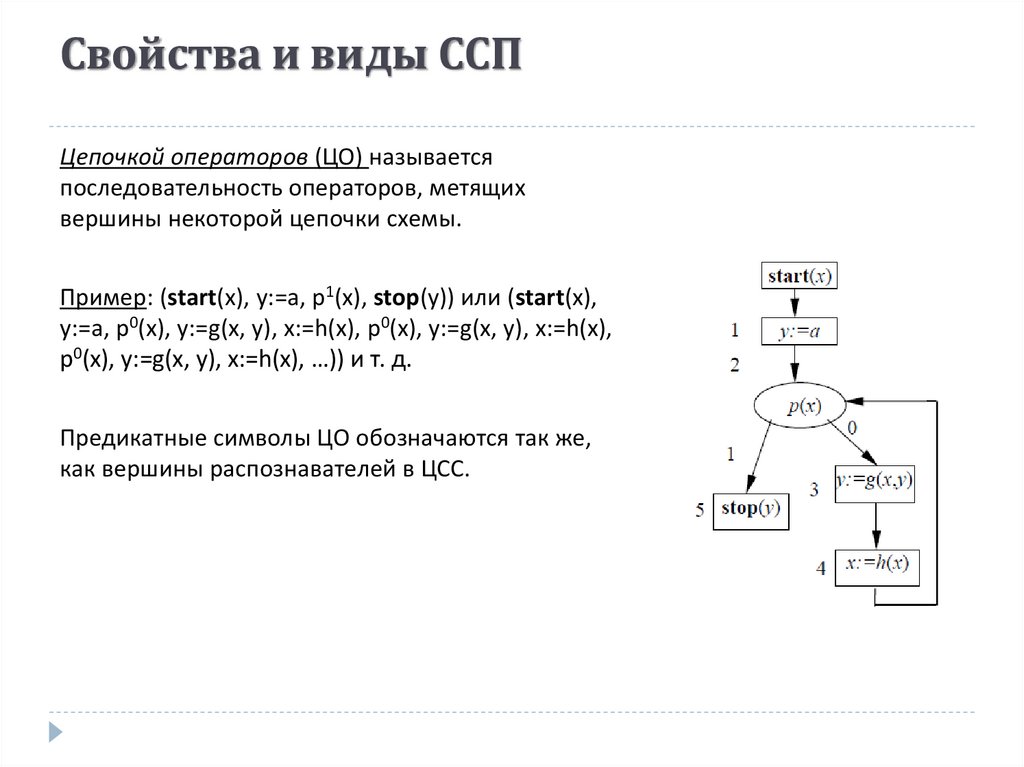
Свойства и виды ССПЦепочкой операторов (ЦО) называется
последовательность операторов, метящих
вершины некоторой цепочки схемы.
Пример: (start(х), у:=a, р1(x), stop(у)) или (start(х),
у:=a, р0(x), y:=g(x, y), x:=h(x), р0(x), y:=g(x, y), x:=h(x),
р0(x), y:=g(x, y), x:=h(x), …)) и т. д.
Предикатные символы ЦО обозначаются так же,
как вершины распознавателей в ЦСС.
61.
Свойства и виды ССПЦСС в базисе В называют допустимой, если она
подтверждается хотя бы одной интерпретацией этого
базиса.
62.
Свойства и виды ССПССП свободна, если все ее цепочки допустимы.
Допустимая цепочка операторов - это цепочка
операторов, соответствующая допустимой цепочке
схемы. В тотальной схеме все допустимые цепочки (и
допустимые цепочки операторов) конечны. В пустой
схеме - бесконечны.
63.
Свободные интерпретации (СИ)Все СИ базиса В имеют одну и ту же область интерпретации,
которая совпадает со множеством Т всех термов базиса В.
Все СИ одинаково интерпретируют переменные и
функциональные символы, а именно:
1. для любой переменной х из базиса В и для любой СИ Ih
этого базиса Ih(x)=x;
2. для любой константы a из базиса В Ih(a)=a;
3. для любого функционального символа f(n) из базиса В,
где n>=1, Ih(f(n))=F(n): Tn T, где F(n) - словарная функция
такая, что
F(n)(t1, t2, ..., tn)= f(n) (t1, t2, ... tn),
т. е. функция F(n) по термам t1, t2, ...tn из Т строит новый терм,
используя функциональный смысл символа f(n).
Интерпретации предикатных символов - полностью
свободна, т.е. разные СИ различаются лишь интерпретаций
предикатных символов.
64.
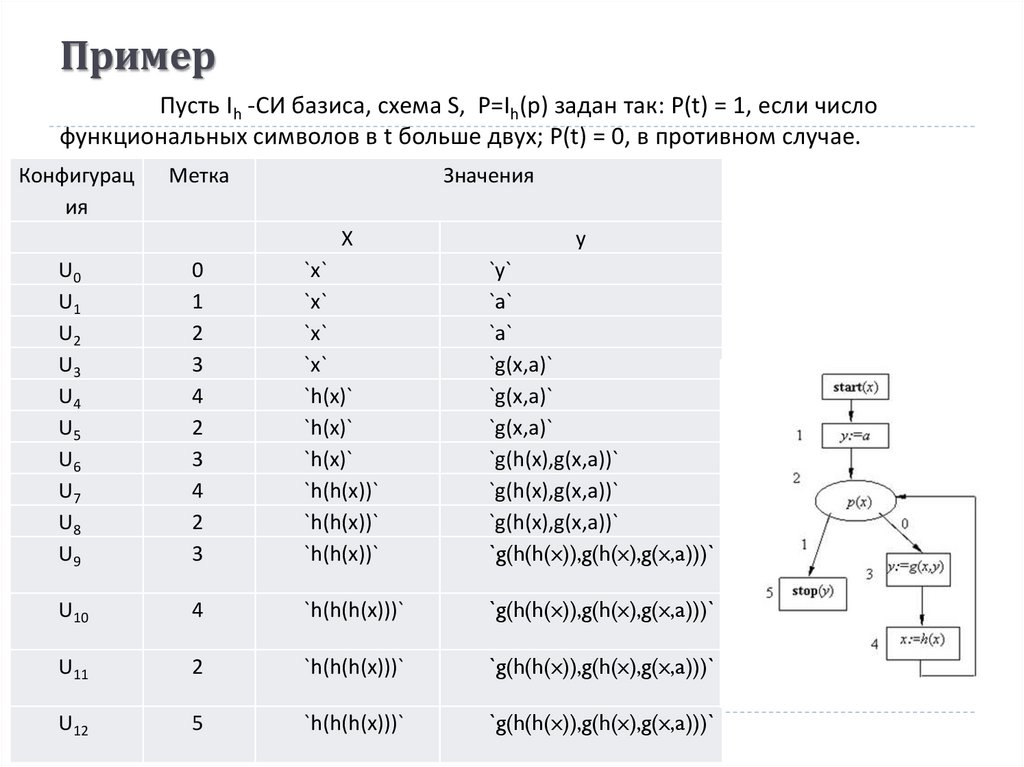
ПримерПусть Ih -СИ базиса, схема S, Р=Ih(р) задан так: P(t) = 1, если число
функциональных символов в t больше двух; P(t) = 0, в противном случае.
Конфигурац
ия
Метка
Значения
X
у
U0
U1
U2
U3
U4
U5
U6
U7
U8
U9
0
1
2
3
4
2
3
4
2
3
`x`
`x`
`x`
`x`
`h(x)`
`h(x)`
`h(x)`
`h(h(x))`
`h(h(x))`
`h(h(x))`
`y`
`a`
`a`
`g(x,a)`
`g(x,a)`
`g(x,a)`
`g(h(x),g(x,a))`
`g(h(x),g(x,a))`
`g(h(x),g(x,a))`
`g(h(h(x)),g(h(x),g(x,a)))`
U10
4
`h(h(h(x)))`
`g(h(h(x)),g(h(x),g(x,a)))`
U11
2
`h(h(h(x)))`
`g(h(h(x)),g(h(x),g(x,a)))`
U12
5
`h(h(h(x)))`
`g(h(h(x)),g(h(x),g(x,a)))`
65.
Примерg(2)(h(1)(x), g(2)(x,y)) - бесскобочный терм ghxgxy (получается
путем удаления из исходного терма всех скобок и запятых).
Правила восстановления терма по бесскобочной записи
аналогичны правилам восстановления арифметических по их
прямой польской записи.
Примеры
A*B => AB*
A*B+C =>AB*C+
A*(B+C/D)
=>ABCD/+* A*B+C*D =>AB*CD*+
Правила представления в польской записи:
1. Идентификаторы следуют в том же порядке, что и в
инфиксной записи
2. Операторы следуют в том же порядке, в каком они
должны вычисляться (слева направо)
3. Операторы располагаются непосредственно за своими
операндами.
66.
Согласованные свободные интерпретацииИнтерпретация I и СИ Ih (того же базиса В) согласованы,
если для любого логического выражения p справедливо
Ih(p)=I(p).
Если интерпретация I и свободная интерпретация Ih
согласованы, то программы (S, I) и (S, Ih) либо
зацикливаются, либо обе останавливаются и I(val(S,Ih))=
val(S,I), т.е. каждой конкретной программе можно
поставить во взаимно-однозначное соответствие
свободно интерпретированную (стандартную)
согласованную программу
67.
68.
Согласованные свободные интерпретацииТеорема Лакхэма – Парка – Паттерсона. Стандартные
схемы S1 и S2 в базисе В функционально эквивалентны
тогда и только тогда, когда они функционально
эквивалентны на множестве всех свободных
интерпретаций базиса В, т.е. когда для любой
свободной интерпретации Ih программы (S1,Ih) и (S2,Ih)
либо обе зацикливаются, либо обе останавливаются и
val(S1,I) = {I(val(S1 Ih)) = I(val(S2 Ih))} = val(S2,I).
69.
Согласованные свободные интерпретацииСтандартная схема S в базисе В пуста (тотальна,
свободна) тогда и только тогда, когда она пуста
(тотальна, свободна) на множестве всех свободных
интерпретаций этого базиса, т.е. если для любой
свободной интерпретации Ih программа (S, Ih)
зацикливается (останавливается).
Стандартная схема S в базисе В свободна тогда и
только тогда, когда она свободна на множестве всех
свободных интерпретаций этого базиса, т. е. когда
каждая цепочка схемы подтверждается хотя бы одной
свободной интерпретацией.
70.
Рекурсивные схемы программВычисление факториала
Рекурсивно определяемая функция
FACT(х) = 1,если х = 0,
FACT(х) = х *FACT(х — 1), если х > 0.
Программа(рекурсивный язык, базирующийся на
механизме рекурсивных функций языка Паскаль)
FACT(a),
FACT(х) = if х = 0 then 1 else х * FACT(х - 1),
где а — некоторое целое неотрицательное число.
71.
Рекурсивные схемы программ. Выполнениепрограммы.
Программа(рекурсивный язык, базирующийся на механизме
рекурсивных функций языка Паскаль)
FACT(a),
FACT(х) = if х = 0 then 1 else х * FACT(х - 1),
где а — некоторое целое неотрицательное число.
72.
Рекурсивная схемаПолный базис РС включает четыре счетных множества
символов: переменные, функциональные символы,
предикатные символы, специальные символы.
Множество специальных символов : {if, то, else, (, ), ,}.
Отличие от ССП: множество функциональных символов
разбито на два непересекающиеся подмножества:
множество базовых функциональных символов и
множество определяемых функциональных символов
(обозначаются прописными буквами, например, F(1),G(2), и
т.д.).
В базисе РС нет множества операторов, вместо него –
множество логических выражений и множество термов.
73.
Термы в РСПростые термы (Термами (функциональными выражениями) называются
слова, построенные из переменных, функциональных и специальных
символов по определенным правилам)
Базовые термы (относятся к простым термам) - не содержат определяемых
функциональных символов.
Вызовы-термы вида F(n)(t1,t2,…tn), где t1,t2,…t n - простые термы, F(n) определяемый функциональный символ.
Логическое выражение - слово вида p(n)(t1,t2,…tn),
Терм - это простой терм, или условный терм, т.е. слово вида
if p then t1 else t2,
где p - логическое выражение, t1, t2 - простые термы, называемые левой и
соответственно правой альтернативой.
Примеры термов:
f(x, g(x, y)); h(h(a)) - базовые термы;
f(F(x), g(x, F(y))); H(H(a)) - простые термы;
F(x); H(H(a)) - вызовы;
If p(x, y) then h(h(a)) else F(x) - условный терм.
74.
Рекурсивное уравнениеРекурсивным уравнением, или определением функции F
назовем слово вида F(n)(x1,x2,…xn) = t(x1,x2,…xn),
где t(x1,x2,…xn) - терм, содержащий переменные,
называемые формальными параметрами функции F.
Рекурсивной схемой называется пара (t, М), где t - терм,
называемый главным термом схемы (или ее входом). М такое множество рекурсивных уравнений, что все
определяемые функциональные символы в левых частях
уравнений различны и всякий определяемый символ,
встречающийся в правой части некоторого уравнения или в
главном терме схемы, входит в левую часть некоторого
уравнения.
75.
Рекурсивная схемаПример РС:
RS1: F(x); F(x) = if p(x) then a else g(x, F(h(x))).
RS3: F(x); F(x) = if p(x) then x else f(F(g(x)), F(h(x))).
Пара (RS, I), где RS - PC в базисе В, а I - интерпретация
этого базиса, называется рекурсивной программой.
При этом заметим, что определяемые
функциональные символы не интерпретируются.
FACT(a),
FACT(х) = if х = 0 then 1 else х * FACT(х - 1),
где а — некоторое целое неотрицательное число.
76.
Рекурсивная программаПара (S,I), где S – рекурсивная схема в базисе β, а I –
интерпретация этого базиса, называется рекурсивной
программой.
Выполнение рекурсивной программы определяется с
помощью протокола выполнения, который
представляет собой конечную или бесконечную
последовательность конфигураций.
Конфигурации определяются с помощью понятия
значения терма.
77.
Рекурсивная программа78.
Рекурсивная программа79.
ПримерRS1:
F(x); F(x) = if p(x) then a else g(x, F(h(x))).
80.
Свободная интерпретацияRS1:
F(x); F(x) = if p(x) then a else g(x, F(h(x))).
81.
Задания на практическую работу №31). Постройте протокол выполнения рекурсивной программы для
следующей рекурсивной схемы:
RS3: F(x); F(x) = if p(x) then x else f(F(g(x)), F(h(x))).
2).
3).Построить двухголовочный автомат, допускающий слова в алфавите
(а,х), в которых количество букв а и х одинаково.
Построить соответствующий двухголовочному автомату двоичный
автомат и ССП этого двоичного автомата.
82.
Схемы с процедурамиСхемы с процедурами
главная схема
множество схем процедур
Главная схема - это стандартная схема, в которой
имеются операторы присваивания специального вида
x:= F(n)(y1,y2,…yn), называемые операторами вызова
процедур, где x, y1,y2,…yn – переменные, F(n)определяемый функциональный символ.
Схема процедуры состоит из заголовка и тела
процедуры, разделенных символом равенства.
Заголовок имеет тот же вид, что и левая часть
рекурсивных уравнений. Тело процедуры - это
стандартная схема того же вида, что и главная схема.
83.
Схемы с процедурами84.
Выполнение интерпретированных схем спроцедурами
85.
Моделирование ССПВычислимая функция - функция, вычисление значений
которой может быть проведено с помощью заранее
заданной эффективной процедуры, или алгоритма.
Автоматы
Одноленточные автоматы
Многоленточные автоматы
Двухголовочные автоматы
86.
Одноленточный автомат (ОКА)ОКА задается набором A = { V, Q, R, q0, #, I } и правилом
функционирования.
V - алфавит;
Q - множество состояний (QᴖV=ᴓ);
R - множество заключительных состояний (RϵQ);
q0 - выделенное начальное состояние;
I - программа автомата;
# - «пустой» символ.
Программа автомата I представляет собой множество
команд вида qа q', в которой q, q' ϵQ, a €V и для любой
пары (q, a) существует единственная команда,
начинающаяся этими символами.
87.
Одноленточный автомат (ОКА)Особенности одноленточного автомата:
выделены заключительные состояния;
машина считывает символы с ленты, ничего не
записывая на нее;
на каждом шаге головка автомата, считав символ с
ленты и перейдя согласно программе в новое
состояние, обязательно передвигается вправо на одну
клетку;
автомат останавливается в том и только в том случае,
когда головка достигнет конца слова, т.е. символа #.
88.
Одноленточный автомат (ОКА)Автомат допускает слово a в алфавите V, если, начав работать с
лентой, содержащей это слово, он останавливается в
заключительном состоянии.
Разреши́ мое множество (также рекурси́вное, вычислимое) —
для которого существует алгоритм, получающий на вход
любое слово и через конечное число шагов завершающийся
определением, принадлежит ли оно данному множеству.
Другими словами, множество является разрешимым, если
его характеристическая функция вычислима. Множество, не
являющееся разрешимым, называется неразреши́мым.
Автомат A задает характеристическую функцию множества MA
допускаемых им слов в алфавите V, т. е. он распознает,
принадлежит ли заданное слово множеству MA если связать с
остановкой в заключительном состоянии символ 1, а с
остановкой в незаключительном состоянии – 0.
89.
Одноленточный автомат (ОКА)Множество вершин – множество состояний Q;
Из вершины q в вершину q’ ведет дуга,
помеченная символом а, тогда и только тогда,
когда программа автомата содержит команду
qа q'.
Работе автомата над заданным словом
соответствует путь из начальной вершины q0.
Последовательность проходимых вершин этого
пути – это последовательность принимаемых
автоматом состояний, образ пути по дугам –
читаемое слово.
Любой путь в графе автомата, начинающийся в
вершине q0 и заканчивающийся в вершине q’ϵR,
порождает слово, допустимое автоматом.
90.
ПримерОКА A = ({a, b}, {q0, q1, q2, q3}, {q2}, q0, #, I),
допускающего слова {an bm | n=1,2, ...; m=1,2, ...},
задается графом. Программа I содержит команды:
q0a q1; q0b q3; q1a q1; q1b q2; q2a q3; q2b q2;
q3a q3; q3b q3.
Пример слова допускающего: aabb
Пример слова недопускающего: aba
91.
Одноленточный автомат (ОКА)Автомат называется пустым, если МА =ᴓ.
Автоматы А1 и А2 эквивалентны, если МА1 = МА2.
Для ОКА доказано:
Проблема пустоты ОКА разрешима.
Проблема эквивалентности ОКА разрешима.
92.
Многоленточные автоматы (МКА)МКА задается A = { V, Q, R, q0, #, I } , где множество
состояний Q разбивается на n ≥ 2 непересекающихся
подмножеств Q1, ..., Qn.
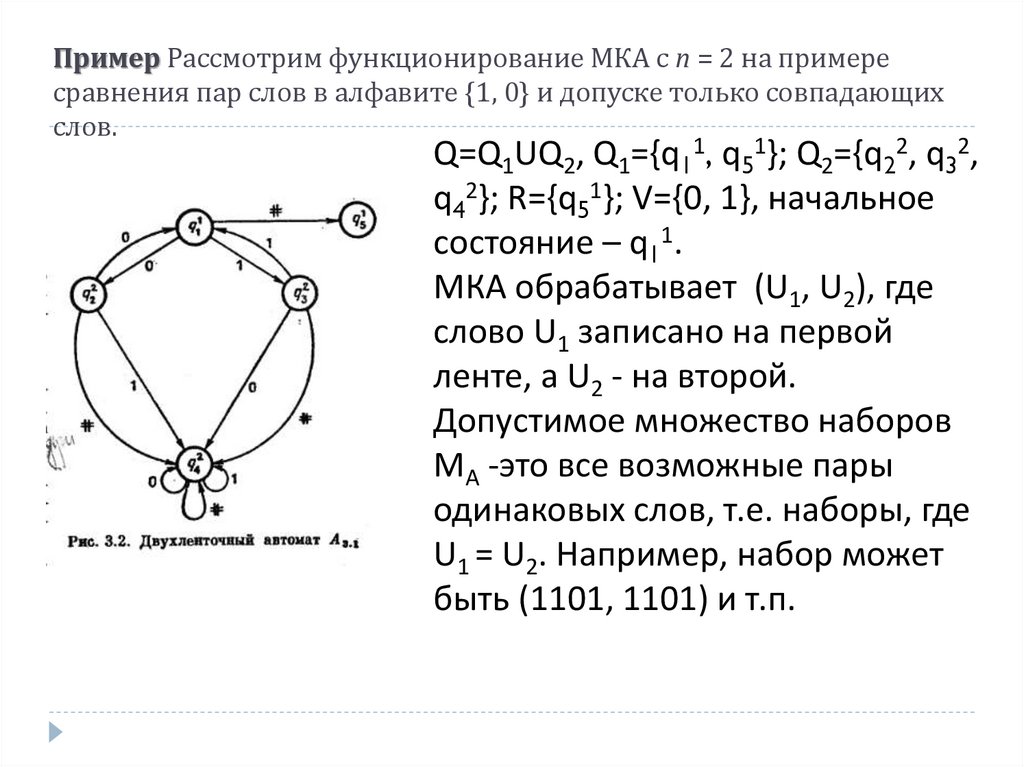
93.
Пример Рассмотрим функционирование МКА с n = 2 на примересравнения пар слов в алфавите {1, 0} и допуске только совпадающих
слов.
Q=Q1UQ2, Q1={q11, q51}; Q2={q22, q32,
q42}; R={q51}; V={0, 1}, начальное
состояние – q11.
МКА обрабатывает (U1, U2), где
слово U1 записано на первой
ленте, а U2 - на второй.
Допустимое множество наборов
MA -это все возможные пары
одинаковых слов, т.е. наборы, где
U1 = U2. Например, набор может
быть (1101, 1101) и т.п.
94.
Двухголовочные автоматыДвухгогловочные автоматы имеют одну ленту и две головки,
которые могут перемещаться вдоль ленты в одном
направлении.
Множество состояний Q разбито на два непересекающихся
множества. В состояниях Q1 активна первая головка, а в
состояниях Q2 - вторая.
95.
Двухголовочные автоматыПример
Находясь в состоянии g01, автомат передвигает
первую головку к началу второго слова и, обнаружив
его, переходит в состояние q11. Если конец ленты #
встречается раньше символа *, автомат переходит в
незаключительное состояние q62. Если же автомат
приходит к состоянию q11, он считывает поочередно
символы второго слова первой головкой (состояние
q11), а символы первого слова — второй головкой
(состояния q32 и q52), сравнивая эти символы. Автомат
возвращается каждый раз в состояние q11, если
символы одинаковы.
96.
Двухголовочные автоматы (ДКА)97.
Двухголовочные автоматы (ДКА)98.
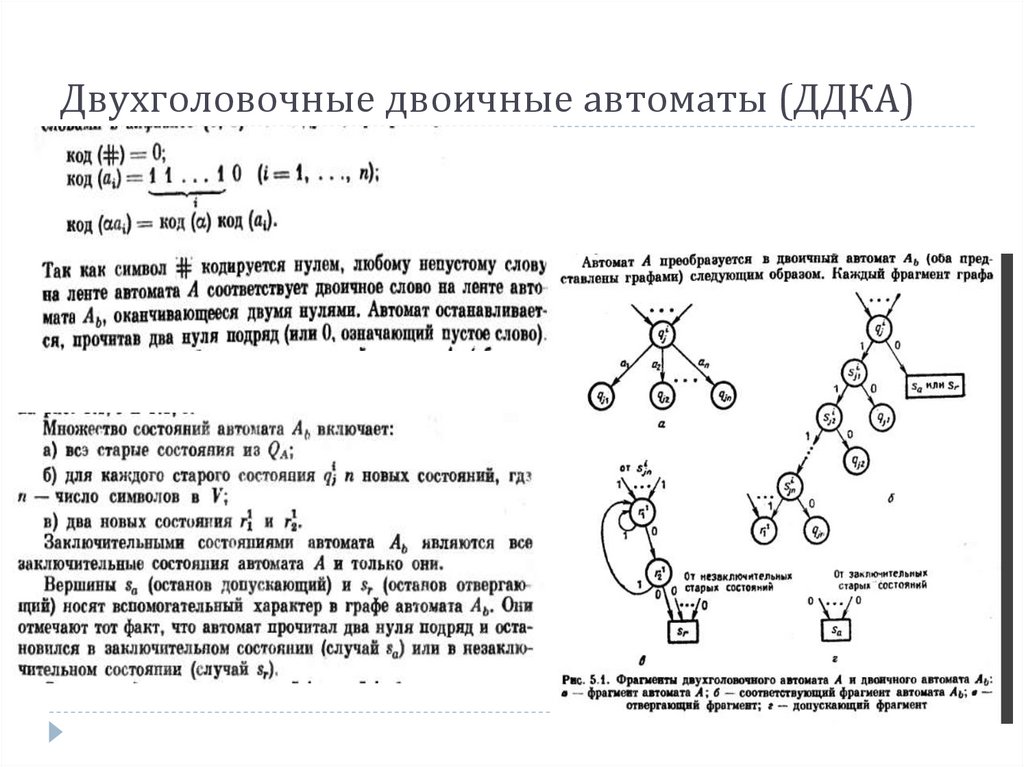
Двухголовочные двоичные автоматы (ДДКА)99.
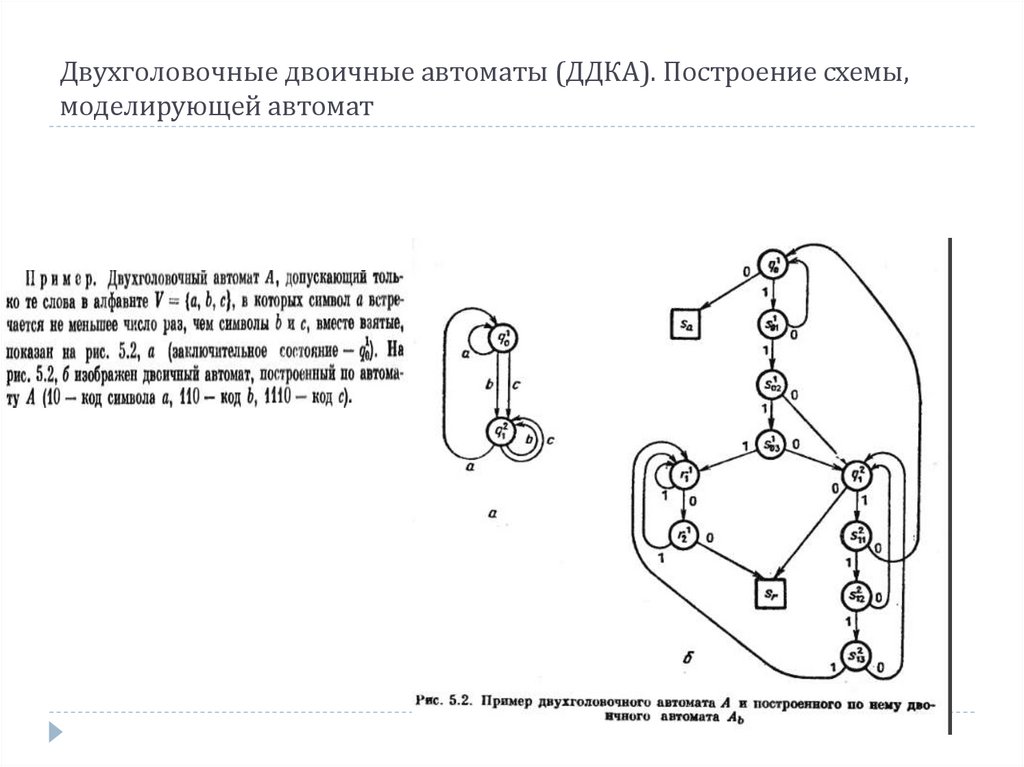
Двухголовочные двоичные автоматы (ДДКА). Построение схемы,моделирующей автомат
100.
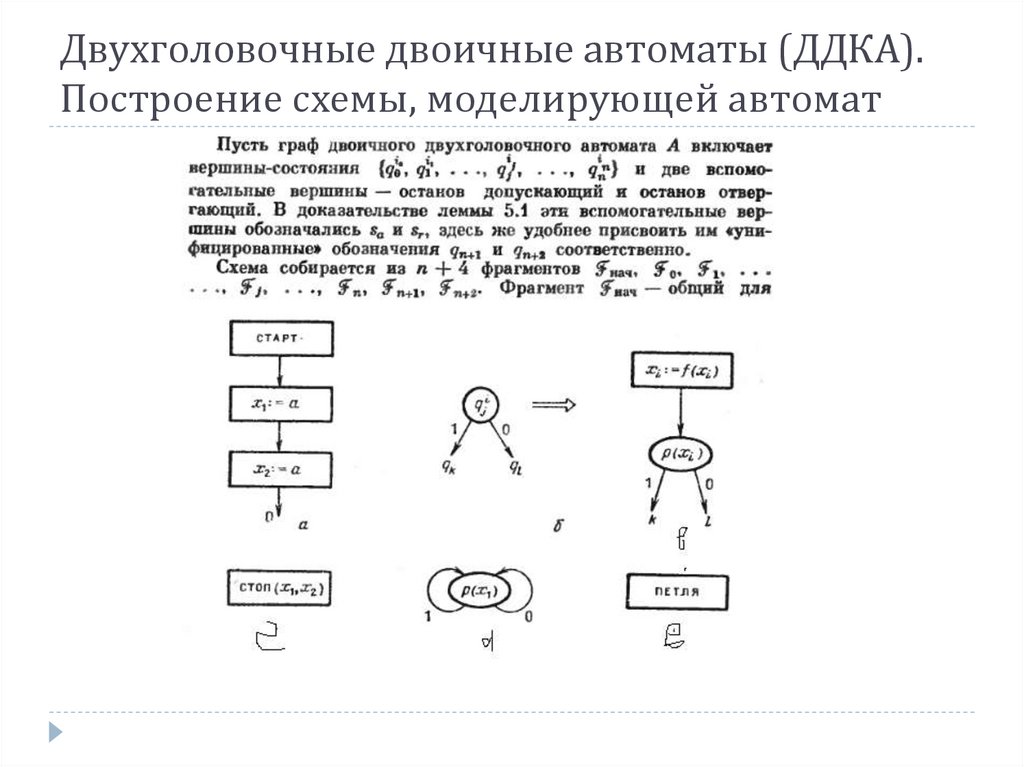
Двухголовочные двоичные автоматы (ДДКА).Построение схемы, моделирующей автомат
101.
Двухголовочные двоичные автоматы (ДДКА).Построение схемы, моделирующей автомат
102.
Двухголовочные двоичные автоматы (ДДКА).Построение схемы, моделирующей автомат



























































































 informatics
informatics








