Система двух случайных величин. Повторение (материал прошлой пары)

1.

Повторение (материал прошлой пары)
Система двух случайных величин
1

2.

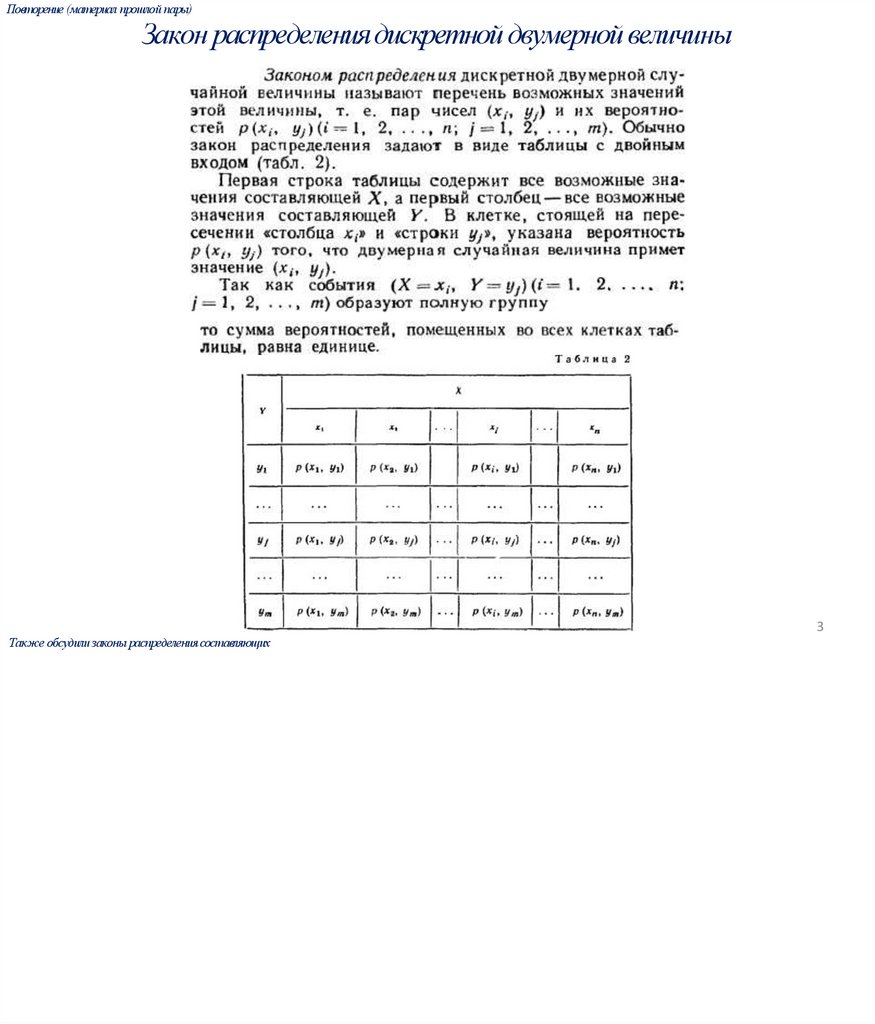
Повторение (материал прошлой пары)
Закон распределения дискретной двумерной величины
3
Также обсудили законы распределения составляющих

3.

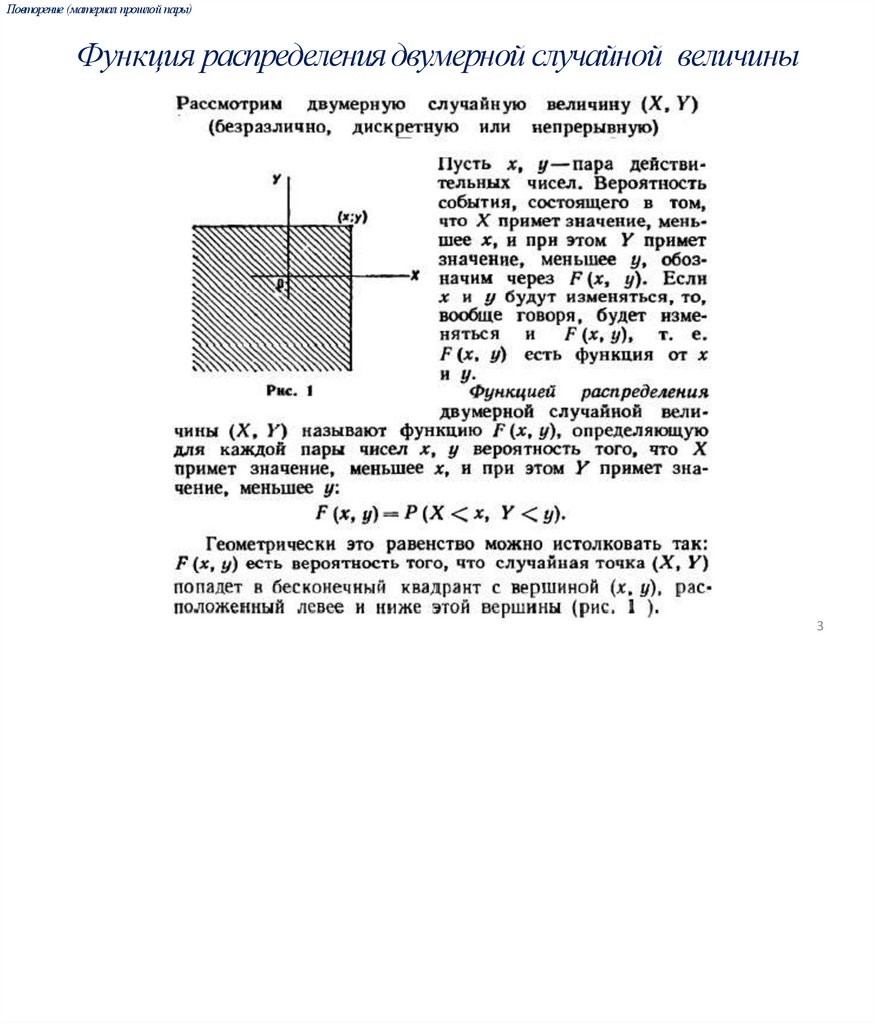
Повторение (материал прошлой пары)
Функция распределения двумерной случайной величины
3

4.

Свойства функции распределения двумерной случайной величины
4

5.

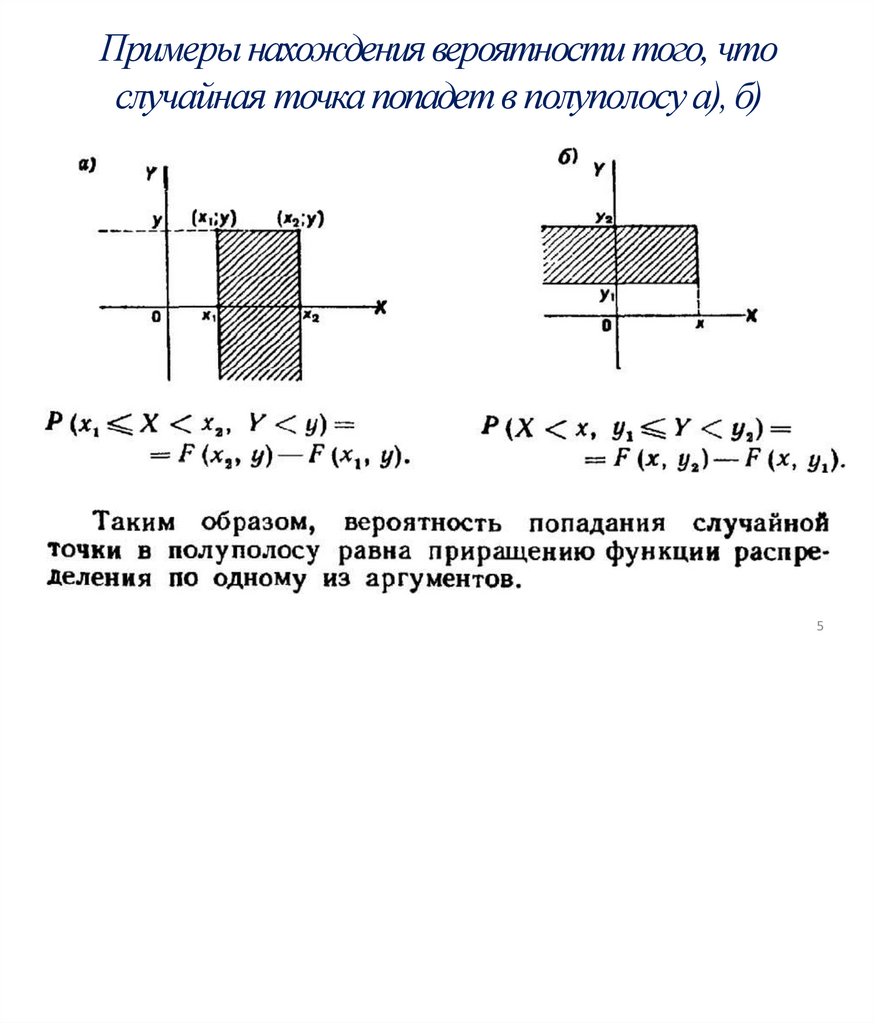
Примеры нахождения вероятности того, что
случайная точка попадет в полуполосу а), б)
5

6.

Пример 1
6

7.

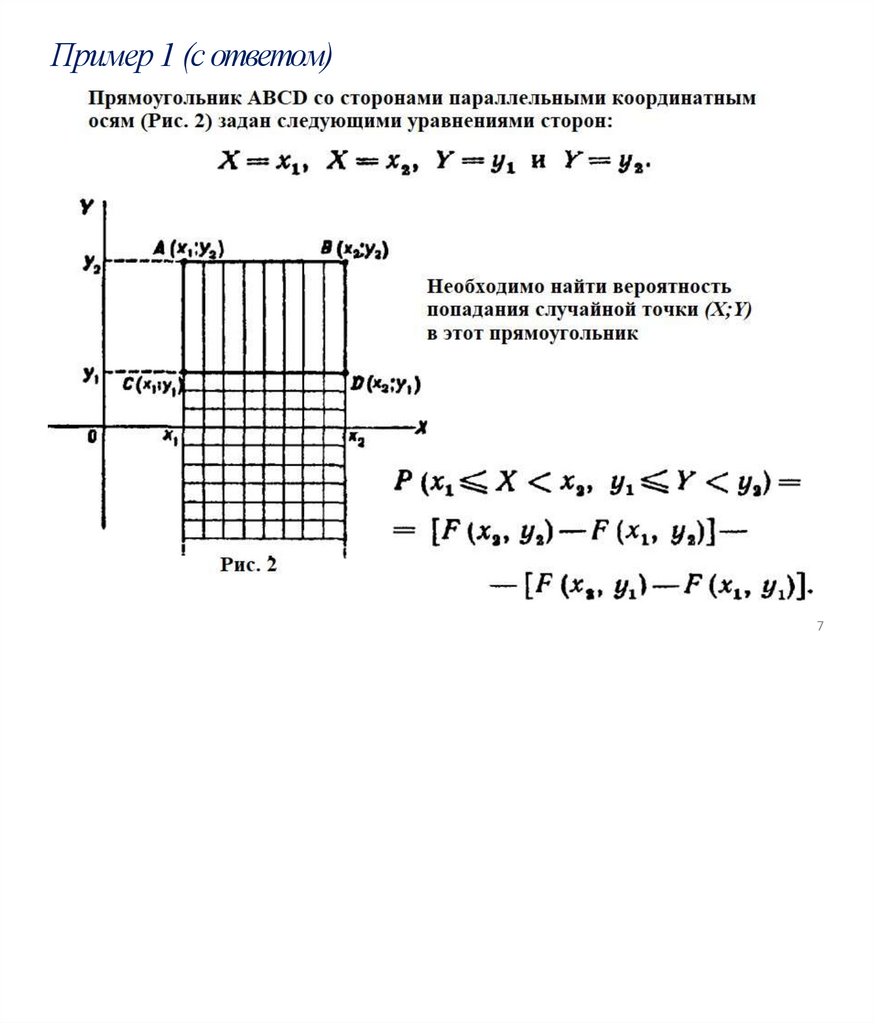
Пример 1 (с ответом)
7

8.

Плотность совместного распределения вероятностей
Непрерывную двумерную величину можно задать не только при помощи функции
распределения, но также и пользуясь плотностью распределения.
Пусть функция F(x,y) всюду непрерывна и имеет непрерывную частную производную
второго порядка (за исключением, быть может, конечного числа кривых)
Плотностью совместного распределения вероятностей f(x,y) двумерной
непрерывной случайной величины (X,Y) называют вторую смешанную частную
производную от функции распределения:
Геометрически эту функцию можно истолковать как поверхность, которую называют
поверхностью распределения (Рис.3)
Зная же плотность совместного распределения f(x,y),
Можно найти функцию распределения F(x,y)
по формуле:
Рис. 3
8

9.

Вероятность попадания точки в область D
Чтобы вычислить вероятность попадания
случайной точки (X;Y) в область D,
необходимо найти двойной интеграл по
области D от функции f(x,y).
То есть вероятность попадания случайной
точки (X;Y) в область D равна объему тела,
ограниченного сверху поверхностью z=f(x,y),
основанием которого служит проекция этой
поверхности на плоскость xOy.
Рис. 4
Рис. 3
9

10.

Плотностираспределения составляющих
Известна плотность совместного распределения вероятностей системы двух
случайных величин. Найдем плотности распределения каждой из оставляющих.
Обозначим за
функцию распределения составляющей X
10

11.

Плотностираспределения составляющих
Т.о. плотность распределения одной из составляющих равна несобственному
интегралу с бесконечными пределами от плотности совместного распределения
системы, причем переменная интегрирования соответствует другой составляющей
Пример:
11

12.

Условное распределение
12

13.

Пример 2
14

14.

Условная плотность
(1)
Примечание: в отличие от безусловной плотности
условная плотность
Дает распределение X при условии, что составляющая Y приняла значение Y = yi;
функция же
дает распределение X независимо от того, какие из возможных
значений приняла составляющая Y.
(2)
(3)
(4)
Таким образом, умножая закон распределения одной из составляющих на условный
закон распределения другой составляющей, находим
15
закон распределения системы случайных величин.

15.

Пример 3
(3)
(4)
15

16.

Условное математическое ожидание
16

17.

Пример 4.
17

18.

Необходимые и достаточные условия независимости
случайные величины
18

19.

Числовые характеристики системы двух случайных величин
Корреляционный момент
19

20.

… о единицах измерения корреляционного момента
… о трудностях при сравнении корреляционных моментов различных систем сл.величин.
20

21.

Коэффициент корреляции
Значения
коэффицие
нта
Интерп
ретация
от 0 до 0,3
очень
слабая
от 0,3 до 0,5
слабая
от 0, 5 до 0,7 средняя
от 0,7 до 0, 9
высокая
от 0,9 до 1
очень
высокая
Таблица анализа силы связи
между переменными
… коррелированные и некоррелированные случайные величины …
21

22.

23.

24.

25.

Линейная регрессия