Математический анализ. Лекция №7. Предел функции. Непрерывные функции

1.

Математический анализ
ЛЕКЦИЯ № 7
Предел функции. Непрерывные
функции.

2.

§ 1. Определение предела функции
1. 1 Определение предела функции
Пусть функция y f (x) определена в некоторой окрестности точки a ,
кроме, быть может, самой точки a .
Определения.
1. (на языке ). Число A называется п р е д е л о м ф у н к ц и и
f (x) в т о ч к е a , если для любого положительного найдется такое
положительное число , что для всех x a , удовлетворяющих неравенству
x a , выполняется неравенство:
f ( x) A .
В этом случае пишут:
lim f ( x) A .
x a
Это определение можно записать в виде:
( 0 0 x : x a , x a f ( x) A )
lim f ( x) A .
x a

3.

2. (на языке последовательностей). Число A называется пределом
функции f (x) в т. a , (или при x a ), если для любой сходящейся к a
последовательности xn значений аргумента
x , отличных от a ,
соответствующая последовательность f xn значений функции сходится к
числу A .
Предел функции в точке a обозначается:
lim f ( x) A или f ( x) A при x a .
x a
Определение 2 дает понятие предела функции через предел последовательности,
ранее нами освоенный. Определения 1 и 2 эквивалентны. В частности из
определения 1 следует, что lim f x A , если при «сгущении» точек x около т. a
x a
соответствующие значения y «сгущаются» около значения y A .
3. Под окрестностью бесконечно удаленной точки будем понимать множество
точек x , таких, что x A M M : 0 M .

4.

4. Число A называется пределом f x при x , если 0 M 0 такое, что
f x A
x : x M . Обозначение: lim f ( x) A .
x
В дальнейшем a считаем как конечным так и бесконечным.
5. Будем говорить, что f x при x a , если M 0 M 0 такое,
что из x a f x M . Обозначение: lim f ( x) .
6. Левосторонним
lim f x f a 0
x a 0
x a
[правосторонним
lim f x f a 0 ]
x a 0
пределом f x при x a называется предел f x при x a , причем x ,
стремясь к a , остается все время меньше (больше) a .
Очевидно, что если f a 0 f a 0 C lim f ( x) C.
x a

5.

1.1.1 Свойства пределов
1. Пусть lim f1 x lim f 2 x A , lim x B и в некоторой окрестности т. a
x a
x a
x a
а) f1 x x , x a . Тогда A B .
б) f1 x x f 2 x , x a . Тогда lim x A .
x a
2. Предел постоянной равен самой постоянной.
3. Если существуют конечные пределы lim f x и lim x , то:
а) lim f x x lim f x lim x ,
x a
x a
x a
x a
x a
x a
x a
б) lim f x x lim f x lim x
x a
в) если С const , то lim C f x C lim f x ,
x a
x a
f x
f x lim
x a
г) lim
, если lim x 0 .
x a x
x a
lim x
x a
З а м е ч а н и е 1. Очевидно, что приведенные свойства для функции, верны
и для последовательностей, как верно и обратное.

6.

§ 2 Бесконечно малые и бесконечно большие величины
Определение 7. Функция x называется бесконечно малой (большой)
x 0 lim x .
при x a , если lim
x a
x a
Пусть u a - некоторая окрестность т. a , x - бесконечная малая, a x
- бесконечно большая при x a .
Теоремы.
f x b , необходимо и достаточно, чтобы
1. Для того, что бы lim
x a
f x b x x u a .
2. Если в u a : f x ограничена, (x) - бесконечно малая, x - бесконечно
большая то
f x
f x
lim
,
lim
0.
x a x
x a x
3. Если в u a : f x ограничена и (x) - бесконечно малая, то
lim f x x 0
x a
Пусть x и x - бесконечно малые при x a , и существует предел
x
lim
С.
x a x
Тогда, если а) С 0 - конечное, то и - бесконечно малые одного порядка, a
если C 1, то и - эквивалентные ~ .

7.

З а м е ч а н и е 1.
а) В процессе нахождения предела, любую величину можно заменить
эквивалентной ей величиной.
б) При C 0 - бесконечно малая более высокого порядка, чем . Этот факт
записывается в виде 0 .
в) При C - бесконечно малая более высокого порядка, чем .
Составим таблицу эквивалентных бесконечно малых функций, которую
можно использовать при вычислении пределов. При ( x ) 0
1) sin ( x ) ~ (x )
6) e
2) tg (x ) ~ (x )
7) a
3) arcsin ( x ) ~ (x )
8) ln( 1 ( x )) ~ (x )
4) arctg (x ) ~ (x )
9) log a (1 ( x)) ~ ( x) log a e
5) 1 cos ( x ) ~
11)
2 ( x)
1 ( x) 1 ~
2
(x)
2
10)
( x)
1 ~ (x )
( x)
1 ~ ( x) ln a
n
1 ( x) 1 ~
( x)
n

8.

2.1 Неопределенности
f x
C , если он существует.
x a x
1. B 0 - конечное. В этом случае, вне зависимости от вида функций f x и
f x A , lim x B . Найдем lim
Пусть lim
x a
x a
x , C
A
.
B
2. A B 0 , C ?
В случае A B 0 значение C , без знания конкретного вида функций
f x и x неопределено, и поэтому говорят, предел отношения
является неопределенностью вида
0
.
0
Приведем основные неопределенности:
0
,
0
, 0 , , 1 , 0 , 0 .
f x
при x a
x

9.

§ 3. Замечательные пределы
Пусть x - некоторая функция, причем
lim x 0
(1)
x a
0
Определение 8. Первым замечательным пределом при неопределенности и
0
называется предел, вида:
sin x
1
x a
x
(2)
lim
Определение 9. Вторым замечательным пределом с неопределенностью 1
называется предел, вида:
1
(3)
lim 1 x x e
x a
Замечание. Имеет место формула
lim f ( x)
x
x x0
Последовательность
можно
1 e
lim x f ( x) 1
x x 0
рассматривать
.
как
функцию
натурального
аргумента, т.е. y xn f (n).
Последовательность, имеющая предел, называется сходящейся, в противном
случае – расходящейся.

10.

§ 4. Непрерывные функции
Пусть в Rn в некоторой окрестности т. M 0 определена функция
y f (M ) .
Определение 10. Функция f M называется непрерывной в т. M 0 , если
а) f M определена в т. M 0 ,
б) существует предел lim f M ,
в) lim f M f M 0 .
M 0
M M 0
Если нарушено хотя бы из условий а), б), в), то M 0 называют точкой
разрыва функции y f M . Из в) следует, что под знаком непрерывной
функции можно переходить к пределу, т.е. lim f ( x) f lim x .
x x0
x x0
Рассмотрим свойства непрерывных функций для функция одной
переменной y f (x).
Определение 11. Если f x непрерывна в т. a , то f a 0 f a 0 f a .

11.

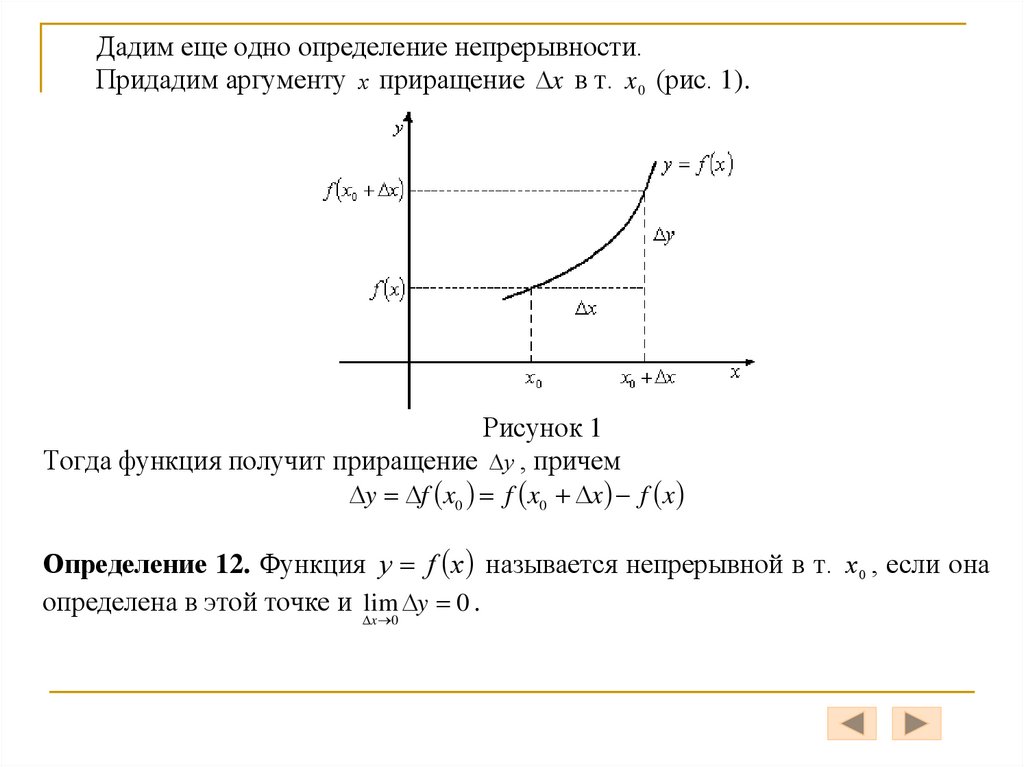
Дадим еще одно определение непрерывности.
Придадим аргументу x приращение x в т. x 0 (рис. 1).
Рисунок 1
Тогда функция получит приращение y , причем
y f x0 f x0 x f x
Определение 12. Функция y f x называется непрерывной в т. x 0 , если она
y 0 .
определена в этой точке и lim
x 0

12.

4.1 Классификация точек разрыва
Определение 13. Точка x 0 - точка разрыва f x называется устранимой, если
существует lim f x , но f x не определена в т. x 0 либо lim f x f x0 .
x x0
x x0
Рисунок 2
Если f x 0 не определена, а lim f x A , положив f x0 A , можно сделать
x a
f x непрерывной в т. x 0 (рис. 2).
Определение 14. Точка x0 называется точкой разрыва первого рода, если
существуют конечные f x0 0 , f x0 0 , причем f x0 0 f x0 0 .

13.

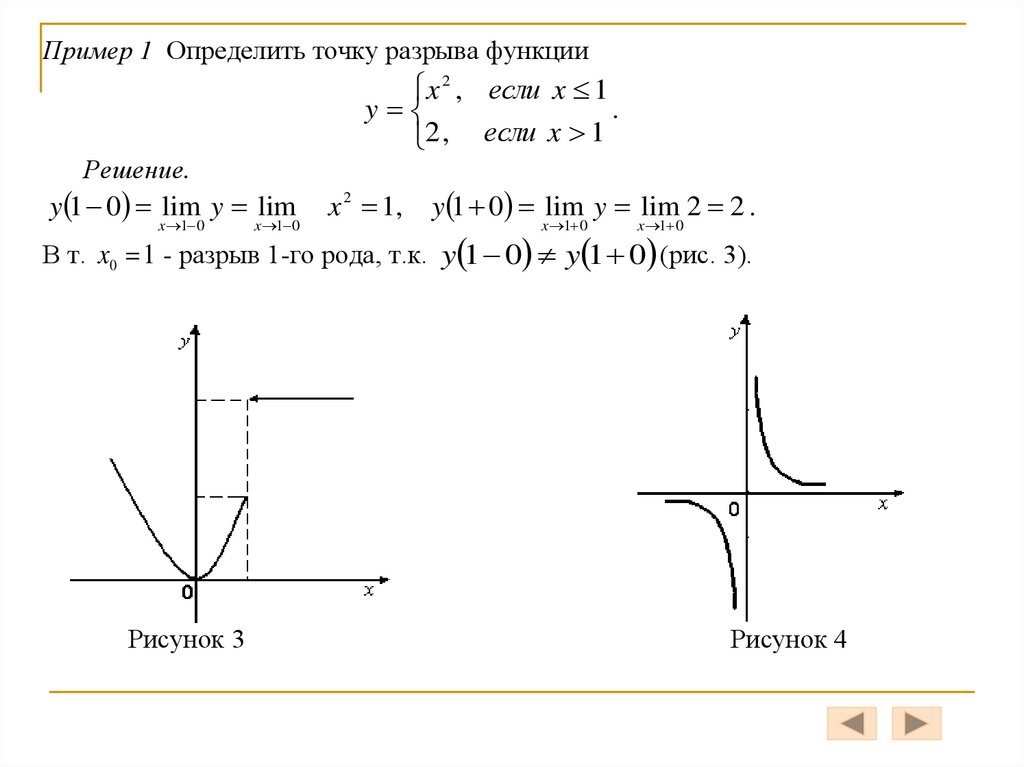
Пример 1 Определить точку разрыва функции
x 2 , если x 1
.
y
2 , если x 1
Решение.
y 1 0 lim y lim
x 1 0
x 1 0
x 2 1,
y 1 0 lim y lim 2 2 .
x 1 0
x 1 0
В т. x0 1 - разрыв 1-го рода, т.к. y 1 0 y 1 0 (рис. 3).
Рисунок 3
Рисунок 4

14.

Определение 15. Если у функции не существует правого или левого
предела, или же эти пределы бесконечны, то говорят, что она имеет
разрыв второго рода в этой точке.
1
Пример 2. y , x0 0 (рис. 4).
x
Решение.
lim
y , lim
y . Следовательно, т.0 – точка разрыва 2-ого
x 0
x 0
рода.

15.

4.2 Функции, непрерывные на отрезке
Определение 16. Функция f x называется непрерывной на отрезке a; b ,
если она непрерывна в каждой точке a; b и f a 0 f a , f b 0 f b .
Класс непрерывных в области D функций обозначается C D .
Теоремы.
1. Если f x C a ; b , то f x ограничена на a; b .
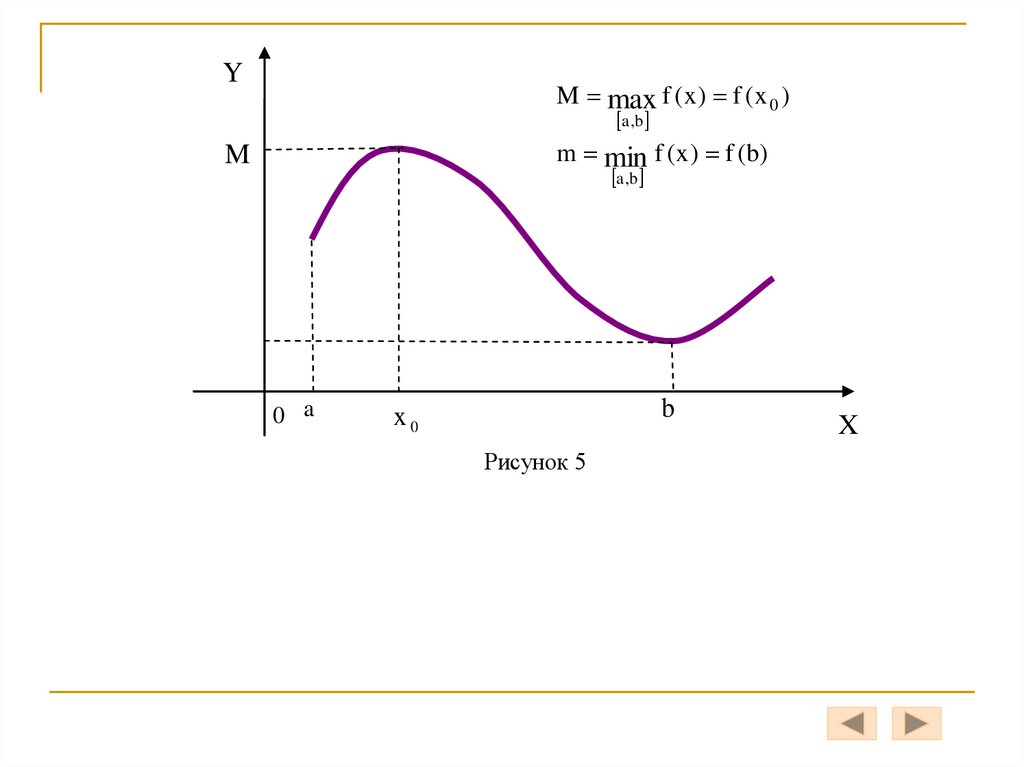
2. Если f x C a ; b , то f x достигает на этом отрезке хотя бы один раз
наибольшего значения M и наименьшего значения m , т.е.
m f x M x a ; b (рис. 5)

16.

Y
M max f ( x ) f ( x 0 )
a ,b
m min f ( x ) f (b)
M
a ,b
0 a
b
x0
Рисунок 5
X

17.

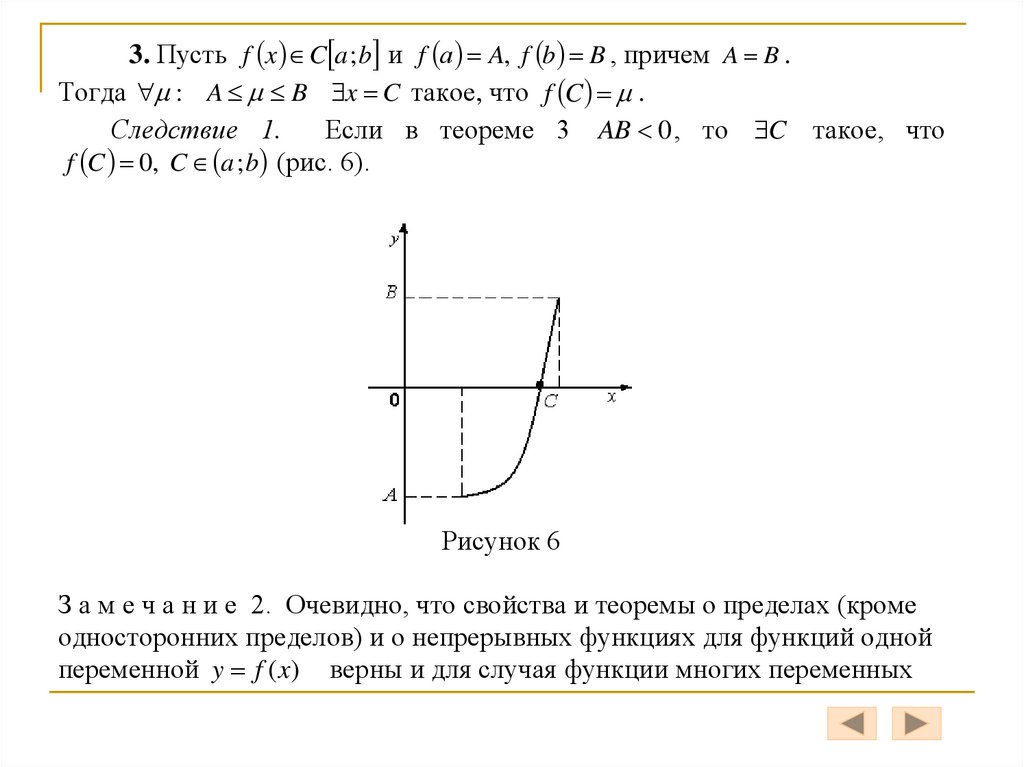
3. Пусть f x C a ; b и f а A, f b B , причем A B .
Тогда : A B x C такое, что f C .
Следствие 1.
Если в теореме 3 AB 0 , то C такое, что
f C 0, C a ; b (рис. 6).
Рисунок 6
З а м е ч а н и е 2. Очевидно, что свойства и теоремы о пределах (кроме
односторонних пределов) и о непрерывных функциях для функций одной
переменной y f (x) верны и для случая функции многих переменных