Схема (формула) Бернулли. Формула Пуассона. Локальная и интегральная теоремы Муавра-Лапласа

1.

ЛЕКЦИЯ №4. Схема (формула) Бернулли.
Формула Пуассона. Локальная и интегральная
теоремы Муавра-Лапласа
С понятием «независимых
«независимых испытаний».
событий»
связано
понятие
Определение. Испытания называются независимыми, если они
повторяются многократно, а вероятность наступления некоторого
события А в каждом испытании не зависит от исходов других
испытаний.
Примеры независимых испытаний: подбрасывание монеты n раз,
стрельба по мишени (n раз) без поправок на допущенную ошибку
при новом выстреле, пр.
1

2.

Формула Бернулли
Пусть производится n независимых испытаний, в каждом из
которых вероятность появления события А (его называют успехом)
равна p, а вероятность появления ему противоположного события
(его называют неудачей) равна q=1-p. Такая последовательность
опытов называется схемой Бернулли.
Например, при стрельбе по мишени
Событие А={попадание в мишень}
Событие A
непопадание в мишень
2

3.

Пусть требуется определить вероятность того, что событие А
произойдет ровно k раз в серии из n испытаний.
Теорема. Если производится n независимых испытаний, в
каждом из которых вероятность появления события А равна p, а
вероясть его непоявления равна q=1-p, то вероятность того, что
событие А произойдет ровно k раз в серии из n испытаний
определяется формулой Бернулли
P (k ) = Ck pk qn k
,
n
10
Событие наступит:
P n (k
менее k раз Pn (0) Pn (1) Pn (2)
1)
более k раз
Pn (k 1) Pn (k 2)
P n ( n)
не менее k раз
Pn (k ) Pn (k 1) Pn (k 2)
не более k раз P n P 0
Pn (1) Pn (2)
n( )
n( )
P n (k )
3

4.

Задача. Производится 3 независимых выстрела по цели.
Вероятность попадания в цель при каждом выстреле одинакова и
равна p=0,9. Какова вероятность: 1) промаха; 2) одного попадания;
3) двух попаданий; 4) трёх попаданий? Решить задачу в случае,
если вероятности попадания при разных выстрелах различны:
p1=0,7; p2=0,8; p3=0,9.
Решение. По формуле Бернулли
P3 (0 ) = C (0,9 ) (0,1) = 0,001
Вероятность промаха
P3 (1) = C (0,9 ) (0,1) = 0,027
Вероятность одного попадания
0
0
3
1
3
1
3
2
P3 (2 ) = C (0,9 ) (0,1) = 0, 243 Вероятность двух попаданий
2
3
2
1
P3 (3) = C (0,9 ) (0,1) = 0,729
3
3
3
0
Вероятность трёх попаданий
4

5.

Решим задачу в предположении, что вероятности попадания в
цель при каждом выстреле различны.
Рассмотрим события:
А={цель поражена один раз}.
А1={цель поражена при первом выстреле}
A2={цель поражена при втором выстреле}
A3={цель поражена при третьем выстреле}
События А1, А2, А3 независимы и несовместны. Тогда
A = A1 A2
A3 + A1 A2
A3 + A1 A2
A3
P (A ) = P (A1 ) P (A2 ) P (A3 )+ P (A1 ) P (A2 ) P (A3 )+
+P (A1 ) P (A2 ) P (A3 ) = 0,7 0,2 0,1 + 0,3 0,8 0,1+
+0,3 0,2 0,9 = 0,014 + 0,024 + 0,054 = 0,092
5

6.

Рассмотрим событие В={цель поражена два раза}. Тогда
событие В состоит в следующем:
B = A1 A2
A3 + A1 A2
A3 + A1 A2
A3
Вероятность события В вычисляется как
P (B )= P (A1 ) P (A2 ) P (A3 )+ P (A1 ) P (A2 ) P (A3 )
+
+ P (A1 ) P (A2 ) P (A3 ) = 0,7 0,8 0,1 + 0,3 0,8
0,9 +
+ 0,7 0,2 0,9 = 0,056 + 0, 216 + 0,126 = 0,398
6

7.

Рассмотрим событие C={цель поражена три раза}. Тогда
событие С состоит в следующем:
C = A1 A2
A3
Вероятность события С вычисляется как
P (C ) = P (A1 ) P (A2 ) P (A3 ) = 0,7 0,8 0,9 = 0,504
Рассмотрим событие D={по цели допущен промах}. Тогда
событие D состоит в следующем:
D = A1 A2
A3
Вероятность события С вычисляется как
P (D )= P (A1 ) P (A2 ) P (A3 )= 0,3 0,2 0,1 = 0,006
7

8.

Предельные теоремы в схеме Бернулли
При большом значении числа испытаний или малой
вероятности наступления события использование формулы
Бернулли практически невозможно. В этом случае используют
предельные теоремы, содержащие приближенные формулы со сколь
угодной малой относительной погрешностью.
К таким теоремам относятся:
Теорема Пуассона;
Локальная теорема Муавра-Лапласа;
Интегральная теорема Муавра-Лапласа.
8

9.

Теорема 1 (Пуассона). Если число испытаний неограниченно
увеличивается и вероятность наступления события в каждом
испытании неограниченно уменьшается, но так, что их
произведение является постоянной величиной, то вероятность Pn(k)
может быть вычислена по приближённой формуле Пуассона
Pn (k )
k
e
, n 50,
k!
= np 10
λ - параметр Пуассона
Формула Пуассона применяется, когда число испытаний велико,
а вероятность наступления события (например, выигрыш
автомобиля по лотерейному билету) крайне мала.
Формула Пуассона
обслуживания.
используется
в
теории
массового
9

10.

Задача. Завод «Золотая балка» отправил в Москву 1500 бутылок
вина «Каберне». Вероятность того, что в пути бутылка может
разбиться, равна 0,002. Найти вероятность того, то в пути будет
разбито не более 2-х бутылок.
Решение. Рассмотрим событие А={в пути будет разбито не
более 2-х бутылок}. Здесь
n = 1500 > 50;
p = 0,002;
= 1500 0,002 = 3 < 10
P (A) = P1500 (0 )+ P1500 (1)+ P1500 (2 ) =
0
1
2
3
3
3
= e 3 + e 3 + e3
0!
1!
2!
0,423
10

11.

Теорема 2 (локальная теорема Муавра-Лапласа). Если
вероятность наступления события А в каждом испытании постоянна
и отлична от нуля и единицы, а число независимых испытаний
достаточно велико, то вероятность Pn(k) может быть вычислена по
приближённой формуле
Pn (k )
1
· (x ),
npq
(x) =
–
x2
1
e 2,
2
x=
k
np
npq
n > 10, np > 10
Свойства функции φ(x):
( x )= (x )
x 4 (x ) = 0
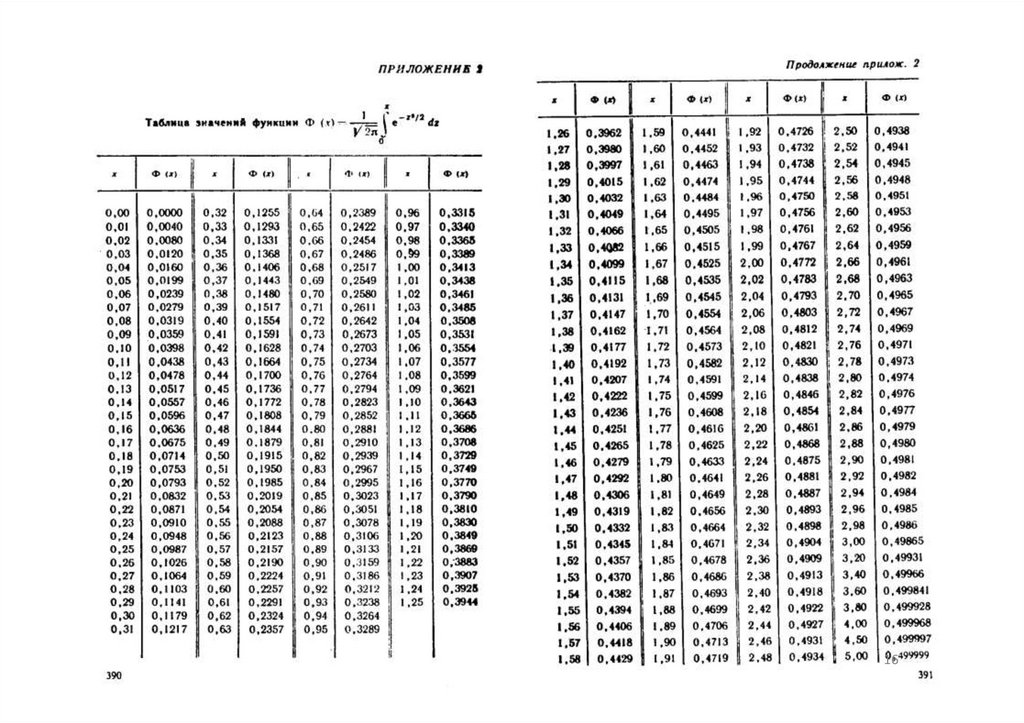
Значения функции φ(x) протабулированы на интервале (0;4) с
шагом 0,01 и помещены в Приложение 1 сборника задач по теории
вероятностей и математической статистике.
11

12.

12

13.

Задача. Вероятность попадания в мишень при одном выстреле
равна 0,7. Найти вероятность того, что при 200 выстрелах мишень
будет поражена 160 раз.
Решение. Здесь
n = 200 > 10; k = 160;
p = 0,7; q = 1
p = 0,3;
npq = 200 0,7 0,3 = 42 6,48
x=
160
200 0,7
20
=
3,09;
6,48
42
P200 (160 )
(3,09 ) 0,0034
1
·0,0034 0,0005
6,48
13

14.

В тех случаях, когда требуется вычислить вероятность того, что
в n независимых испытаниях событие А появится не менее k1 раз, но
не более k2 раз, используют интегральную теорему МуавраЛапласа.
Теорема 3 (интегральная теорема Муавра-Лапласа). Если
вероятность наступления события А в каждом испытании постоянна
и отлична от нуля и единицы, то вероятность P(k1;k2) может быть
найдена по приближённой формуле
P (k1 ;k2 )
x2 =
,
k2
np
npq
x1 =
,
(x2 )
k1
np
npq
(x1 ),
np > 10
14

15.

Свойства функции Лапласа:
( x )=
x 5
(x )
(x ) = 0,5
Значения интегральной функции Лапласа протабулированы на
интервале (0;5) с шагом 0,01 и помещены в Приложение 2 сборника
задач по теории вероятностей и математической статистике.
15

16.

16

17.

Задача. Имеется 100 станков, каждый из которых оказывается
включенным с вероятностью 0,8 в течение всего рабочего времени.
Найти вероятность того, что в произвольный момент времени
работают от 70 до 86 станков.
Решение. Здесь
n = 100;
p = 0,8; q = 1
P (70;86 )
(x2 )
86 80
x2 =
=1,5;
100 0,8 0,2
2
P (70;86)
(1,5)
0,8 = 0, 2; k1 = 70; k2 = 86
(x1 ),
70 80
x1 =
= 2,5
100 0,8 0,
( 2,5) = 0,4332 + 0,4938 = 0,9270
17

18.

Случайные величины
Определение. Случайной величиной называется величина,
которая в результате опыта принимает то или иное значение,
заранее неизвестно, какое именно.
Обозначение
X ,Y , Z ,
,,
Случайные величины делятся на два типа: дискретные и
непрерывные.
18

19.

Определение. Случайная величина Х называется дискретной,
если она принимает конкретное определенное значение.
X : (x1 , x2 , xn )
Кроме значений, для полного описания дискретной случайной
величины необходимо знать вероятности этих значений.
pi = P (X = xi ), i = 1,2, ,n
19

20.

Определение. Любое правило (таблица, функция, график),
указывающее возможные значения дискретной случайной
величины и соответствующие им вероятности, называется рядом
распределения дискретной случайной величины.
Ряд распределения удобно отображать в виде таблицы
X:
i = 1, n
xi
x1
x2
…
xn
pi
p1
p2
…
pn
pi 0;
p1 + p2 + + pn =
n
pi = 1
i=1
20

21.

Пусть дан ряд распределения дискретной случайной величины Х
X:
xi
x1
x2
…
xn
pi
p1
p2
…
pn
Если в системе координат
Oxp построить точки с
координатами (xi, pi) и
соединить их ломаной
линией, то полученная кривая
называется многоугольником
распределения.
21

22.

Определение. Случайная величина X называется непрерывной,
если все ее возможные значения сплошь занимают некоторый
промежуток.
Примеры непрерывных случайных величин: время ожидания
пассажиром транспорта, рост человека, ошибки стрельбы, уровень
шума в радиоприёмнике и т.д.
22

23.

Универсальным способом задания закона распределения
вероятностей для дискретных и непрерывных случайных величин
является функция распределения.
Определение. Функцией распределения случайной величины X
называется функция F(x), которая для любого действительного
числа x равна вероятности события (X < x)
F (x ) = P (X < x )
F(x) – интегральная функция распределения.
Геометрически: X попадёт в интервал (– ∞; x).
23

24.

Свойства функции распределения
1. 0 F (x ) 1
2. F (x )неубывающая
3. F (
4.
) = P (X < ) = 0; F (+ )= P (X < + )= 1
P (a < X < b ) = F (b ) F (a)
Для дискретной случайной величины функция распределения
имеет вид:
F (x ) = P (X < xi )
i
24

25.

Задача. Дан ряд распределения дискретной случайной
величины. Записать функцию распределения и построить ее график.
X:
xi
1
4
5
7
pi
0,4
0,1
0,3
0,2
x <1
F (x )= P (X < 1) = 0
1 x<4
F (x ) = P (X < 4 ) = P (X = 1)= 0, 4
4 x<5
F (x ) = P (X < 5 )= P (X = 1)+ P (X = 4 ) = 0, 4 + 0,1 = 0,5
5 x<7
F (x ) = P (X < 7 )= P (X = 1)+ P (X = 4 )+ P (X = 5 ) = 0,8
x 7
F (x ) = 1
25

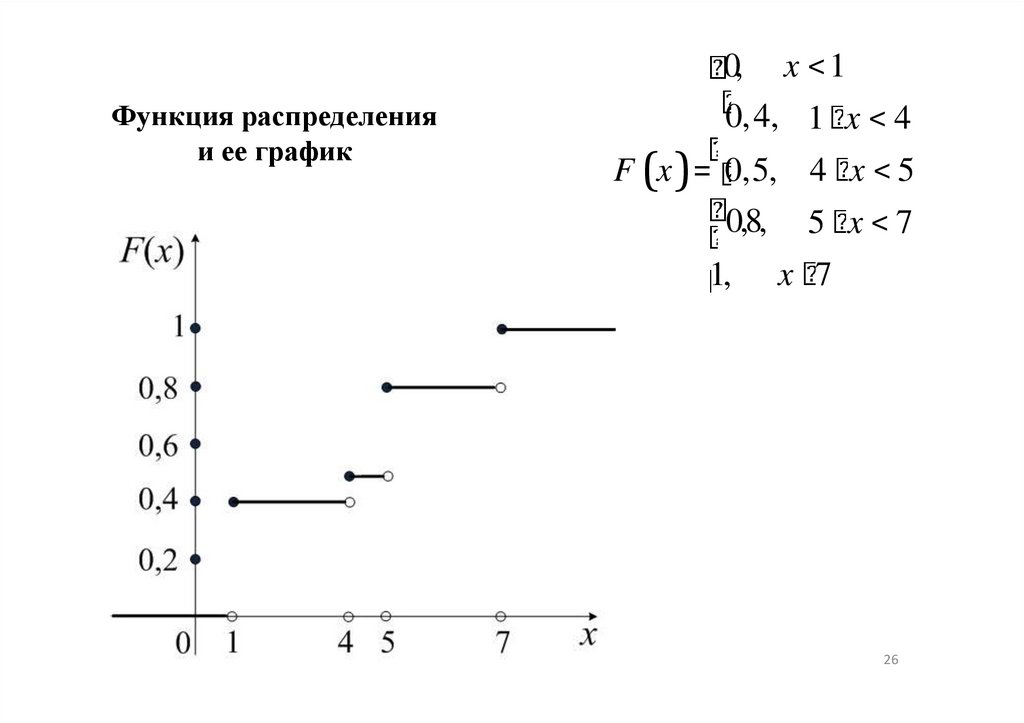
26.

Функция распределения
и ее график
0, x < 1
0,4, 1 x < 4
F (x ) = 0,5, 4 x < 5
0,8,
1,
5 x<7
x 7
26

27.

Задача. Дана функция распределения.
F (x) =
0,
x
2
1,
x 0
, 0< x 2
x>2
Найти вероятность того, что случайная величина X примет значение
из интервала [1; 3).
P (1 X < 3)= F (3)
1 1
x
=
1
=
F (1) = 1
2 2
2 x=1
27