Similar presentations:
Дифференцирование функций комплексной переменной
1.
ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙПроизводная функции комплексного переменного в точке вводится так же,
как и в действительной области. Пусть f z определена и однозначна в некоторой окрестности точки z0 . Если существует конечный предел отношения
f z0 z f z0
при z 0 ,
z
то этот предел называется производной функции f z в точке z0 и обозначается f z0 , а сама функция f z называется дифференцируемой в точке z0 .
Функция, дифференцируемая в каждой точке области, называется дифференцируемой в области.
Теорема. Функция f z дифференцируема в точке z0 тогда и только
тогда, когда приращение f f z0 z f z0 может быть представлено
в виде f A z o z , где A – комплексная постоянная, не зависящая от z .
Для дифференцируемой функции f z0 A .
Следствие. Если f z дифференцируема в точке z0 , то она непрерывна
в этой точке.
1
2.
Правила дифференцированияТак как производная функции комплексного переменного определя f z
ется, как и в действительной области, т.е. в виде предела lim
, то,
0
z
используя это определение и свойства пределов, несложно убедиться
в справедливости правил дифференцирования, известных из математического анализа.
1. Если f z и g z дифференцируемы в точке z0 , то
f g f g ; cf cf ; fg f g g f ;
f f g g f
если g z0 0 , то
.
2
g
g
2. Если f z дифференцируема в точке z0 , а F дифференциру-
ема в точке 0 f z0 , то функция z F f z дифференцируема
в точке z0 , причем z0 F 0 f z0 .
2
3.
« f z u x, y iv x, y непрерывна в точке z x iy »«функции u x, y и v x, y непрерывны в точке x, y »
Для дифференцируемости аналогичное утверждение не выполняется.
Условие Коши-Римана
Для того чтобы f z u x, y iv x, y была дифференцируема в точке
z x iy необходимо и достаточно, чтобы
1) функции u x, y и v x, y были дифференцируемы в точке x, y ,
2) в точке x, y выполнялось условие Коши-Римана:
u v u
v
.
,
x
x y y
Производную дифференцируемой функции можно вычислить по любой
из приведенных ниже формул:
u v v u u u v v
f z
i
i
i
i .
x
x y
y x
y y x
3
4.
Условие Коши-Римана в полярных координатахДля того чтобы функция f z u r , iv r , была дифференцируема в точке z rei необходимо и достаточно, чтобы
1) функции u r , и v r , были дифференцируемы в точке r , ,
2) в точке r , выполнялось условие Коши-Римана:
u 1 v v
1 u
,
.
r r r
r
Производную дифференцируемой функции
по любой из приведенных ниже формул:
можно
вычислить
r u v 1 v
u 1 u u 1 v
v
f z i
i r i
ri .
z r
r z z r
z
r
5
5.
z x iy ,Примеры
1. f z az b , a, b
f z u x, y iv x, y
дифференцируема всюду и f z a .
Пусть a ax ia y , b bx iby , где ax , a y , bx , by , тогда
f z a x ia y x iy bx iby ,
u x, y ax x ya y bx ,
v x, y a y x yax by .
u
v
u
v u
v
и f z
i ax ia y a .
ax ,
a y
x
x
x
y y
x
df
2. f z e e x cos y i sin y дифференцируема всюду и f z e z .
z
u x, y e x cos y , v x, y e x sin y
u
v
u
v u
v
i e z .
,
и f z
e x cos y
e x sin y
x
x
x
y y
x
7
6.
3. f z z n , nдифференцируема всюду и f z nz n 1 .
Пусть z rei , тогда f z r nei n , т.е.
u z u r , r n cos n , v z v r , r n sin n .
Следовательно,
u
1 v v
1 u
n 1
n 1
nr cos n
nr sin n
,
.
r
r r
r
r u v r
f z i nr n 1 cos n i nr n 1 sin n
z r
r z
r n r n 1ei n
rei
nr
n 1 i n 1
e
nz n 1 .
8
7.
Аналитические функцииВ теории и практике применения функций комплексного переменного
интерес представляют дифференцируемые функции, причем имеющие производные не в отдельных точках, а на множествах — в областях.
Функция w f z называется:
– аналитической в точке z , если она дифференцируема как в самой
точке z , так и в некоторой ее окрестности;
– аналитической в области D , если она дифференцируема в каждой
точке этой области;
– аналитической на замкнутом множестве D , если она является аналитической в некоторой области B , содержащей это множество D B .
Точки, в которых функция не является аналитической, называются её
особыми точками.
Теорема. Если функция w f z непрерывна в области D
и z D
выполняются условия Коши-Римана, то f z является аналитической в D .
9
8.
Свойства аналитических функций1. Сумма, разность и произведение функций, аналитических в точке, есть
функция, аналитическая в этой точке.
2. Частное функций, аналитических в точке, есть функция, аналитическая
в этой точке, если знаменатель в ней отличен от нуля.
3. Суперпозиция аналитических функций — функция аналитическая.
4. Если f z — аналитическая в точке z0 и f z0 0 , то обратная
функция z f 1 является аналитической в точке 0 ( 0 f z0 ).
Теорема. Функция, аналитическая в точке, имеет в этой точке производные любого порядка.
Доказательство теоремы будет позже.
Теорема. Если f z u x, y iv x, y аналитическая функция, то в плоскости xy семейства кривых u x, y C и v x, y C взаимно ортогональны.
u x v y , u y v x grad u grad v u x , u y v x , v y 0 .
10
9.
Связь аналитических функций с гармоническимиФункция f x, y называется гармонической в области D
,
2 f 2 f
если z D f 2 2 0 .
x
y
Гармонические функции u x, y и v x, y , связанные между
собой условиями Коши-Римана, называются сопряженными гармоническими функциями.
Теорема. Действительная и мнимая части любой аналитической в области D функции являются в D сопряженными гармоническими функциями
11
10.
Восстановление аналитической функциипо действительной или мнимой части
Теорема. Для всякой функции
u x, y , гармонической в односвязной
области D , можно найти сопряженную с ней функцию, которая определяется
с точностью до произвольного постоянного слагаемого по формуле
v x, y
x, y
x0 , y0
u
u
dx dy C , x0 , y0 D , x, y D .
y
x
(*)
Замечания:
1 . Если область D многосвязная, то функция v x, y , определяемая формулой (*),
а также функция f z u x, y iv x, y могут оказаться многозначными.
2 . При нахождении функции u x, y по заданной функции v x, y часто вместо
формулы (*) используют условия Коши-Римана.
3 . Для восстановления аналитической в окрестности z0 функции f z также
можно использовать следующие формулы:
z z0 z z 0
z z0 z z 0
или
f z 2u
,
f
z
f
z
2
iv
,
0
f z0 .
2i
2i
2
2
12
11.
Пример 4. Восстановить мнимую часть v x, y аналитическойфункции f z , если u x, y x 3 3xy 2 4 x 2 4 y 2 5 , f i i 1 .
v x, y
С п о с об 1 .
x, y
x0 , y0
u
u
dx dy C
y
x
x, y
6 xy 8 y dx 3x 2 3 y 2 8 x dy C
0,0
x ,0
x, y
y
x
x, y
P x, y dx Q x, y dy * * P x,0 dx Q x, y dy
0,0
0
0
0,0
x ,0
*
y
0 3x 2 3 y 2 8 x dy C 3x 2 y y 3 8 xy C.
0
f i i 1
v 0,1 3x 2 y y 3 8 xy C x 0 1 C 1 C 0
y 1
v x, y 3x 2 y y 3 8 xy.
13
12.
Пример 4. Восстановить мнимую часть v x, y аналитическойфункции f z , если u x, y x 3 3xy 2 4 x 2 4 y 2 5 , f i i 1.
---------------------------------------------------------------Способ 2.
v
u
6 xy 8 y
x
y
v x, y 6 xy 8 y dx y 3x 2 y 8 yx y .
v
u
3 x 2 y 8 x y 3 x 2 8 x y
3x 2 3 y 2 8 x
y y
x
y 3 y 2 y y 3 C
v x, y 3x 2 y y 3 8xy C.
f i i 1
v 0,1 3x 2 y y 3 8 xy C x 0 1 C 1 C 0
y 1
v x, y 3x 2 y y 3 8 xy.
14
13.
Пример 5. Восстановить аналитическую функцию f z по ее действительной части u x, y x 3 3xy 2 4 x 2 4 y 2 5 и начальному условию f i i 1.С п о с об 1.
В предыдущем примере для этой функции была получена
мнимую часть: v x, y 3x 2 y y 3 8 xy. Так как функции u x, y и v x, y
являются многочленами 3-го порядка, то и функция f z также многочлен 3-го
порядка.
Учитывая, что
z x i y,
z 2 x iy x 2 y 2 i 2 xy ,
2
z 3 x iy x 3 3xy 2 i 3x 2 y y 3
3
преобразуем функции u x, y и v x, y :
u x, y x 3 3xy 2 4 x 2 4 y 2 5 x 3 3xy 2 4 x 2 y 2 5 Re z 3 4 z 2 5 ;
v x, y 3x 2 y y 3 8 xy 3x 2 y y 3 8 xy Im z 3 4 z 2 5 .
15
14.
Пример 5. Восстановить аналитическую функциюf z
по ее действительной части u x, y x 3 3xy 2 4 x 2 4 y 2 5 и начальному условию f i i 1.
----------------------------------------------------------------- С п о с о б 2 .
z z0 z z0
z i z i
f z 2u
,
,
1 i
f z0 2u
2i
2i
2
2
2
2
z i 3 z i z i 2
z
i
z
i
2
3
4
4
5 1 i
2
2 2i
2
2i
z 3 4 z 2 5.
16
15.
* ПЛОСКИЕ ФИЗИЧЕСКИЕ ПОЛЯ И ИХ СВЯЗЬ С АНАЛИТИЧЕСКИМИ ФУНКЦИЯМИПусть в области G
задано плоскопараллельное векторное поле F Fx , Fy , где
Fx Fx x, y , Fy Fy x, y дифференцируемые в G функции. Пусть поле F потенциально и соленоидально, т.е.
Fx Fy
div F
0 (2)
x
y
Из (1) следует, что дифференциальная форма Fx dx Fy dy является полным диффе Fy
F
rot F
x 0 (1)
x
y
ренциалом некоторой функции u u x, y , которую называют потенциалом поля F .
Из (2) следует, что Fy dx Fx dy
является полным дифференциалом некоторой
функции v v x , y , которую называют функцией тока.
Рассмотрим функцию f z u x, y iv x, y . Она является аналитической, так
как Fx
u v
u
v
.
и Fy
x y
y
x
Таким образом, всякому потенциальному и соленодальному плоскопараллельному
полю F соответствует аналитическая функция, полностью определяющая это поле.
Эту функцию называют комплексным потенциалом векторного поля F .
Наоборот, каждой аналитической в области G функции f соответствует плоскопараллельное поле F , для которого f является комплексным потенциалом.
17
16.
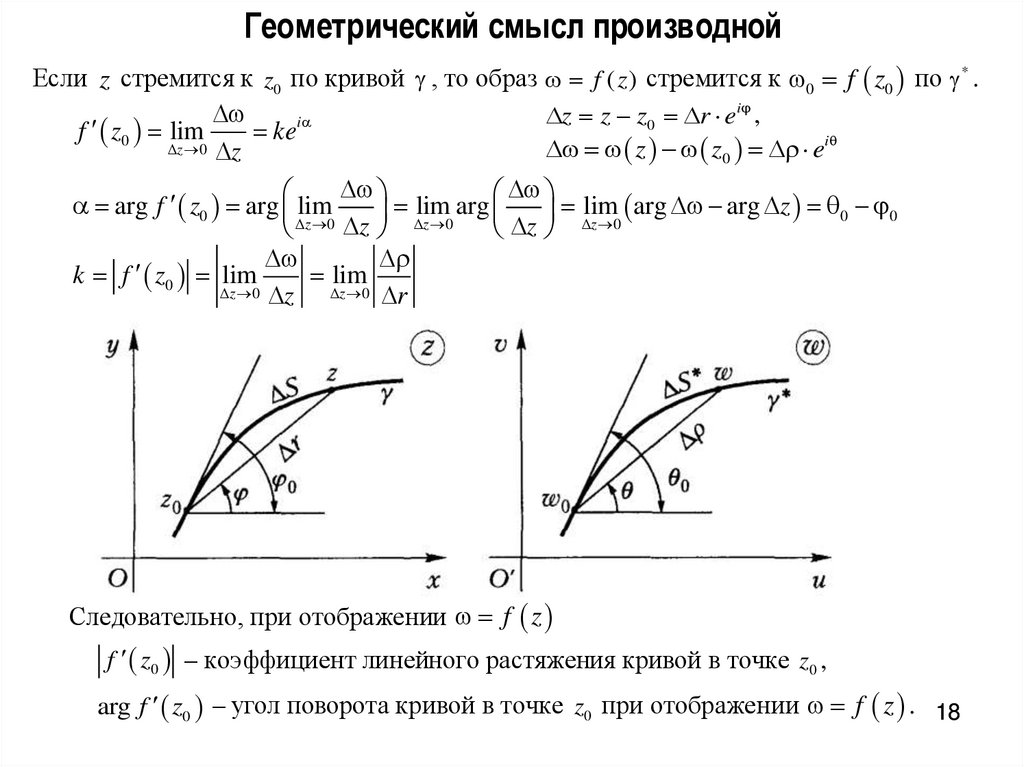
Геометрический смысл производнойЕсли z стремится к z0 по кривой , то образ f ( z ) стремится к 0 f z0 по * .
z z z0 r ei ,
i
f z0 lim
ke
z 0 z
z z0 ei
arg f z0 arg lim
lim
arg
arg arg z 0 0
z 0
lim
z 0 z
z
0
z
k f z0 lim
lim
z 0 z
z 0 r
Следовательно, при отображении f z
f z0 – коэффициент линейного растяжения кривой в точке z0 ,
arg f z0 – угол поворота кривой в точке z0 при отображении f z . 18
17.
Конформные отображенияВзаимно-однозначное отображение области D на область G называется
конформным (от лат. conformus - подобный), если оно сохраняет углы между
кривыми в точках их пересечения.
Если f z – аналитическая в точке z0 функция и f z0 0 , то отображение w f z является конформным в точке z0 .
Если в области D функция
f z однолистна, дифференцируема и
z D f z 0 , то отображение w f z является конформным в D
(т.е. конформным в каждой точке области D ).
При конформном отображении окрестности точки z0 на окрестность точки
w0 бесконечно малые треугольники с вершиной в точке z0 преобразуются в
подобные им бесконечно малые треугольники с вершиной в точке w0 .
19
18.
Геометрический смысл конформных отображенийТеорема (необходимое условие однолистности). Если w f z аналитическая
однолистная в области D функция, то z D f z 0 .
u u x, y ,
w f z u x, y iv x, y
v v x, y .
Из свойств отображений, изучаемых в действительном анализе известно, что условием его взаимно-однозначности в области D является ненулевой якобиан. Для аналитической функции если f z 0 , то J x, y 0 :
J
u x
u y
v x
v y
u x v y v x u y u x v x f z .
2
u x
2
2
v x
Площадь образа области и длина образа кривой
Пусть w f z конформно отображает область D на область D . Тогда площадь
области D : S D dudv J dxdy f x, y dxdy .
2
D
D
D
Пусть – кривая, лежащая в области D , а – ее образ при отображении w f z .
Тогда длина кривой : l dw f z dz . .
20










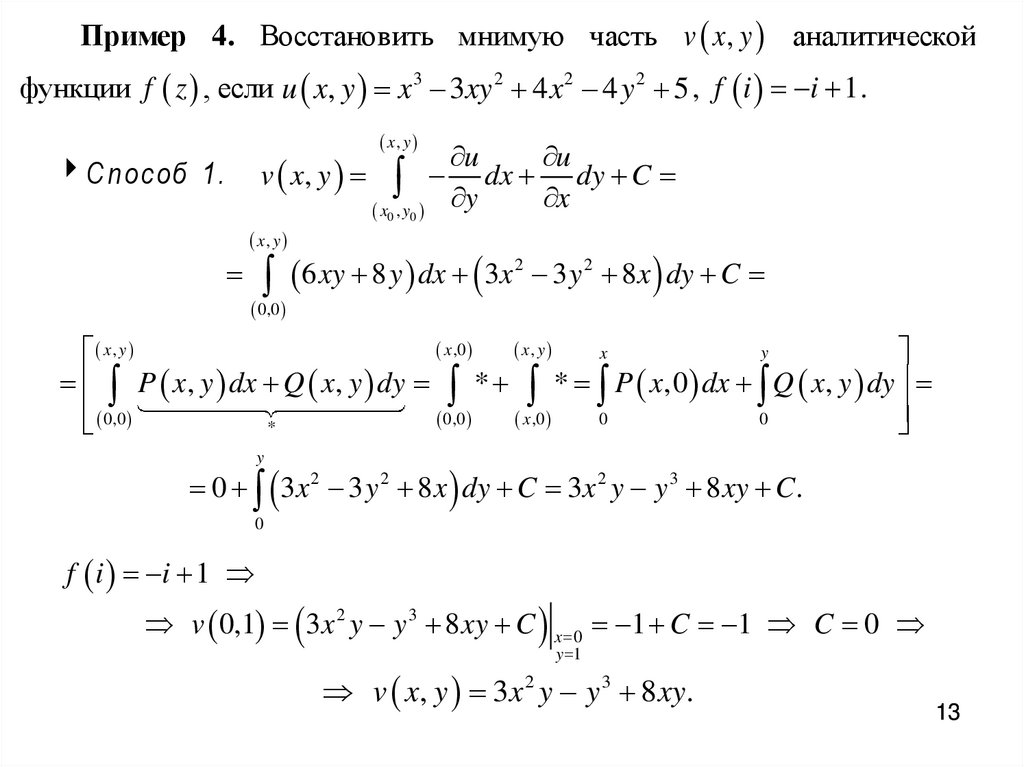
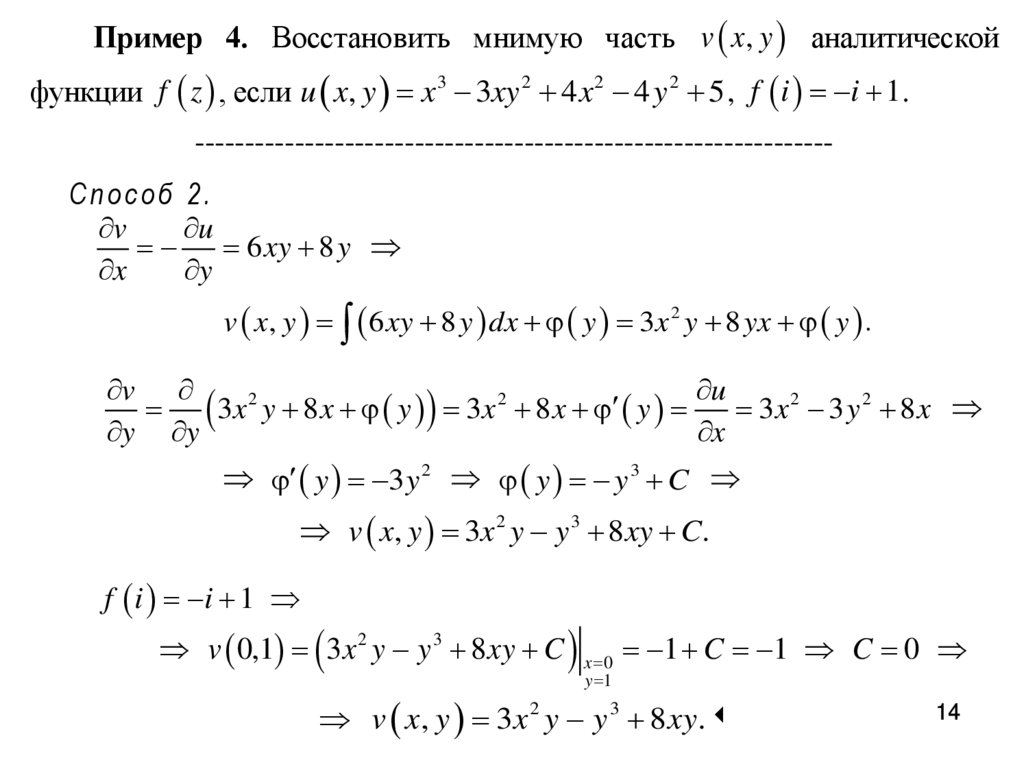





 mathematics
mathematics








