Основы математической статистики

1. ОСНОВЫ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

2.

Задачи математической статистики
Первая задача математической статистики - указать способы сбора и
группировки статистических сведений, полученных в результате
наблюдений или в результате специально поставленных экспериментов.
Вторая задача математической статистики - разработать методы
анализа статистических данных в зависимости от целей исследования:
а) оценка неизвестной вероятности события; оценка неизвестной
функции распределения; оценка параметров распределения, вид
которого известен; оценка зависимости случайной величины от одной
или нескольких случайных величин и др.;
б) проверка статистических гипотез о виде неизвестного
распределения или о величине параметров распределения, вид
которого известен.

3.

Генеральная и выборочная совокупности
Выборочной совокупностью или просто выборкой называют
совокупность
случайно
отобранных
объектов.
Генеральной
совокупностью называют совокупность объектов, из которых
производится выборка. Объемом совокупности (выборочной или
генеральной) называют число объектов этой совокупности.
Пусть из генеральной совокупности извлечена выборка, причем x1
наблюдалось n1 раз, х2 – n2 раз, xk - nk раз и ni n - объем выборки.
Наблюдаемые значения хi - называют вариантами, а
последовательность вариант, записанных в возрастающем порядке вариационным рядом. Числа наблюдений называют частотами, а
ni
Wi их отношения к объему выборки
относительными
n
частотами. Статистическим распределением выборки называют
перечень вариант и соответствующих им частот или относительных
частот.

4.

Эмпирическая функция распределения
Эмпирической функцией распределения (функцией распределения
выборки) называют функцию F * x
, определяющую для каждого
значения х относительную частоту события X < х.
Функцию распределения F(х)=P(X<x) генеральной совокупности
называют теоретической функцией распределения. Из теоремы
Бернулли следует, что относительная частота события X < х, т. е. F * x
стремится по вероятности к вероятности F(х) этого события. Отсюда
следует целесообразность использования эмпирической функции
распределения
выборки
для
приближенного
представления
теоретической (интегральной) функции распределения генеральной
совокупности.
Эмпирическая функция распределения выборки служит для оценки
теоретической функции распределения генеральной совокупности.

5.

ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Будем называть выборочной статистикой любую величину,
полученную в результате обработки данных эксперимента. Любая
выборочная статистика является случайной величиной.
Определение. Точечной оценкой параметра x называется его
приближенное значение x , полученное в результате обработки
выборки.
Определение. Оценка x параметра x называется несмещенной,
если математическое ожидание оценки совпадает с оцениваемым
параметром: M( x ) = х. Эффективной называют статистическую
оценку, которая (при заданном объеме выборки п) имеет наименьшую
возможную дисперсию.
Любая величина, определенная по выборке, называется статистикой.
Очевидно, что любая статистика – случайная величина.

6.

ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Определение. Оценка x параметра x называется состоятельной,
если при увеличении объема выборки n для любого 0 вероятность
отклонения оценки x
от параметра x на величину, меньшую ,
P x x 1
равна 1: nlim
Несмещенной и состоятельной оценкой математического ожидания
а оцениваемого
признака является выборочная средняя:
n
i , где - варианты выборки выходного параметра .
i 1
i
n
Несмещенной и состоятельной
оценкойn дисперсии D является
n
2
2
2
xi
выборочная дисперсия s :
xi x
2
n
s 2 i 1
n 1
i 1
n - 1 n
x
Выборочным средним квадратическим отклонением называют
2
s
s
величину:

7.

ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Медианой mе называют варианту, которая делит вариационный ряд
на две части, равные по числу вариант. Если число вариант нечетно, т. е.
xk xk 1
n = 2k+ 1, me = xk+1 , при четном n = 2k медиана me
.
2
Размахом варьирования R называют разность между наибольшей и
наименьшей вариантами: R = xmax – xmin .
Средним абсолютным отклонением называют
среднее
n
арифметическое абсолютных отклонений:
xi x
i 1
n
Коэффициентом вариации V называют выраженное в процентах
отношение выборочного среднего квадратического отклонения к
s
выборочной средней: V 100%
х

8.

ОЦЕНКА ПАРАМЕТРОВ РАСПРЕДЕЛЕНИЯ
Оценкой асимметрии теоретического распределения As
xi x
n
3
3
3
n
i 1
Ав
n - 1 n 2 s 3
является ее выборочное значение:
4
Оценкой теоретического эксцесса Ek 4 3 является его
выборочное значение:
xi x
n
n n 1
i 1
Eв
n 1 n 2 n 3
s4
4
3 n 1
n 2 n 3
2

9.

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
Доверительным интервалом для параметра называется интервал
( 1 , 2 ), накрывающий истинное значение с заданной
вероятностью = 1 - , то есть P 1 2 . Число = 1 -
называется доверительной вероятностью, а значение - уровнем
значимости. Статистики 1 и 2 , определяемые по выборке из
генеральной совокупности с неизвестным параметром , называются
нижней и верхней границами доверительного интервала (или левой и
правой границами).
Чтобы найти доверительный интервал для параметра , необходимо
~
~
знать закон распределения статистики x 1 , ... , x n , значение которой
является точечной оценкой параметра .
~
Пусть существует статистика Y Y , такая, что:
а) закон распределения Y известен и не зависит от ,
~
б) функция Y ,
непрерывна и строго монотонна по .

10.

ИНТЕРВАЛЬНОЕ ОЦЕНИВАНИЕ
Пусть = 1 - - заданная доверительная вероятность, а y y 1 и
2
2
y y 1 - квантили статистики Y порядков
и 1 . Тогда с
1
2
2
2
2
~
вероятностью = 1 - выполняется неравенство: y Y , y
2
Решая неравенство относительно , найдем границы 1 и 2
1
.
2
доверительного интервала для .
Распределение некоторых статистик для НСВ Х N(m, )
1 n
1. Выборочное среднее x x i
n i 1
N m ,
n
.
имеет нормальное распределение

11.

Распределение некоторых статистик для НСВ Х N(m, )
2. Выборочная дисперсия
1 n
s
xi x
n 1 i 1
2
величиной n 1 соотношением:
2
3. Статистика
x m
s
n
2
связана со случайной
s2
2
n 1
2 n 1
.
является случайной величиной, имеющей
распределение Стьюдента с (n – 1) степенью свободы Т(n – 1).
3. Пусть s 12 и s22 - выборочные дисперсии, вычисленные по
независимым выборкам объема n1 и n1 из двух нормально
распределенных генеральных совокупностей с дисперсиями 12 и 22 ,
тогда отношение
s12 12
s22
22
имеет распределение Фишера F n1 1, n2 1

12.

Доверительный интервал для среднего при известной
Пусть
x1 , ... , xn
- выборка n наблюдений случайной величины X N(m, ).
Рассмотрим статистику Y
u Y u
2
1
x m
n
N(0,1). Вероятность события
равна заданной доверительной вероятности , то есть
2
P u Y u
1
2
2
. Для квантилей стандартного (нормированного)
нормального распределения u u
2
1
. После решения неравенства
2
относительно m получим доверительный интервал в виде:
x
u
n
1
2
m x
u
n
1
2

13.

Доверительный интервал для дисперсии
В качестве оценки дисперсии используют выборочную дисперсию
x
2
n
1
s
n
2(n-1) .
s
x . Статистика Y
имеет
распределение
2
n - 1 n
n
i 1
2
2
i
Определим квантили 2 n 1 и
2
2
1
n 1 , удовлетворяющие условию
2
n 1 s 2
2
2
P n 1
n 1 1
2
1
2
2
Решая неравенство относительно 2, получим доверительный интервал
для дисперсии:
2
n 1 s 2
n
1
s
2
2
2
n 1
n 1
1
2
2

14.

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Статистической гипотезой Н называется предположение
относительно параметров или вида распределения случайной величины
Х. Если по выборке наблюдений необходимо проверить предположение
о значении параметров известного распределения, то такие гипотезы
называются параметрическими.
Проверяемая гипотеза называется нулевой гипотезой Н0. Вместе с
гипотезой Н0 рассматривают одну из альтернативных (конкурирующих)
гипотез Н1. Правило, по которому принимается решение принять или
отклонить гипотезу Н0, называется критерием. Статистика Z, на
основании которой принимается решение об истинности гипотезы Н0,
называют статистикой критерия.
Перед анализом выборки назначается некоторая малая вероятность
α, называемая уровнем значимости.

15.

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Пусть V – множество значений статистики Z, а Vk – такое
подмножество, что при условии истинности гипотезы Н0, вероятность
попадания статистики критерия в Vk равна α:
P Z Vk H 0
. α – уровень
значимости (малое число). Пусть zв – выборочное значение статистики Z,
вычисленное по выборке. Формулировка критерия: отклонить гипотезу
Н0, если z в Vk (попадание в критическую область); принять гипотезу
Н0, если z в V \ Vk (попадание в область принятия гипотезы).

16.

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Уровень значимости α определяет размер критической области Vk.
Положение критической области на множестве значений статистики Z
зависит от формулировки альтернативной гипотезы Н1. Если проверяется
гипотеза Н0: = 0, а альтернативная гипотеза Н1: > 0 ( < 0), то
критическая область размещается на правом (левом) хвосте плотности
распределения статистики Z, то есть имеет вид неравенства: Z z1
Z z , где
z1 и z - квантили распределения статистики Z ,
вычисленные при условии истинности Н0.

17.

ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ
Если альтернативная гипотеза
Н1: ≠ 0, критическая область
размещается на обоих хвостах
плотности распределения Z, то есть
определяется неравенствами:
Z z и Z z
.
В
этом
случае
2
1
2
критерий – двусторонний.
При проверке гипотез необходимо:
1. Сформулировать гипотезы Н0 и Н1 , назначить уровень значимости α.
2. Выбрать статистику Z критерия для проверки Н0.
3. Определить критическую область Vk, при условии, что верна Н0.
4. Вычислить выборочное значение статистики zв критерия.
5. Если z в Vk - отклонить Н0 , если z в V \ Vk
- принять Н0.
Размещение критической области при различных альтернативных гипотезах

18.

Сравнение двух дисперсий нормальных генеральных совокупностей
При заданном уровне значимости α по двум выборкам объемов n1 и
n1 проверить нулевую гипотезу H0 : D(X) = D(Y) о равенстве генеральных
дисперсий нормальных совокупностей при конкурирующей гипотезе
H1 : D(X) > D(Y). В качестве критерия выбирается отношение большей
дисперсии к меньшей
F
s Б2
2
sМ
F(n1 - 1, n2 - 1), имеющей распределение
Фишера (n1 – объем выборки с большей дисперсией). Критическая
область – односторонняя и определяется по правилу: F F1 n1 1, n2 1 ,
где F1 n1 1 ,n2 1 - квантиль распределения Фишера. Введем
критическое число Fкр F1 n1 1,n2 1 , отделяющее критическую
область от области принятия гипотезы.
Если Fнабл < Fкр – нет оснований отвергнуть нулевую гипотезу.
Если Fнабл > Fкр – нулевая гипотеза отвергается.

19.

Сравнение выборочной дисперсии с гипотетической генеральной
дисперсией нормальной совокупности
При заданном уровне значимости α по выборке объемом n проверить
2
нулевую гипотезу H0 : D(X) = 0 о равенстве генеральной дисперсии
D(X) гипотетическому значению 02 при конкурирующей гипотезе
n 1 s 2
2
2
H1 : D(X) > 0 . В качестве критерия выбирается статистика
2
0
имеющая распределение 2 с n -1 степенью свободы.
2
Наблюдаемое значение критерия вычисляется по выборке
2
набл
n 1 s
02
Критическая область - правосторонняя и определяется по правилу
n 1 , где 12 n 1 - квантиль распределения 2 с n -1 степенью
2
2
свободы порядка 1- α. Введем критическое число кр 1 n 1 .
2
2
Если набл кр - нет оснований отвергнуть нулевую гипотезу.
2
2
кр
Если набл
- нулевая гипотеза отвергается.
2
2
1

20.

Сравнение двух средних генеральных совокупностей, дисперсии которых
известны
При заданном уровне значимости α по двум выборкам объемами n и m
проверить нулевую гипотезу H0: M(X)=M(Y) о равенстве математических
ожиданий двух нормальных генеральных совокупностей с известными
дисперсиями при конкурирующей гипотезе H1: M(X) ≠ M(Y). В качестве
критерия выбирается статистика
x y
z
D X D Y
n
m
N(0,1).
Наблюдаемое значение zнабл критерия вычисляется по выборкам.
Критическая область - двусторонняя и определяется условиями
z u или z u
, где u - квантиль нормального нормированного
2
1
2
распределения порядка α. Учитывая, что
определяется неравенством z u
.
1
Если
zнабл zкр
u u
2
1
2
область принятия гипотезы
Пусть zкр u .
2
- гипотеза H0 принимается, иначе – отвергается.
1
2

21.

КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
Пусть по выборке случайной величины Х объема n необходимо
проверить гипотезу Н0 о том, что Х имеет предполагаемый закон
распределения. Пусть построена гистограмма для заданной выборки
случайной величины Х объема n с частичными интервалами j
одинакового размера h. По форме гистограммы делается
предположение о типе закона распределения и по выборке вычисляются
точечные оценки его параметров. Используя предполагаемый закон
распределения случайной величины Х, находим вероятности pj того, что
значение Х принадлежит частичным интервалам j, то есть p j P X j ,
где j = 1, ... , N. Величины mj = npj равны теоретическим частотам
попадания случайной величины Х в каждый частичный интервал.
Выборочное (наблюдаемое) значение статистики критерия вычисляется
по формуле:
N
( n j m j )2
j 1
mj
2
набл
2(N – mp – 1) .

22.

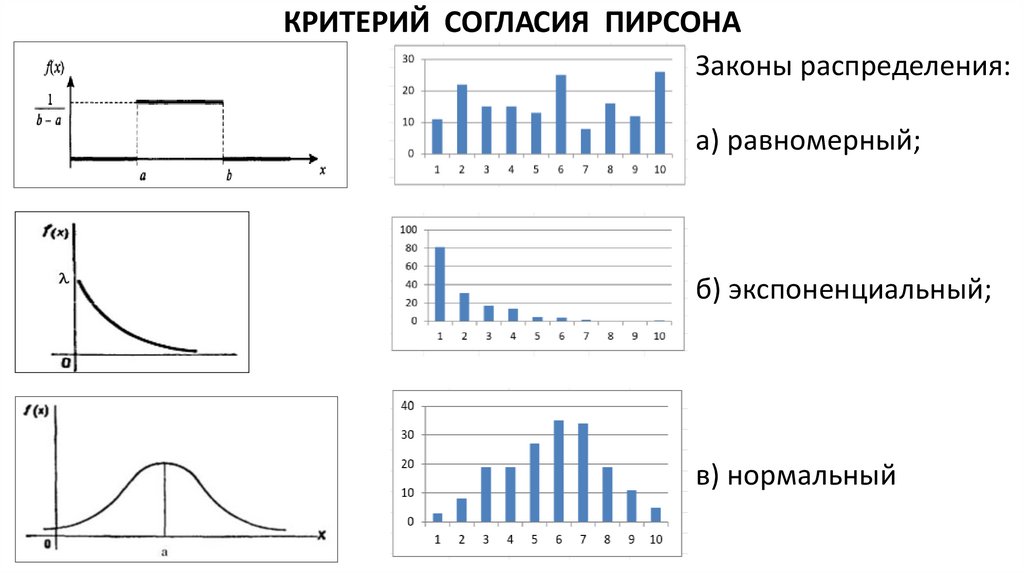
КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
Законы распределения:
а) равномерный;
б) экспоненциальный;
в) нормальный

23.

КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
Гипотеза Н0 согласуется с результатами наблюдений на уровне
2
12 N m p 1 , где 12 N m p 1 - квантиль порядка
значимости α, если набл
1 – α распределения 2 с N–mp–1 степенями свободы, где mp – число
неизвестных параметров распределения, оцениваемых по выборке.
2
2
Если же набл 1 N m p 1 , то гипотеза Н0 отклоняется.
При заданном уровне значимости используется следующий расчет.
1) Для каждого частичного интервала определяются средние точки yj
частичных интервалов.
2) Вычисляются теоретические частоты предполагаемого
распределения: а) для равномерного закона
hn
mj
, j 1 , ... , N ,
x max x min

24.

КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА
б) для нормального закона
( u )
1
2
x
2
hn
m j ( ui ) , j 1 , ..., N
s
, где
uj
y j xв
s
,
- плотность нормального нормированного распределения;
x
x
, j 1 , ..., N , где e
в) для показательного закона m j n e
в
2
e
в
j
в
j 1
выборочный параметр показательного закона распределения: в
Находится наблюдаемое значение критерия 2:
N
( n j m j )2
j 1
mj
2
набл
.
1
xв
.
3) Находится критическое значение критерия 2 по уровню значимости
и числу степеней свободы k = N - mp - 1, где mp - число параметров
распределения, равное mр = 2 для нормального и равномерного законов
2
12 N m p 1 .
mp = 1 для показательного распределения: крит
2
2
4) Если набл
крит - то выдвинутая гипотеза о типе закона распределения
не отвергается, иначе – принимается.

25.

МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ
Пусть есть результаты некоторого эксперимента (xi,yi), i = 1, ... , n. Надо
подобрать (“подогнать”) функцию y = f(x) = ax + b, наилучшим образом
описывающую экспериментальные точки ( xi , yi ). Критерием качества
“подгонки” кривойnвыберем минимум функционала:
F ( y i ( a bx i )) 2 min
i 1
Данный принцип называется методом наименьших квадратов и
является одним из самых распространенных методов подбора
функциональной зависимости, наилучшим образом описывающим
эмпирические данные.
F
F
Используя необходимые условия экстремума:
0,
0
n n
n x i yi - x i yi
1 n
b*
i 1
i 1
i 1
*
*
b
, a yi
2
n
n
n i 1
n
2
n x i x i
i 1
i 1
a
n
Получим:
n
xi
i 1
b

26.

МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ
Введем обозначения:
*
x1
y1
1
1
x2
y2
x
, y
, s
1
x
y
n
n
Тогда y a s b x - вектор “подогнанных” с помощью регрессионного
уравнения
значений
у,
лежащий
в
плоскости
(гиперплоскости)
векторов
*
e
y
y
s
x и ;
- вектор разности между выборочными значениями у и
“подогнанными”
с помощью функции y = f(x). Наилучшее приближение
*
y к y будет, если вектор e перпендикулярен обоим векторам x и s :
равенству
нулю
двух
e s , e x . Это условие эквивалентно
Т
Т
скалярных произведений: s e 0 и x e 0 . Обозначим:
1
1
X
1
x1
x2
, ab .
x n
Тогда e y X .

27.

МОДЕЛЬ ПАРНОЙ
РЕГРЕССИИ
s
Условие
ортогональности
вектора
к
плоскости
векторов
и
:
x
e
1
T
T
T
.
После
преобразований:
X
X
X
y . Это уравнение для
X e 0
коэффициентов регрессионного уравнения a и b совпадает с формулами
по методу наименьших квадратов.
Пусть реальное (теоретическое) уравнение зависимости y от х имеет
вид: y = a + bx + , где х - неслучайная (детерминированная) величина, у
и - случайные величины. Считаем,, что N(0, ), где 2 - дисперсия
ошибок. По данным наблюдений следует найти оценки a* и b* для
коэффициентов уравнения регрессии и s2 - для дисперсии ошибок 2.
Имеет место теорема Гаусса-Маркова, утверждающая, что при
использовании метода наименьших квадратов для определения
оценок
1
T
*
*
a и b коэффициентов уравнения регрессии по формуле X X X T y
полученные оценки являются несмещенными и эффективными в классе
всех несмещенных оценок (то есть имеют наименьшую дисперсию).

28.

МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ
В соответствии с теоремой Гаусса-Маркова оценки a* N(a, a),
b* N(b, b) . Имеют
место следующие формулы для дисперсий оценок:
n
D( a
*
) a2
yi a
n
s 2 i 1
*
xi2
i 1
2
2
n 2
n x i n x
i 1
b xi
n 2
*
*
, D( b
) b2
2
n
xi2 n x
i 1
2
.
Оценки дисперсий:
n
xi2
2
, sa2 s 2
i 1
n x i2 n x
i 1
n
2
, sb2
s2
xi2 n x
n
2
.
i 1
При проверке гипотезы: H0: b = b0 с альтернативой H1: b b0
используется статистика t
b* b0
sb
, имеющая распределение Стьюдента с
(n - 2) степенями свободы. Доверительный интервал для коэффициента b
с надежностью : b b* t sb ; b* t sb где t - квантиль распределения
Стьюдента, определяемый из условия: P( | t | < t ) = .

29.

МОДЕЛЬ ПАРНОЙ РЕГРЕССИИ
Доверительный интервал для коэффициента а с надежностью имеет
вид: a a* t sa ; a* t sa .
Коэффициентом детерминации (или долей объясненной
дисперсии)
n
ESS TSS ESS RSS
2
называется величина: R 1
, где TSS ( yi y )2 ,
TSS
TSS
TSS
n
n
i 1
, RSS ( y ) . Очевидно, что 0 R2 1. Если, R2 = 0, то
i 1
i 1
регрессия не улучшает качество прогноза у по сравнению с
тривиальным: y y . Если R2 = 1, то это означает точную “подгонку”: все
наблюдаемые точки лежат на регрессионной кривой.
Проверяется
гипотеза H0: b = b0 с альтернативой H1: b b0. Статистика
n
ESS ( yi
y*i
)
2
y*i
2
( y*i y )2
F(1; n - 2). Если при заданном уровне значимости
s
критическое значение Fкр( ; 1; n - 2) меньше наблюдаемого значения
F i 1
2
Fнабл , то гипотеза Н0 - отвергается и имеет место зависимость у от х, то
есть регрессия улучшает прогноз по сравнению с тривиальным: y y .

30.

МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
2+...+ xk+ ,
Рассматривается
следующее
уравнение
модели:
y=
+
x+
x
0
1
2
k
Т
...
где
- вектор коэффициентов модели, х1 , х2 , ... , хk 1
2
k
регрессоры (независимые переменные), - случайная компонента,
N(0, ), где 2 - дисперсия ошибок. По результатам экспериментов
(xi ; yi ), i = 1, ... , n надо определить значения коэффициентов i .
Пусть
1 x x2
y1
1
1
2
y
1
x
x
2
2
y 2 , X
...
... ... ...2
y
n
1 xn xn
y*
... x1k
1
k
... x 2 , y* y*2
...
... ...
*
... x nk
yk
, где
y *i 0 1 x i 2 x i2 ... k x ik
*
y
...
прогноз значений объясняемой переменной.
Пусть
вектор прогнозируемых значений. Тогда e y y* - вектор разности
между выборочными
и прогнозируемыми значениями y. Будем
находить вектор 2 из условия минимизации
длины вектора e из
T
соотношения: e eT e y y* y y*
y1
y 2
Т
yk
-
-

31.

МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Для оценки коэффициентов множественной регрессии необходимо
использовать
формулу,
совпадающую
со
случаем
парной
регрессии:
1
*
T
T
X X X y . Формула для оценки дисперсии ошибок 2 :
s2
T
e e
n ( k 1)
. Коэффициент детерминации
определяется
так
же,
как
и
n
2
для парной регрессии:
R2
y*i y
RSS i 1
n
TSS
y y
2
i
i 1
T
y n y
X y n y
T
T
y
2
2
Для определения дисперсий оценок коэффициентов
регрессии
*
1
2
T
вычисляется матрица ковариаций: V s X X . В качестве
дисперсий оценок:
*
D s12 s22 ... sk2
берутся диагональные
Т
элементы qii матрицы V * : si2 s 2 qii . Доверительный интервал для
коэффициентов регрессии i : i i* t si ; i* t si , где t T(n-(k-1)).

32.

МОДЕЛЬ МНОЖЕСТВЕННОЙ РЕГРЕССИИ
Для проверки значимости коэффициентов регрессии i можно
использовать гипотезу H0: i = 0 при альтернативе H1: i 0.
i*
tкр ,
Двусторонняя критическая область формируется из условия t
si
где tкр( ; n - (k + 1)) - критическая точка распределения Стьюдента для
уровня значимости и числа степеней свободы n - (k + 1) .
Для оценки значимости уравнения регрессии, то есть проверки факта
улучшения прогноза значения у по сравнению с тривиальным: y y
используется критерий Фишера. Гипотеза H0: 1 = 2 = ... = k = 0
(свободный член
0 - не учитывается) проверяется с использованием
n
( y*i y )2 k
i 1
F
s2
статистики
F(k; n - (k + 1)) . Если наблюдаемое значение
Fнабл больше критического Fкр( ; k; n - (k + 1)), то гипотеза Н0 отвергается.

33.

"ПОДГОНКА" КРИВОЙ
Пусть данные некоторого эксперимента представлены в виде таблицы
значений переменных x и y. Ставится задача об отыскании
аналитической зависимости между x и y, то есть некоторой формулы
y = f(x), явным образом выражающей y, как функцию х. Естественно
требовать, чтобы график искомой функции y = f(x) не слишком уклонялся
от экспериментальных точек (xi , yi ). Эту задачу называют сглаживанием"
экспериментальных данных или "подгонкой" кривой. Для решения
можно использовать метод наименьших квадратов (МНК). Согласно МНК
указывается вид эмпирической формулы y = Q(x, a0 , a1 , … , an), где a0 , a1
, … , an – числовые параметры. Наилучшими значениями параметров a0 ,
a1 , … , an считаются те, для которых сумма квадратов уклонений функции
y = Q(x, a0 , a1 , … , an) от экспериментальных
точек (xi , yi ) , i = 1, 2, … , m
m
является минимальной S(a0 , a1 ,..., an ) (Q( xi , a0 , a1 ,..., an ) y i )2 min
i 1

34.

"ПОДГОНКА" КРИВОЙ
Используя необходимые условия экстремума функции нескольких
переменных, получаем систему уравнений для определения параметров
S
S
S
0,
0 , ... ,
0 . Если система имеет единственное решение, то оно
a 0
a 1
a n
является искомым и аналитическая зависимость между
экспериментальными данными определяется формулой: y = f(x). В
общем случае система уравнений для определения оптимальных
значений параметров нелинейна.
Пусть для переменных x и y соответствующие значения
экспериментальных данных (xi , yi ) не располагаются вблизи прямой.
Тогда можно выбрать новые переменные X = (x, y) и Y = (x, y) так,
чтобы преобразованные экспериментальные данные Xi = (xi , yi ) и
Yi = (xi , yi ) в новой системе координат (X, Y) давали точки (Xi , Yi) ,
менее уклоняющиеся от прямой Y = kX + b.

35.

"ПОДГОНКА" КРИВОЙ
Числа k и b определяются по встроенной функции ЛИНЕЙН, где
вместо xi и yi подставляют соответствующие значения Xi и Yi.
Функциональная зависимость y = f(x) определена неявно уравнением
(x, y) = k (x, y) + b, которое разрешимо относительно y в частных
случаях.
Рассмотрим семь вариантов преобразования переменных, в которых
возможно явное выражение переменной y из уравнения
(x, y) = k (x, y) + b. В таблице приведены формулы преобразования
переменных, явная эмпирическая формула y = f(x), зависящая от двух
параметров и , выражение этих параметров через коэффициенты,
полученные с помощью МНК.

36.

"ПОДГОНКА" КРИВОЙ

37.

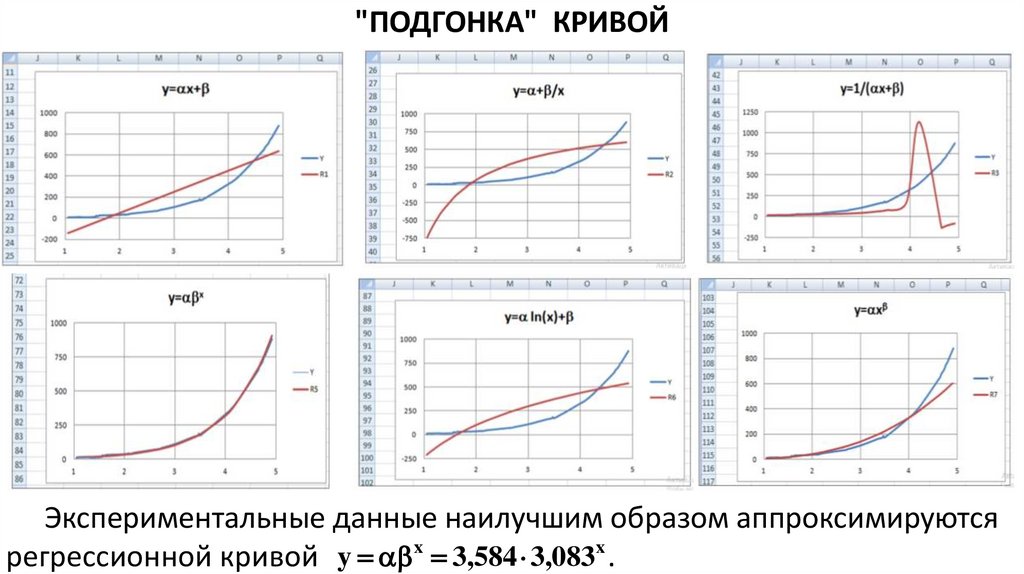
"ПОДГОНКА" КРИВОЙ
Экспериментальные данные наилучшим образом аппроксимируются
регрессионной кривой y x 3,584 3,083x .