Similar presentations:
Математическая логика
1.
Математическая логика2. Идеи математической логики
1) Предполагается, что все слова обычного языкаи предложения можно записать математическими
знаками
2) Все рассуждения можно заменить вычислением
3) Применить математические методы для оценки
справедливости рассуждений
3. Основы
«Аналитики» Аристотеля (384-322 гг. до н.э)."Первые аналитики" содержат теорию силлогизмов
Пример силлогизма:
Всякий человек смертен (бо́льшая посылка)
Сократ — человек (меньшая посылка)
----------- Сократ смертен (заключение)
"Вторые аналитики" содержат теорию доказательств
4. Этапы развития
Замыселуниверсального
Лейбниц (1646-1716)
логического
исчисления
развивал
Начало создания аппарата математической логики, который
теперь мы называем логикой высказываний, положил Джордж
Буль (1815-1864)
Логико-математические языки и теория их смысла были затем
значительно развиты в работах Фреге (1848-1925)
В работах Пеано (1858-1932) и особенно Рассела и Уайтхеда,
изданных в 1910-1913 годах, представлено изложение основных
разделов математики на языке математической логики
В 20-ых годах XX века — с программой обоснования
математики на базе математической логики выступил Гильберт
(1862-1943)
5. Обоснование математики
Математическую теорию уточняют и описываютна базе строгого логико-математического языка
(формализация теории)
Построенная теория исследуется на
непротиворечивость
полноту
разрешимости
6. Логические представления
Логические(формальные)
представления
исследуемой системы — это ее описание в виде
совокупности сложных высказываний, составленных
из простых (элементарных) высказываний и
логических связок между ними.
Логические
представления
характеризуются
определенными свойствами и набором допустимых
преобразований над ними (операций, правил вывода и
т.п.), которые являются правильными методами
рассуждений — законами логики.
7. Предмет изучения
Способы (правила) формального логическогопредставления высказываний, построения новых
высказываний из имеющихся с помощью
логически выдержанных преобразований
Способы (методы) установления истинности
или ложности высказываний.
8. Разделы МЛ
Современная логика состоит из двух разделовлогика высказываний
логика предикатов
Для построения логики существует два основных
подхода (языка):
алгебра логики
исчисление логики
9.
Логика высказываний10. Основные определения
Высказывание — повествовательное предложение (утверждение,суждение), о котором имеет смысл говорить, что оно истинно
или ложно. Пример: «Дважды два четыре», «На улице жара».
Все научные знания, события повседневной жизни, ситуации в
экономике, управлении, политике формируются в виде
высказываний.
Простые высказывания рассматриваются в данном контексте
как неделимое целое (аналогично элементу множества)
Сложные высказывания формулируются из простых с помощью
логических связок (логических операций), заменяющие связки
естественного языка в сложных предложениях.
11. Логические связки (операция)
Логическая операция - это функция видаf(x1,x2,…xn): Bn→B, где В множество состоящее
из двух элементов В={0,1}.
Логическая операция – это функция зависящая от
логических переменных (т.е. принимающих
значение 0,1), которая так же может принимать
только два значения 0 и 1.
В таблице истинности для бинарных операций
первые два столбца содержат все возможные
наборы операндов, а последующие столбцы
значение логических функций.
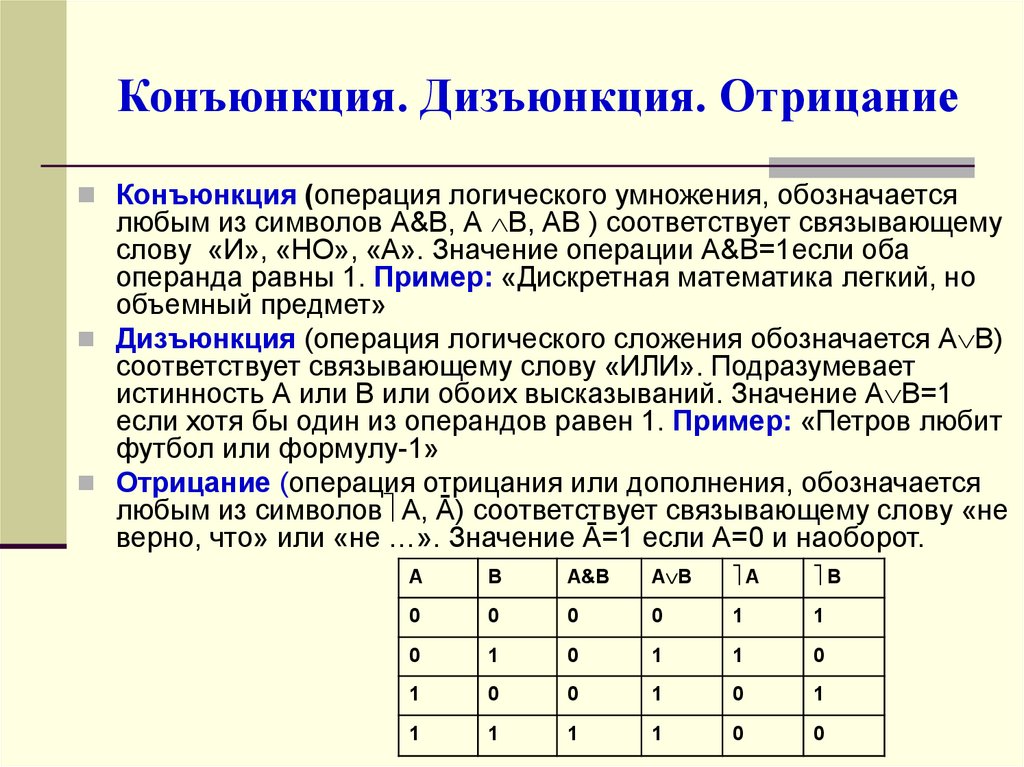
12. Конъюнкция. Дизъюнкция. Отрицание
Конъюнкция (операция логического умножения, обозначаетсялюбым из символов А&В, А В, АВ ) соответствует связывающему
слову «И», «НО», «А». Значение операции А&B=1если оба
операнда равны 1. Пример: «Дискретная математика легкий, но
объемный предмет»
Дизъюнкция (операция логического сложения обозначается А В)
соответствует связывающему слову «ИЛИ». Подразумевает
истинность А или В или обоих высказываний. Значение А В=1
если хотя бы один из операндов равен 1. Пример: «Петров любит
футбол или формулу-1»
Отрицание (операция отрицания или дополнения, обозначается
любым из символов А, Ā) соответствует связывающему слову «не
верно, что» или «не …». Значение Ā=1 если А=0 и наоборот.
А
B
А&B
A B
А
В
0
0
0
0
1
1
0
1
0
1
1
0
1
0
0
1
0
1
1
1
1
1
0
0
13. Разделительное ИЛИ. Эквивалентность
Разделительное ИЛИ (обозначается ХОR, 2)соответствует фразам «ИЛИ», «Либо … либо» в
разделительном смысле. Значение А 2 В =1 если значение
операндов различно. Например: «Студент Иванов сдаст
экзамен по дискретной математике или не сдаст».
Эквивалентность (обозначается А В) соответствует связкам
«А эквивалентно В», «А равносильно В», «А тоже, что и В»,
«А тогда и только тогда, когда В», «А необходимо и
достаточно для В». Значение А В=1, Если А=В. Например:
«Деление числа k на 2 и 3 (А) необходимо и достаточно для
деления k на 6 (В)».
«Любое число делится на 6 (А) тогда и только тогда, когда
оно делится на 2 и 3 (В)».
А
B
А 2 B
A~B
0
0
0
1
0
1
1
0
1
0
1
0
1
1
0
1
14. Импликация
Условные высказывания типа «если А, то В», «Авлечет В» соответствуют логической операции
импликация. Обозначается следующим образом
А В. Пример: отец говорит сыну: «Если в этом
семестре ты сдашь все экзамены на «отлично» (A),
то я куплю тебе машину (B)». При каких условиях
отец говорит правду?
А
B
A B
0
0
1
0
1
1
1
0
0
1
1
1
Одинаковый ли смысл имеют высказывания?
«Если человек усердно работает, то он добьется успеха»
«Человек добьется успеха если он усердно работает»
Неважно в каком порядке присутствуют простые высказывания.
Важно какое высказывание соответствует условию.
15. Конверсия, инверсия, контрапозиция высказывания АВ
Конверсия, инверсия,контрапозиция высказывания А В
Пусть определена импликация
А В, тогда для этого
выражения можно построить
Конверсию В А
А В
Контрапозицию В А
Инверсию
А
B
А B
В А
А В
В А
0
0
1
1
1
1
0
1
1
0
0
1
1
0
0
1
1
0
1
1
1
1
1
1
Высказывания являются равносильными если для каждого набора
переменных совпадают их значения.
Равносильны:
Конверсия В А и инверсия А В
Импликация А В и контрапозиция В А
16. Необходимые и достаточные условия
Импликации A B, кроме очевидных «Если А, то В», «Авлечет В», соответствуют следующие словесные обороты:
«А достаточно для В»: «Делимость числа на 12 достаточное
условие для делимости числа на 6». При выполнении А
(делимости на 12) всегда наступает В (делимость на 6) A B.
Равносильно «Если число делится на 12, то оно делится на 6».
«В необходимо для А»: «Делимость числа на 2 необходимое
условие делимости числа на 6. Не выполнение В (на 2 не
делится) влечет не выполнение А (на 6 не делится), т.е.
выполняется контрапозиция В А. Как показано раннее,
контрапозиция равносильна импликации A B. «Если k
делится на 6, то оно делится на 2».
17. Примеры необходимых и достаточных условий
Пусть число k делится на 12 определить какиеусловия являются необходимыми (Н), достаточными
(Д), необходимыми и достаточными (НИД)
Н
Д
НИД
Число делится на 2
+
Число делится на 3
+
Число делится на 4
+
Число делится на 6
+
Число делится на 24
+
Число делится на 36
+
Число делится на 2 и 3 +
Число делится на 3 и 4 +
+
+
18. Логическая формула
Буквы, обозначающие высказывания, логические связки искобки составляют алфавит языков логики высказываний:
алгебры высказываний и исчисления высказываний. С
помощью
элементов
алфавита
можно
построить
разнообразные логические формулы.
Будем называть выражение, составленное из обозначений
высказываний и связок (а также скобок), — логической
формулой, если оно удовлетворяет следующим
условиям:
любая переменная, обозначающая высказывание, —
формула;
если A и B — формулы, то (A & B), (A B), ( A), (A B),
(A ~ B), (A B) — формулы;
других формул нет.
19. Логически правильные рассуждения
Наряду с алфавитом и правилами построения сложныхвысказываний
(логических
формул),
языки
логики
высказываний
содержат
правила
преобразования
логических формул.
Правила
преобразования реализуют общелогические
законы
и
обеспечивают
логически
правильные
рассуждения.
Корректность
допустимых
в
логике
преобразований является фундаментальным свойством
формальной (математической) логики.
Процесс
получения
новых
знаний,
выраженных
высказываниями, из других знаний, также выраженных
высказываниями,
называется
рассуждением
(умозаключением).
Исходные
высказывания
называются
посылками
(гипотезами, условиями), а получаемые высказывания —
заключением (следствием).
20. Правило заключения — утверждающий модус (Modus Ponens):
«Если из высказывания A следуетвысказывание B и справедливо (истинно)
высказывание A, то справедливо В».
Обозначается:
Для построения логических формул,
отражающих логически правильные
((A B)&A) B
рассуждения, следует все посылки
соединить конъюнкцией & и полученную таким образом обобщенную
посылку связать импликацией с выводом
Рассуждение А→В, В НЕ является логически правильным.
А
Выделены клетки, соответствующие
А
В
A B Истинны
Истинны
наборам переменных при которых
A B, А
A B, В
истинны обе посылки.
A B, A
B
0
0
1
0
1
1
1
0
0
1
1
1
Во втором рассуждении истинным
значениям посылок соответствуют
А=0 и А=1, следовательно нельзя
утверждать, что А- верно.
21. Пример анализа рассуждений
«Если рабочий отсутствовал на работе (А), то он не выполнилзадание (В). Рабочий не выполнил задание. Следовательно, он
отсутствовал на работе».
Схема рассуждений А→В, В Данное рассуждение НЕ является
А
логически правильным
Логически правильным будет рассуждение
А→В, А
«Если рабочий отсутствовал на работе (А), то
В
он не выполнил задание (В). Рабочий отсутствовал на работе.
Следовательно, он не выполнил задание».
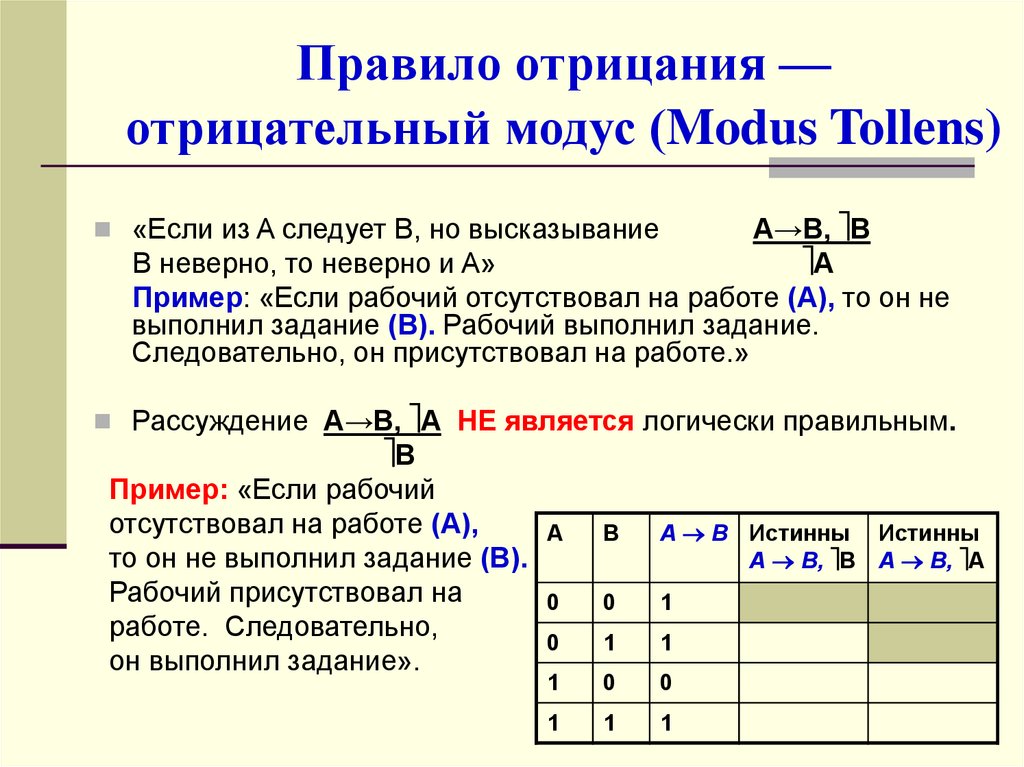
22. Правило отрицания — отрицательный модус (Modus Tollens)
А→В, ВВ неверно, то неверно и A»
А
Пример: «Если рабочий отсутствовал на работе (А), то он не
выполнил задание (В). Рабочий выполнил задание.
Следовательно, он присутствовал на работе.»
«Если из A следует B, но высказывание
Рассуждение А→В, А НЕ является логически правильным.
В
Пример: «Если рабочий
отсутствовал на работе (А),
то он не выполнил задание (В).
Рабочий присутствовал на
работе. Следовательно,
он выполнил задание».
А
В
A B Истинны Истинны
A B, В A B, А
0
0
1
0
1
1
1
0
0
1
1
1
23. Правило утверждения–отрицания (Modus Ponendo–Tollens):
«Если справедливо или высказывание A,или высказывание B (в разделительном
смысле) и истинно одно из них, то другое
ложно»
A B, A
B
A B, B
A
24. Правило отрицания–утверждения (Modus Tollen–Ponens):
«Если истинно или A, или B (в разделительномсмысле) и неверно одно из них, то истинно другое»
A B , A
B
A B , B
A
«Если истинно A или B (в неразделительном смысле)
и неверно одно из них, то истинно другое»
A B , A
B
A B , B
A
25. Правило транзитивности (упрощенное правило силлогизма)
«Если из A следует B, и из B следует C, тоиз A следует C»
A B, B C
A C
26. Закон противоречия:
«Если из A следует B и B, то неверно A»A B , A B
A
27. Правило контрапозиции:
«Если из A следует B, то из того, чтоневерно B, следует, что неверно A»
A B
B A
28. Правило сложной контрапозиции:
«Если из A и B следует С, то из А и Сследует B»
( A & B) C
( A & C ) B
29. Правило сечения:
«Если из A следует B, а из В и С следует D,то из А и С следует D»
A B, ( B & C ) D
( A & C) D
30. Правила импортации (объединения) и экспортации (разъединения) посылок:
A (B C)( A & B) C
( A & B) C )
A (B C)
31. Правило дилемм:
A C, B C, A BC
A B , A C , B C
A
A B , C D, A C
B D
A B , C D , B D
A C
32. Сведение к абсурду (Reductio ad Absurdum)
Если из того, что А не верно, следует, что В верно и не верноодновременно, то А верно
А →( В & B )
А
Сведение к абсурду используется в методе
доказательства, известном как доказательство от
противного. Оно состоит в следующем
Предполагается, что истинным является отрицание того
высказывания, которое необходимо доказать. Затем
необходимо прийти к противоречию. Если это удается,
то исходное утверждение доказано.
33. Алгебра логики (высказываний)
Математическая логика состоит из двух разделов: логикивысказываний и логики предикатов.
Логика высказываний может быть представлена двумя
подходами: алгеброй логики (высказываний) и исчислением
высказываний.
Алгебра, образованная множеством B={0,1} вместе со всеми
возможными операциями на нем, называется алгеброй
логики.
Алгебра логики как раздел математической логики изучает
строение сложных логических высказываний (логических
формул) и способы установления их истинности с помощью
алгебраических методов.
34. Основные объекты
Формулы алгебры логики состоят избукв — логических (двоичных) переменных
знаков операций — логические операции (логические связки)
скобок
Каждая формула задает логическую функцию — функцию
от логических переменных (т.е. принимающих значение 0,1),
которая так же может принимать только два значения 0 и 1.
Другими словами логическая функция имеет вид f(x1,x2,…xn):
Bn→B, где В множество состоящее из двух элементов В={0,1}.
Множество всех логических функций обозначается P2,
множество всех логических функций n переменных — P2(n).
Число |P2(n)| различных функций n переменных равно числу
различных двоичных векторов длины 2n, т.е.
P2 (n) 2
2n
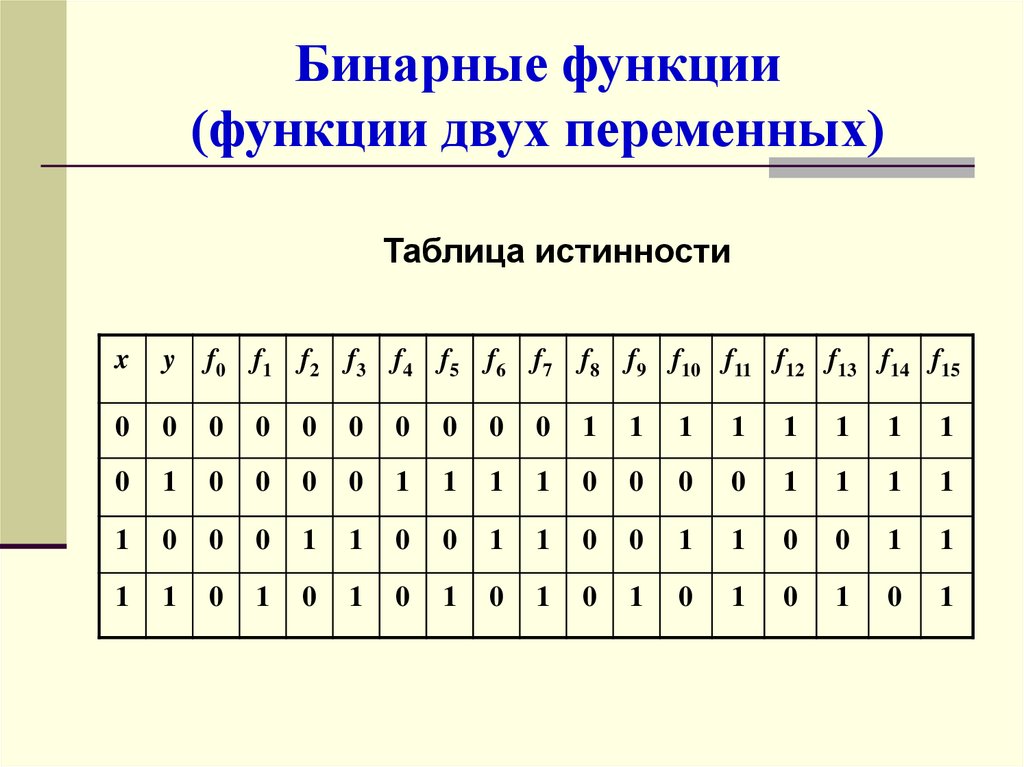
35. Бинарные функции (функции двух переменных)
Таблица истинностиx
y
f0 f1 f2 f3 f4 f5 f6 f7 f8 f9 f10 f11 f12 f13 f14 f15
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
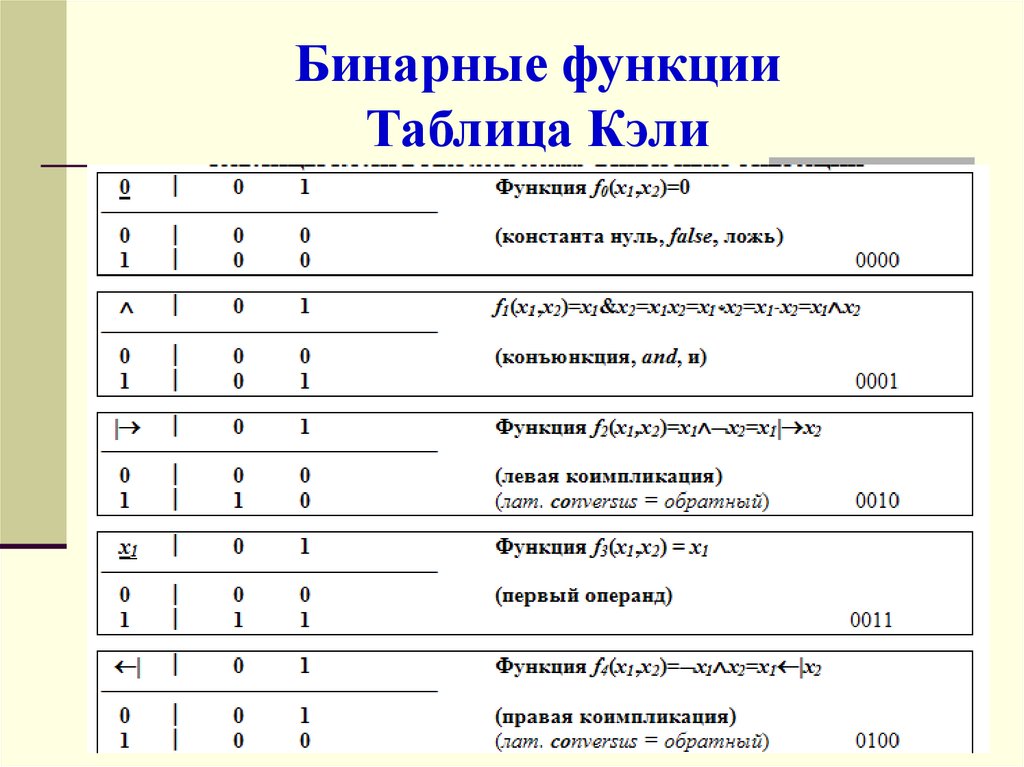
36. Бинарные функции Таблица Кэли
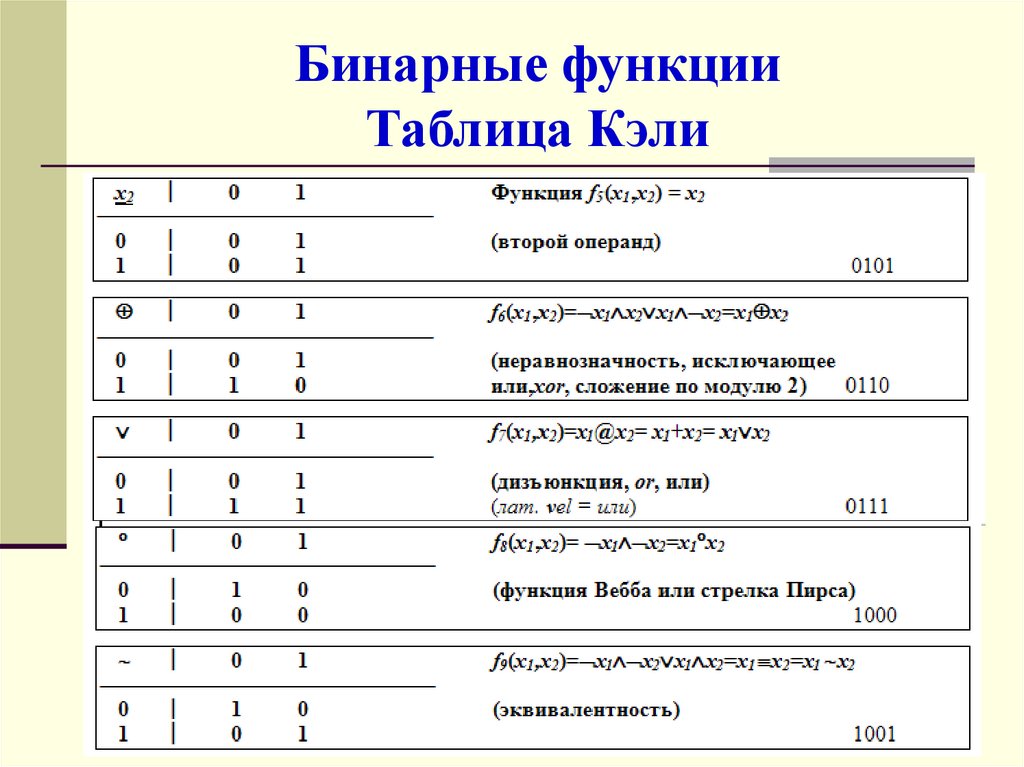
37. Бинарные функции Таблица Кэли
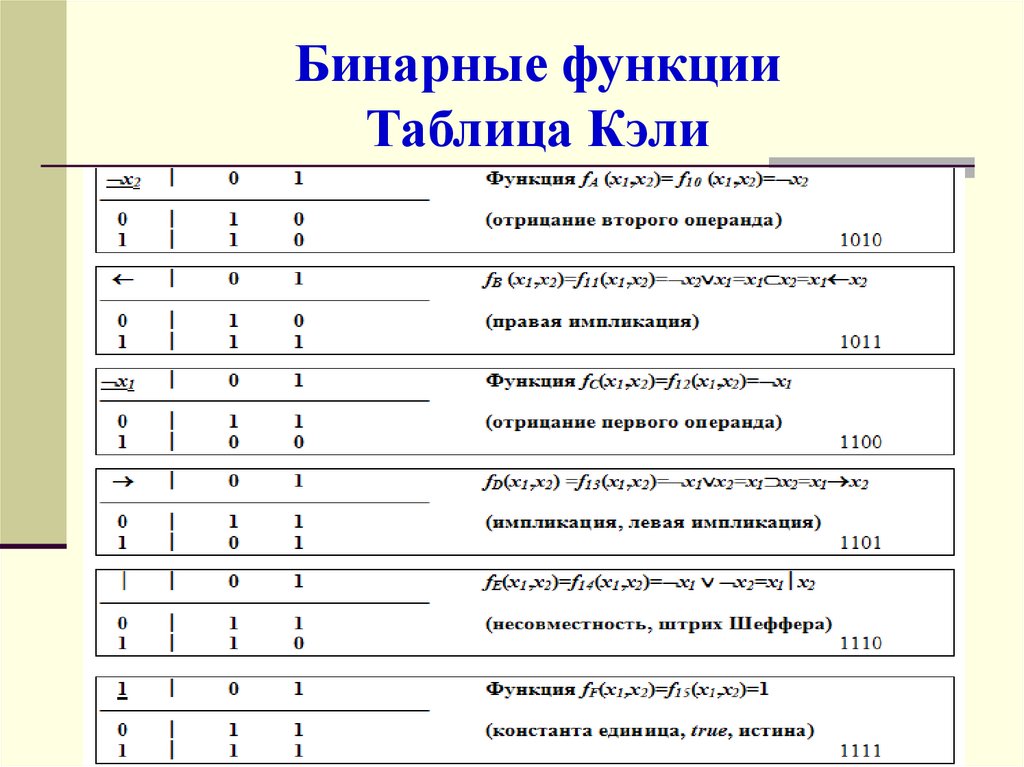
38. Бинарные функции Таблица Кэли
39. Фиктивные переменные
Переменная xi в функции f(x1,…, xi–1, xi, xi+1, …, xn)называется несущественной (или фиктивной), если
f(x1,…, xi–1, 1, xi+1, …, xn) = f(x1,…, xi–1, 0, xi+1, …, xn) при
любых значениях остальных переменных.
В этом случае f(x1,…, xn) по существу зависит от n - 1
переменной, т.е. представляет собой функцию g(x1,…,
xi–1, xi+1, …, xn) от n - 1 переменной.
Говорят, что функция g получена из функции f
удалением фиктивной переменной, а функция f
получена из функции g введением фиктивной
переменной, причем эти функции по определению
считаются равными































 mathematics
mathematics








