Similar presentations:
Теория матричных игр
1. Теория матричных игр
2.
Основные понятия теории матричных игрТеория игр – математическая теория конфликтных ситуаций,
целью которой является выработка рекомендаций по разумному
поведению участников конфликта.
Конфликтная ситуация – это столкновение интересов двух
или более сторон.
Игра – это математическая модель конфликтных ситуаций, а
также система предварительно оговоренных правил и условий.
Партией называется частичная реализация правил и
условий игры. Результатом игры всегда является число v,
которое называется выигрышем, проигрышем или ничьей.
если υ > 0 – выигрыш
если υ < 0 – проигрыш
если υ = 0 – ничья
3.
Партии состоят из ходов. Ходом называется выбор игрокомодного из предусмотренных правилами игры действий и его
осуществление.
Ходы бывают:
личными – когда игрок сознательно выбирает и осуществляет
тот или другой вариант действия (пример –– любой ход в шахматах);
случайными – когда выбор осуществляется не волей игрока, а
каким-то механизмом случайного выбора (бросание монеты,
игральной кости).
Игры бывают:
парные – игра между двумя игроками;
множественные – в них участники могут образовывать коалиции
(постоянные или временные);
кооперативные – играют более двух человек, которые образуют
кооперации до конца игры;
коалиционные – объединение, но не до конца игры;
не коалиционные – с начала и до конца каждый играет сам за
себя.
4.
Стратегией игрока называется совокупность правил,определяющих выбор варианта действий при каждом личном
ходе в зависимости от сложившейся ситуации. В зависимости от
стратегий игры делятся на конечные и бесконечные.
Игра называется конечной, если у каждого игрока имеется в
распоряжении только конечное число стратегий (в противном
случае игра называется бесконечной).
Игра с нулевой суммой – это игра, в которой сумма
выигрышей игроков равна нулю (т.е. каждый игрок выигрывает
только за счет других). Самый простой случай – парная игра с
нулевой суммой – антагонистическая игра, здесь два игрока
четко играют друг против друга.
Игры бывают с полной информацией, в этом случае игроки
четко знают все правила игры и четко знают все шаги
противника, и с неполной информацией.
5.
Результат игры записывается в платежную матрицу.Игра «орел - решка»
B1 “орел”
B2 ” решка”
A1 ” орел”
1
-1
A2 ” решка”
-1
1
Нижней чистой ценой игры называется
max min aij
Верхней чистой ценой игры называется
min max aij
j
i
j
i
6.
Игра, для которойгде
v
,
называется игрой с седловой точкой,
называется ценой игры.
Элемент, стоящий на пересечении и , называется
седловым элементом матрицы.
Задача теории игр – поиск оптимальных стратегий (решений).
Решением игры называется пара оптимальных стратегий для
игроков А и В, значение цены игры.
Наличие седловой точки означает наличие равновесия в игре.
7.
Чистые и смешанные стратегииЧистой
стратегией
называют
ход,
выбранный
вероятностью 1.
Смешанной стратегией игрока А называется вектор
m
р ( р1 ,...... рm ) рi 0 (i 1, m),
p
i 1
i
1
Смешанной стратегией игрока В называется вектор
q (q1 ,......qn ) q j q ( j 1, n),
m
n
q
j 1
n
j
1
f ( p, q) aij p. i q j платежная функция.
i 1 j 1
Рi (0,0,0,...,1,0...) чистая стратегия
Пара стратегий
р , q
называется оптимальной, если
f ( p, q ) f ( p , q ) f ( p , q).
с
8.
Теорема1Средний выигрыш или проигрыш лежит между
и .
Теорема 2 (основная теорема теории игр). В терминах
смешанных стратегий любая конечная игра имеет решение.
Теорема 3 Для того, чтобы смешанные стратегии
p ( p1 ,...... pm ) q (q1 ,......qn ) были оптимальными в матричной игре
( a ij ) m n , необходимо и достаточно :
m
a p
ij i
i 1
n
a q
ij j
j 1
( j 1,n),
(i 1,m).
9.
q1 q2 qnp1 a11 a12 a1n
p2 a21 a22 a2 n
pm am1 am 2 amn
pi вероятность применения игроком i ой стратегии
a11 p1 a21 p2 am1 pm v
a q a q a q v
1n n
11 1 12 2
Активной стратегией называется стратегия, входящая в
оптимальную смешанную стратегию с ненулевой вероятностью.
10.
Теорема 4 Если один из игроков придерживается своейоптимальной смешанной стратегии, то его выигрыш остается
неизменным и равен цене игры, не зависимо от того, какую
стратегию принимает второй игрок, если только тот не выходит за
пределы своих активных стратегий.
Пример:
4
2
2
10
B
1
3
5
7
9
5
3
12
15
B
2
6
B
3
10
7
25
A
1
A
2
A невыгодна
3
A
4
B
4
Стратегия Ak
игрока А называется доминирующей над
стратегией Al
, если ak , j al , j ( j 1, n) ,
а стратегия Al - доминируемой.
bi ,k bi ,l (i 1, n)
Bk - доминирующая над Bl , если
11.
Доминируемые стратегии можно убирать из матрицы игры, отэтого решение не изменится.
( ai , j ) m n (1)
(bai , j c) m n (2)
b, c 0
Теорема 5 Оптимальные смешанные стратегии p* и q*
в матричной игре (1) с ценой игры v будут оптимальными и в
матричной игре (2) с ценой v bv c.
12.
Пример исследования матричной игры4
2
A
7
8
7
3 4 5
6 8 10
5 3 7
5 6
13.
Решение матричной игры 2 2p1 a11
p2 a21
q1
a22
a12
q2
a11 p1 a21 p2 v
a12 p1 a22 p2 v
p2 1 p1
a11 p1 a21(1 p1) v
a12 p1 a22 (1 p1) v
p1(a11 a21) a21 v
p1(a12 a22 ) a22 v
p1(a11 a21) a21 p1(a12 a22 ) a22
p1(a11 a21) a21 v
a22 a21
p1
аналитический метод решения
a11 a21 a12 a22
Для q : a11q1 a12 (1 q1) v
i
14. Игры (геометрия) Статические игры
15.
Геометрический способ решения игры(2x2)V (a11 a21) p1 a21
V’
1 уравнение
a p a (1 p ) V
21
1
11 1
a p a (1 p ) V
22
1
12 1
V
2 уравнение
1
P1
P
Варианты решений:
V’
V’
V’
V’
V
V
P
P
V’
V
P
V’
V’
V
V
V
P
P
P
V
P
16.
Геометрическое решение игры (2xN) и (Mx2)0 0 q3 q4
2
4
2 3 1
3 2
6
p1
p2 1 p1
2 p 4(1 p ) V
1
1
2 p1 3(1 p1 ) V
3 p1 2(1 p1 ) V
p 6(1 p ) V
1
1
p1 2 7 p1 6
8 p1 4
1
1
p1* , p2*
2
2
V 2,5
2 p 4 V
1
p 3 V
1
p1 2 V
7 p 6 V
1
3q3 q4 2,5
3q3 1 q3 2,5
4q3 3,5
7
1
q3* , q*4
8
8
17.
Геометрическое решение игры (2xN) и (Mx2)3
5
A 4
2
6
5
7
1
4
3
Отв. P=(0; 0,6; 0; 0; 0,4); Q=(0,8; 0,2); V=5,4
18.
Приведение игры к ЗЛПm
aij pi V
i 1
m
pi 1,
i 1
p 0 (i 1,m)
i
p
x i
i V
m
aij xi 1
i 1
(i 1,m)
n
aij q j V
j 1
n
q j 1, q j 0 ( j 1,n)
j 1
q
y j
j V
n
aij y j 1
j 1
( j 1,n)
1
x x x min
1 2
m V
1
y y y max
1 2
m V
x 0 (i 1,m)
i
y 0 ( j 1,n)
j
19.
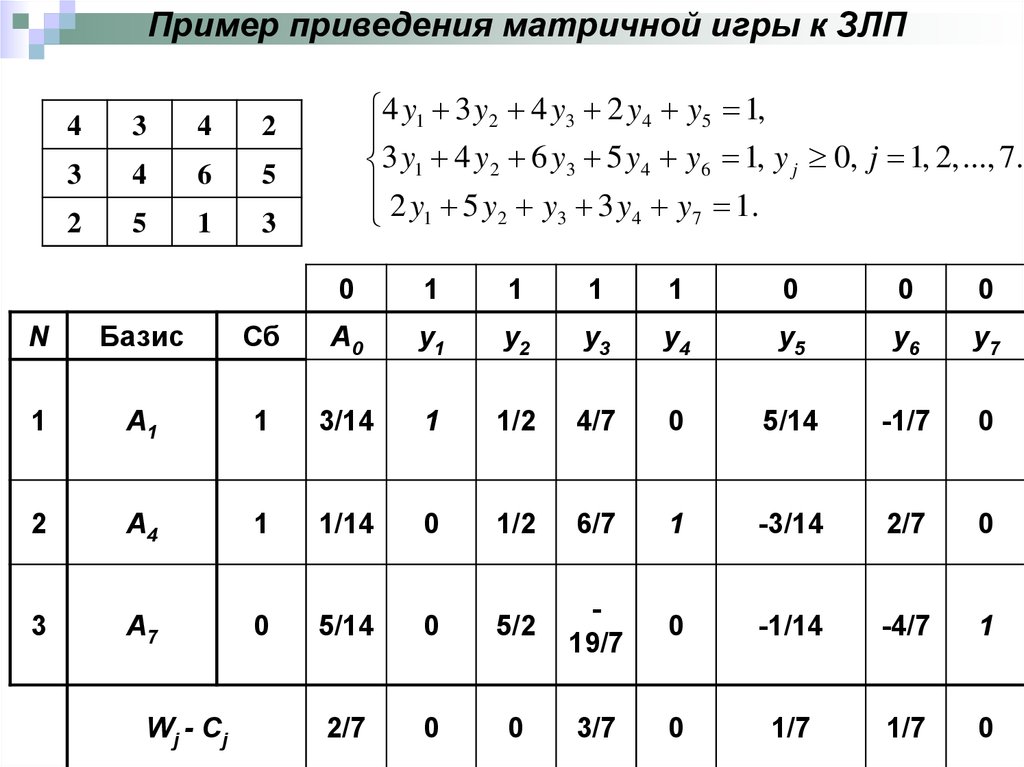
Пример приведения матричной игры к ЗЛП4
3
4
2
3
4
6
5
2
5
1
3
4 y1 3 y2 4 y3 2 y4 y5 1,
3 y1 4 y2 6 y3 5 y4 y6 1, y j 0, j 1, 2, ..., 7.
2 y 5 y y 3 y y 1.
2
3
4
7
1
0
1
1
1
1
0
0
0
N
Базис
Сб
A0
y1
y2
y3
y4
y5
y6
y7
1
A1
1
3/14
1
1/2
4/7
0
5/14
-1/7
0
2
A4
1
1/14
0
1/2
6/7
1
-3/14
2/7
0
3
A7
0
5/14
0
5/2
19/7
0
-1/14
-4/7
1
2/7
0
0
3/7
0
1/7
1/7
0
Wj - C j
20.
Статические игры (игры с “природой”)П ......................П поведение природы
1
n
A a11........................a1n
1
A a ........................a
2 21
2n
..................................
A a ..........................a
m m1
mn
q ...........................q
1
n
Существуют два класса игр с природой:
1. Первый класс, когда к каждому состоянию природы можно
приписать некоторую вероятность.
• Второй класс, когда к каждому состоянию природы не
можем приписать некоторую вероятность.
21.
Принципы и критерии для выбора решения1. Критерий Байеса
Оптимальной стратегией будет стратегия, в которой достигается
max a
i
n
a a q
i
ij j
j 1
2. Принцип недостаточного основания Лапласа
Если мы не знаем вероятности, то положим состояние природы
1
равновероятными:
q
j n
3. Максиминный критерий Вальда
min aij .
Оптимальна та стратегия, в которой лежит элемент max
j
i
Это пессимистический критерий (рассчитан на самый хороший
вариант в самом плохом случае).
22.
4. Критерий минимального риска Сэвиджаr a риск игрока А
ij
j ij
β max a
j
ij
(r )
матрица риска
ij mxn
Риск – плата за отсутствие информации.
Оптимальна та стратегия, в которой лежит минимальный из
максимальных рисков:
w min max r .
ij
i
j
23.
5. Критерий оптимизма – пессимизма Гурвицаmax[ min (a ) (1 ) max(a )], где 0 1
ij
ij
j
i
j
коэффициент оптимизма
1 крайний пессимизм критерий Вальда
0 крайний оптимизм
0,6
24.
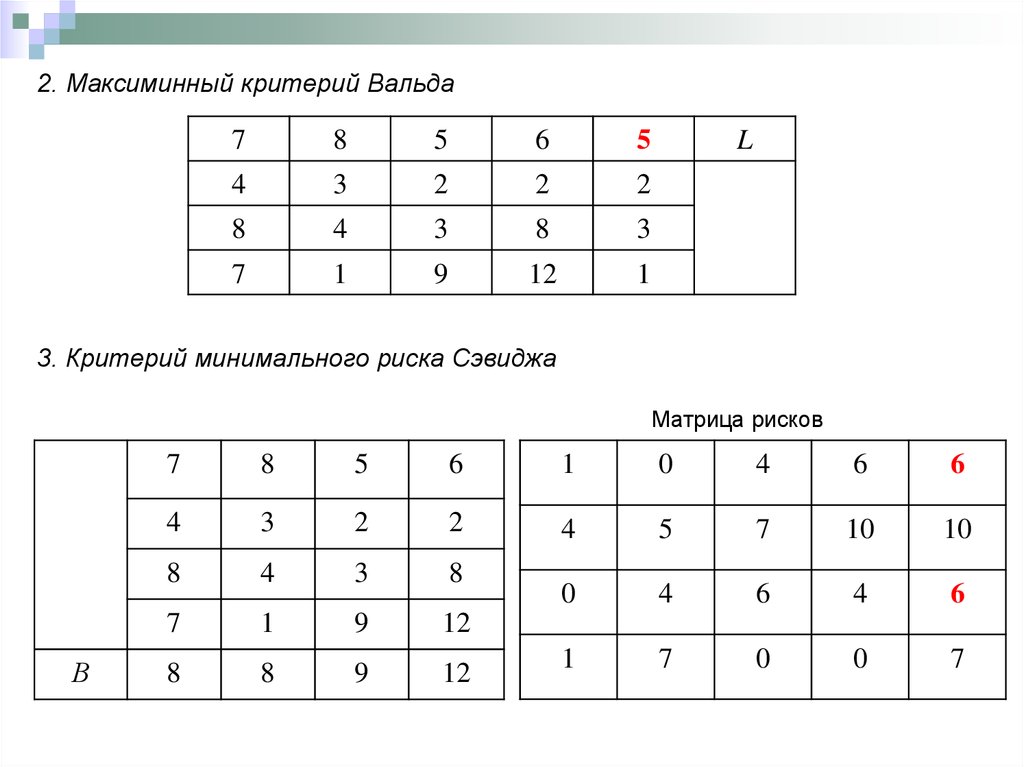
Пример:B1
B2
B3
B4
L
A1
7
8
5
6
5
A2
4
3
2
2
2
A3
8
4
3
8
3
A4
7
1
9
12
1
B
8
8
9
12
1. Критерий Байеса
P
7
8
5
6
6,65
4
3
2
2
2,8
8
4
3
8
5,8
7
1
9
12
6,85
0,25
0,3
0,2
0,25
25.
2. Максиминный критерий Вальда7
8
5
6
5
4
3
2
2
2
8
4
3
8
3
7
1
9
12
1
L
3. Критерий минимального риска Сэвиджа
Матрица рисков
В
7
8
5
6
1
0
4
6
6
4
3
2
2
4
5
7
10
10
8
4
3
8
0
4
6
4
6
7
1
9
12
8
8
9
12
1
7
0
0
7
26.
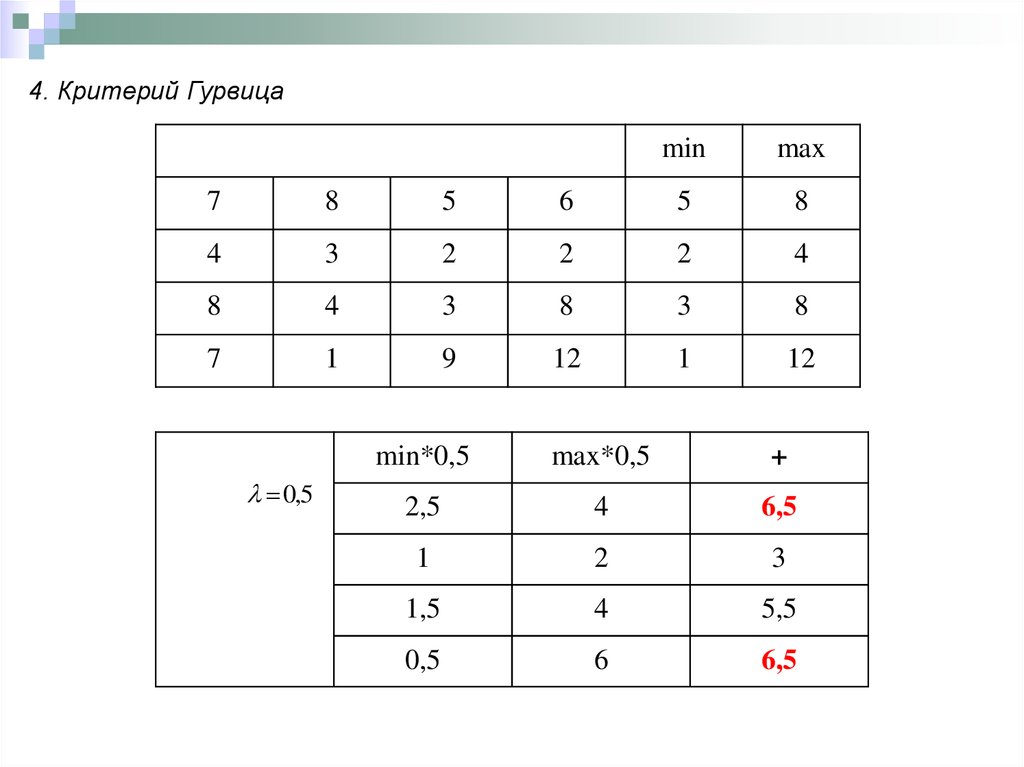
4. Критерий Гурвицаmin
max
7
8
5
6
5
8
4
3
2
2
2
4
8
4
3
8
3
8
7
1
9
12
1
12
0,5
min*0,5
max*0,5
+
2,5
4
6,5
1
2
3
1,5
4
5,5
0,5
6
6,5
27. Моделирование конфликтных ситуаций в экономике
Игры с природой28. Игры с природой
Определение. Игра, в которой осознанно действуеттолько один из игроков, называется игрой с
природой.
Природа может принимать одно из своих возможных
состояний и не имеет целью получение выигрыша.
Игра с природой представляется в виде платежной
матрицы, элементы которой – выигрыши игрока А, но
не являются проигрышами природы П.
Имеем. Игрок А, SА={p1,p2,…,pm}, FA(P,Пj)
Природа П с состояниями SП={п1,п2,…,пn}
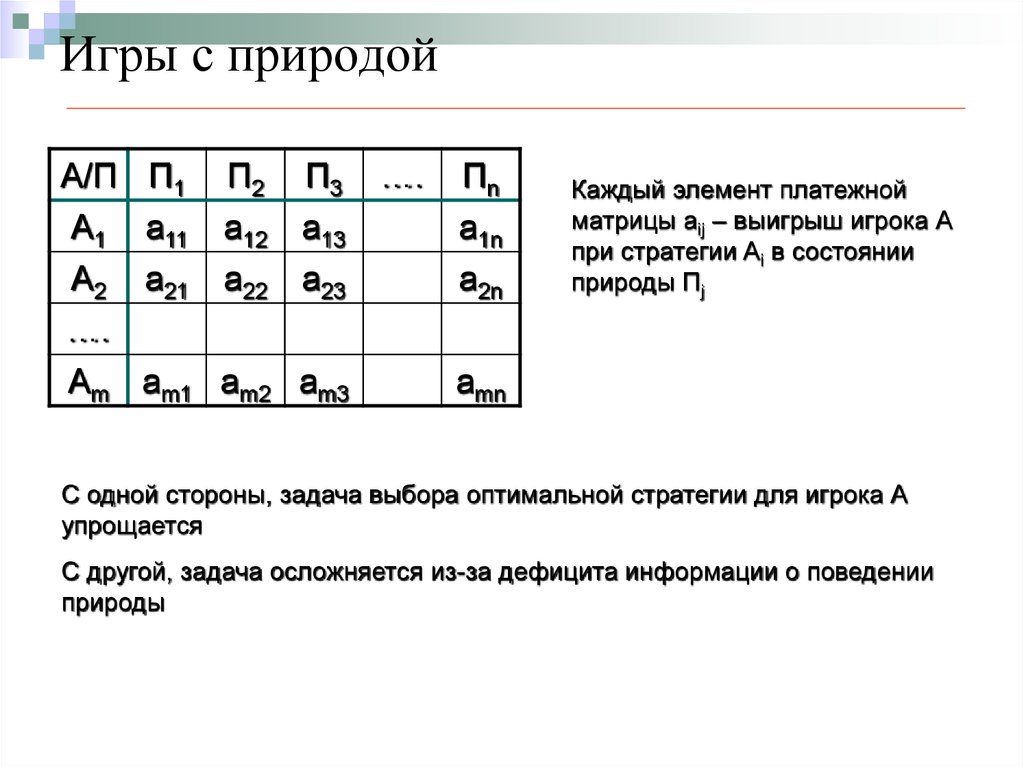
29. Игры с природой
A/ПA1
A2
….
Am
П 1 П 2 П3
a11 a12 a13
a21 a22 a23
am1 am2 am3
….
Пn
a1n
a2n
Каждый элемент платежной
матрицы aij – выигрыш игрока А
при стратегии Ai в состоянии
природы Пj
amn
С одной стороны, задача выбора оптимальной стратегии для игрока А
упрощается
С другой, задача осложняется из-за дефицита информации о поведении
природы
30. Игры с природой
Алгоритм решения задач остается прежним1. Анализируется наличие доминирующей стратегии игрока А. Если она
есть, то эта стратегия выбирается в качестве оптимальной
2. Производится редуцирование матрицы. При этом рассматриваются
только строки, т.к. «Природа» действует не осознанно
Замечание. Матрица выигрышей не всегда однозначно определяет выбор
оптимальной стратегии
На выбор стратегии оказывают влияние еще и показатели «удачности» или
«неудачности» выбора
Это условие называется «благоприятностью» природы
31. Игры с природой
Определение. Показателем благоприятностисостояния Пj природы П для увеличения выигрыша
называется наибольший выигрыш игрока А при этом
состоянии природы, т.е. наибольший элемент в j-ом
столбце платежной матрицы: βj=max(aij), j=1,2,…,n.
Для характеристики «удачности» применения игроком
стратегии Ai в состоянии природы Пj вводится
понятие риска.
Определение. Риском rij игрока А при выборе стратегии
Аi называется разность между показателем
благоприятности βj в состоянии природы Пj и
выигрышем аij: rij = βj-aij.
Риск – упущенная возможность получения
максимального выигрыша в данном состоянии
природы.
Из определения следует: rij ≥ 0.
32. Игры с природой
Определение. Верхняя граница рисков для каждогосостояния природы: wj=min(aij), j=1,2,…,n.
Или Wi –минимальный выигрыш при данном состоянии
природы
Колебание выигрыша в заданном состоянии природы:
Δrj=βj-wj.
Если aij= Wi – то риск является максимальным.
Следовательно по критерию риска эта стратегия
наихудшая
Если aij= βj (rjj=0), то стратегия Ai - безрисковая
Каждой платежной матрице игры можно поставить в
соответствие матрицу рисков.
Обратное не верно.
33. Игры с природой
Пример.Ai\Пj
П1
П2
П3
П4
П5
A1
9
4
5
1
3
A2
4
8
3
0
1
A3
4
βj
9
7
8
4
5
Матрица игры
8
8
2
3
Ai\Пj П1
П2
П3 П4 П5
A1
0
4
0
7
0
A2
5
0
2
8
2
A3
5
1
1
0
1
Матрица рисков
Если игрок выбирает стратегию А3, то игрок получает
одинаковый выигрыш при состояниях природы П1 и П3:
a31=a33=4
Однако, эти выигрыши не равноценны в смысле рисков, т.к.
удачность стратегии А3 к этим состояниям природы различно.
Благоприятность β1=9, а β3=5 соответственно риски r31=5, а
r33=1
34. Игры с природой
Пример. (Продолжение)Ai\Пj
П1
П2
П3
П4
П5
A1
9
4
5
1
3
A2
4
8
3
0
1
A3
4
βj
9
7
8
4
5
Матрица игры
8
8
2
3
Ai\Пj П1
П2
П3 П4 П5
A1
0
4
0
7
0
A2
5
0
2
8
2
A3
5
1
1
0
1
Матрица рисков
Может быть и другая ситуация. Выигрыши a21=a31=4 при этом
риски у стратегий при состоянии природы П1 одинаковы
r21=r31=5
Стратегии, у которых при одинаковых состояниях природы
равны риски, называются равноценными относительно этих
состояний природы
35. Игры с природой
Различают два вида задач в играх с природой:1. Задача о принятии решений в условиях риска, когда известны
вероятности, с которыми природа принимает каждое из возможных
состояний
2. Задачи о принятии решений в условиях неопределенности, когда нет
возможности получить информацию о вероятностях появления
состояний природы
36. Принятие решений в условиях риска
Пусть имеем игру с природой в условиях риска относительновыигрышей
A/П
П1
П2
П3 ….
Пn
A1
a11 a12 a13
a1n
A2
a21 a22 a23
a2n
….
Am
am1 am2 am3
qj
q1
q2
q3
amn
….
Игрок А имеет m возможных
чистых стратегий
Природа – n возможных
состояний
Каждое состояние появляется
с вероятностью qi
qn
Задача. Выбрать оптимальную стратегию поведения игрока А в
заданных условиях
В понятие оптимальности вкладываются различные соображения,
которые составляют содержание различных критериев
37. Критерий Бейса в принятии решений в условиях риска
Определение. Показателем эффективности чистой стратегии игрока –среднее значение выигрыша игрока при применении i-ой стратегии:
a
i
n
q a
j 1
j
ij
(8.1)
Определение. Оптимальной по Бейсу чистой стратегией игрока
относительно выигрышей считается такая стратегия, которая имеет
максимальный показатель эффективности (8.1)
a
0
i
max
a
i
n
max q aij
j
j
1
(8.2)
38. Критерий Бейса в принятии решений в условиях риска
Замечание. Стратегия, выбранная по критерию Бейса,является оптимальной не в каждом применении, а в среднем
Критерий Бейса можно распространить и на случай игры в
смешанных стратегиях
Пусть P={p1,p2,…,pm} смешанная стратегия игрока А, тогда
выигрыш игрока есть
H P,П p a
m
j
j
i 1
(8.3)
ij
i
Тогда показатель эффективности смешанной стратегии P есть:
n
n
m
m
n
m
H P q Hj P q p aij p q aij p a i
j 1
j
j 1
j
i 1
i
i 1
i
j 1
j
i 1
i
(8.4)
Показатель эффективности по Бейсу относительно выигрышей – среднее
взвешенное значение показателей эффективности чистых стратегий по тому
же критерию
39. Критерий Бейса в принятии решений в условиях риска
Определение. Пусть SA – множество всех стратегий игрока А.Оптимальной среди всех стратегий из множества SA – называется
стратегия Р0, показатель эффективности которой максимален:
max H P H P 0
Теорема. Стратегия Ai0 оптимальная среди всех чистых
стратегий игрока А по критерию Бейса относительно
выигрышей, является оптимальной по тому же критерию
критерию среди всех смешанных стратегий SA
Теорема говорит о том, что при принятии решения в условиях
риска по критерию Бейса относительно выигрышей, можно
обойтись только чистыми стратегиями
40. Критерий Бейса в принятии решений в условиях риска
Пример. Найти оптимальную стратегию предприятия при выпускепродукции, если платежная матрица имеет вид:
Ai\Пj П1
П2
П3
ai
A1 0.25 0.35 0.40 0.31
A2 0.70 0.20 0.30 0.47
A3
A4
qj
0.35 0.85 0.20 0.47
0.80 0.10 0.35 0.50
0.5 0.3 0.2
а1= 0.5*0.25+0.3*0.35+0.2*0.4=0.31
Для удобства решения задач
платежная матрица дополняется
столбцом ai и строкой qi
Оптимальной стратегией
предприятия по критерию Бейса
относительно выигрышей
является А4
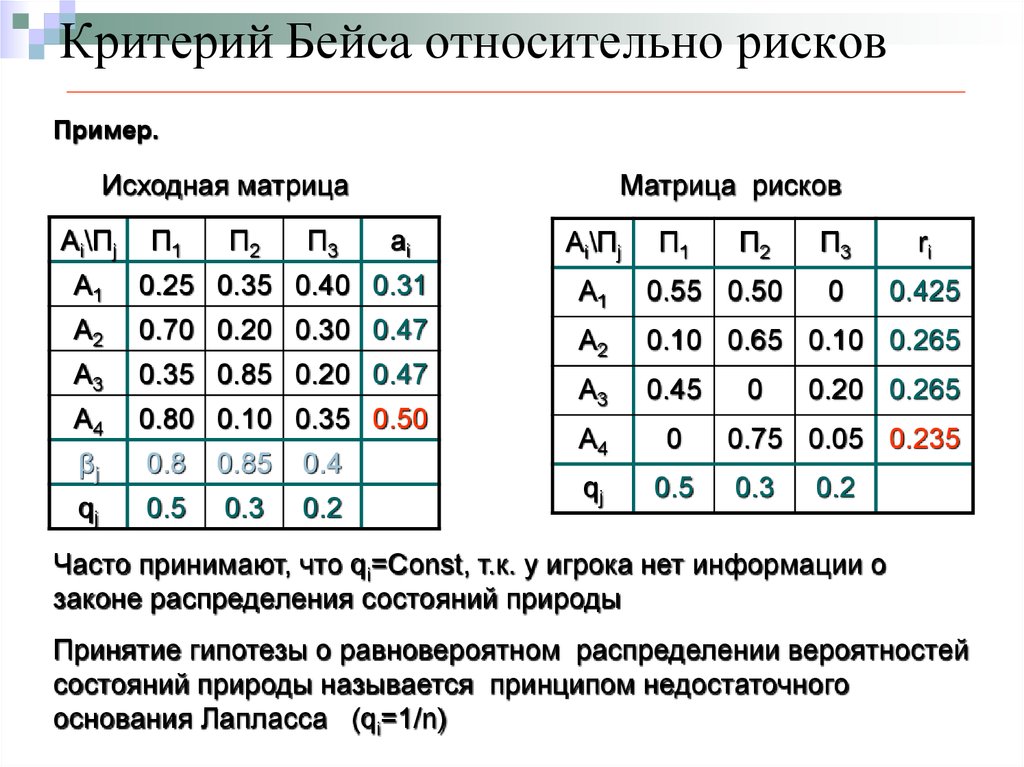
41. Критерий Бейса относительно рисков
Пусть имеем игру относительно рисков в условиях рискаA/П
A1
A2
….
Am
qj
П1
r11
r21
….
rm1
q1
П2
r12
r22
….
rm2
q2
П3
r13
r23
….
rm3
q3
…. Пn
…. r1n
…. r2n
…. ….
…. rmn
…. qn
Определение. Показателем
неэффективности стратегии
Ai по критерию Бейса
относительно рисков
называется средне
взвешенное значение риска в
i-ой строке:
n
r
i
q
j 1
j
r
ij
при
i 1,2,..., m
Определение. Оптимальной по критерию Бейса в игре
относительно рисков является стратегия Ai, показатель
неэффективности которой минимальный
r
0
i
min r i
42. Критерий Бейса относительно рисков
Риск смешанной стратегии P={p1,p2,…,pm}, принадлежащеймножеству SA, при состоянии природы ПJ, определяется как:
r j ( P , П j ) max H U ,П j H P , П j , при j 1,2,..., n
U s A
Показатель неэффективности смешанной стратегии
P{p1,p2,…pm}, принадлежащей множеству SA, относительно
рисков определяется как средне взвешенное рисков по строке
Оптимальной среди всех смешанных стратегий по критерию
Бейса относительно рисков считается та стратегия, для
которой показатель неэффективности имеет минимальное
значение
Теорема. Если стратегия Ai0 – оптимальная по критерию Бейса
относительно рисков среди всех чистых стратегий, то она
является оптимальной по тому же критерию среди всех
смешанных стратегий
43. Критерий Бейса относительно рисков
Пример.Исходная матрица
Ai\Пj
П1
П2
П3
Матрица рисков
ai
Ai\Пj
П1
П2
П3
ri
0
0.425
A1
0.25 0.35 0.40 0.31
A1
0.55 0.50
A2
0.70 0.20 0.30 0.47
A2
0.10 0.65 0.10 0.265
A3
0.35 0.85 0.20 0.47
0.45
A4
0.80 0.10 0.35 0.50
A3
βj
0.8
0.85
0.4
A4
0
qj
0.5
0.3
0.2
qj
0.5
0
0.20 0.265
0.75 0.05 0.235
0.3
0.2
Часто принимают, что qi=Const, т.к. у игрока нет информации о
законе распределения состояний природы
Принятие гипотезы о равновероятном распределении вероятностей
состояний природы называется принципом недостаточного
основания Лапласса (qi=1/n)
44. Принятие решения в условиях неопределенности
Особенность задачи – отсутствие информации о вероятностяхпоявления состояний природы
Для решения задачи Гурвиц предложил следующий подход
От платежной матрицы перейти к вспомогательной, которая
формируется из платежной матрицы путем сортировки
элементов каждой строки по возрастанию
Вспомогательную матрицу будем обозначать как В
В этой матрице в 1-ом столбце сгруппированы элементы с
минимальными выигрышами при всех стратегиях игрока и
всех состояниях природы
В последнем столбце наоборот содержатся максимальные
выигрыши при всех стратегиях и состояниях природы
45. Принятие решения в условиях неопределенности
Для учета возможности появления выигрышей вводится наборкоэффициентов λ1, λ2, …,λn, которые обладают свойством λ1+ λ2+ …+λn=1
Величина:
n
Gi л1 , л2 ,..., лn лj bij
(8.5)
j 1
называется показателем эффективности стратегии Ai по Гурвицу
Величина (8.5) учитывает все выигрыши возможные при i – ой стратегии и
зависит от значений коэффициентов λ1, λ2, …,λn, которые выступают в
качестве весов вклада каждой стратегии в показатель эффективности
46. Принятие решения в условиях неопределенности
Определение. Обобщенным критерием пессимизма-оптимизма Гурвица скоэффициентами λ1, λ2, …,λn относительно выигрышей называется критерий,
по которому оптимальной среди чистых стратегий является стратегия Ai с
максимальным показателем эффективности (8.5)
Числа
л
p
n
2
л
j 1
j
л
o
n
л
n
j 1
2
j
называются показателями пессимизма и оптимизма соответственно
Коэффициенты λ1, λ2, …,λn выбираются субъективно
47. Критерий Вальда (критерий крайнего пессимизма)
Критерий Вальда является частным случаем обобщенного критерияГурвица относительно выигрышей со специальными значениями
коэффициентов: λ1=1, λ2=λ3=…=λn=0
Подставляя значения коэффициентов в показатель эффективности (8.5)
получим:
W i Gi 1,0,0,..., 0 bi 1 mina ij
при i 1,2,..., m
(8.6)
1 j n
Wi представляет собой минимальный выигрыш при каждой стратегии, а
оптимальной считается стратегия с максимальным значением показателя
эффективности Wi
48. Критерий Вальда (критерий крайнего пессимизма
Другими словами, оптимальной среди чистых стратегий по критериюВальда считается та чистая стратегия, при которой минимальный выигрыш
является максимальным среди минимальных выигрышей всех чистых
стратегий.
По критерию Вальда показатель пессимизма λр=1, а показатель оптимизма
λо=0
Критерий Вальда ориентирует игрока на неблагоприятные для него
состояния природы
Отсюда название «Критерий крайнего пессимизма»
49. Критерий крайнего оптимизма
Данный критерий является противоположностью критерия ВальдаПредполагается, что λ1=λ2=…=λn-1=0, λn=1, тогда
M G 0,0,..., 0,1 b
i
i
in
max aij
при i 1,2,..., m
1 j n
Оптимальной среди чистых стратегий по критерию максимального
оптимизма будет стратегия A0, для которой справедливо условие:
M max M i max
1 i m
В этом случае λр=0, λо=1
1 i m
max aij
1 j n
50. Критерий пессимизма-оптимизма Гурвица
Данный критерий является некоторым обобщением критериев крайнегопессимизма и крайнего оптимизма и также представляет собой частный
случай обобщенного критерия Гурвица относительно выигрышей при
следующем допущении:
λ1=1-λ, λ2=λ3=…=λn-1=0, λn=λ,
где 0≤λ≤1
Тогда показатель эффективности стратегии Ai по Гурвицу есть:
G G 1 л,0,0,..., л 1 л b
i
i
i1
лbin 1 л min aij лmax aij
1 j n
(8.7)
1 j n
Оптимальной стратегией Ai0 считается стратегия с максимальным
значением показателя эффективности (8.7)
51. Критерий пессимизма-оптимизма Гурвица
Показатели пессимизма и оптимизма при этом равны соответственноλp=1-λ, λo=λ
Показатель эффективности (8.7) соответствует показателю эффективности
крайнего пессимизма при λ=0 и крайнего оптимизма при λ=1
При λ=0.5 (реалистичная ситуация) λp=0.5, λo=0.5
Замечание. Рассмотренные критерии не учитывают всех возможных
состояний природы. Принятие решения производится на основании только
крайних значений выигрыша
Только обобщенный критерий Гурвица позволяет учесть весь спектр
возможных выигрышей!
52. Обобщенный критерий Гурвица относительно выигрышей
Т.к. в матрице В все элементы по строкам упорядочены в порядкевозрастания, это свойство положено в основу определения значений
неизвестных коэффициентов λj
Введем следующие обозначения:
b b
Сумма выигрышей по j-ому столбцу
матрицы В
1 m
b
j
bj m
i 1
Среднее значение выигрыша по J-ому
столбцу матрицы В
m
j
i 1
ij
n
n
m
j 1
j 1 i 1
b1≤b2≤…≤bn
и
b b j aij
Общая сумма выигрышей по всей
матрице
b1≤b2≤…≤bn
53. Обобщенный критерий Гурвица относительно выигрышей
Игроку предлагаются два подхода к выбору оптимальной стратегии:- более осторожный, при котором коэффициенты λ убывают с
ростом средних значений выигрышей по столбцам
- более оптимистичный, при котором значения коэффициентов λ
возрастают с ростом средних значений выигрышей по столбцам
Выбор подхода (оценка реальной ситуации опасная/безопасная)
возлагается на игрока
54. Обобщенный критерий Гурвица относительно выигрышей
Безопасная ситуация (оптимистичный подход)λ1:λ2:λ3:…:λn = b1:b2:b3:…:bn
л
j
bj
b
(8.8)
Опасная ситуация (пессимистический подход)
λ1:λ2:λ3:…:λn = bn:bn-1:bn-2:…:b1
л
j
b n j 1
b
(8.9)
55. Пример игры с природой
Задача. «Покупка акций»Пусть инвестор может купить акции трех компаний К1, К2 и К3,
руководствуясь показателем доходности акций.
Ситуация на фондовом рынке меняется со временем, что сказывается на
показателях доходности
Тогда в качестве игрока можно принять инвестора, а в качестве природы –
ситуацию на рынке в различные моменты времени
Пусть известны показатели доходности акций за 4-ре последовательных
месяца «январь» - «апрель»
Вопрос. Какие акции целесообразно купить акционеру?
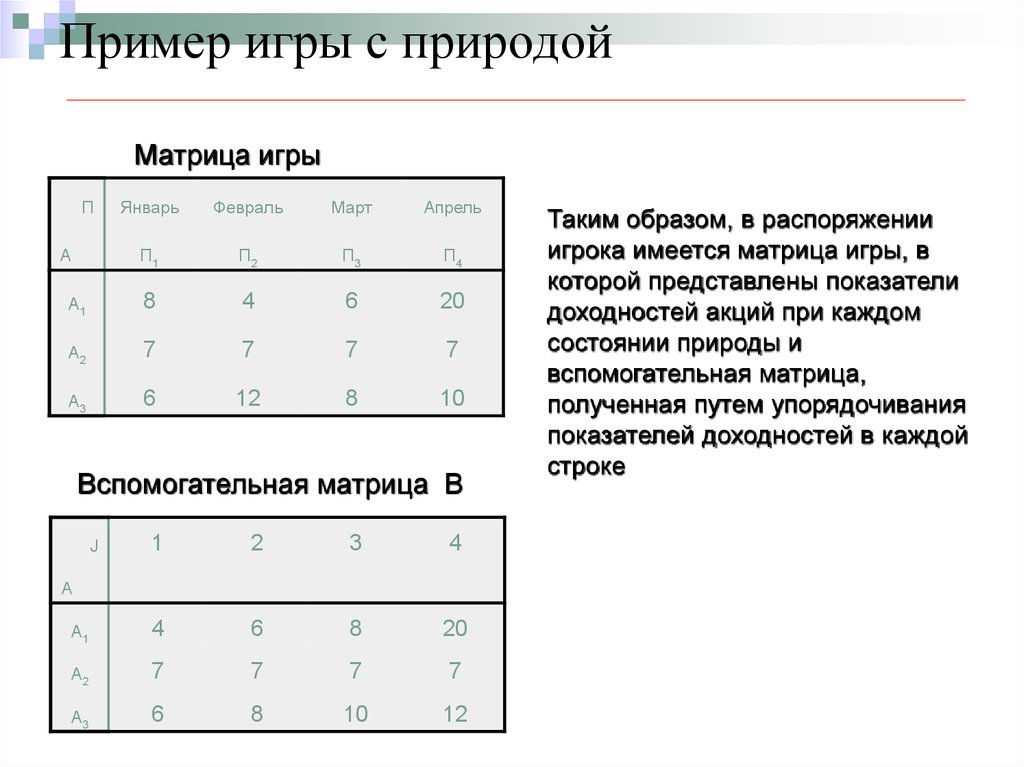
56. Пример игры с природой
Матрица игрыП
Январь
Февраль
Март
Апрель
П1
П2
П3
П4
А1
8
4
6
20
А2
7
7
7
7
А3
6
12
8
10
А
Вспомогательная матрица В
1
2
3
4
А1
4
6
8
20
А2
7
7
7
7
А3
6
8
10
12
J
А
Таким образом, в распоряжении
игрока имеется матрица игры, в
которой представлены показатели
доходностей акций при каждом
состоянии природы и
вспомогательная матрица,
полученная путем упорядочивания
показателей доходностей в каждой
строке
57. Пример игры с природой
J1
2
3
4
Wi
Mi
Gi(опт)
Gi(пес)
А1
4
6
8
20
4
20
8.86
15.4
А2
7
7
7
7
7
7
7.00
7.00
А3
6
8
10
12
6
12
7.82
10.18
А
Bj
17 21
25
Стратегии оптимальные с
позиций критериев Вальда и
крайнего оптимизма
находятся очень просто
Найдем оптимальные
стратегии по критерию
пессимизма – оптимизма
Гурвица
39
Подход пессимиста. λ выбирается из условия невозрастания
среднего:
л л
4
b
1
b1 b4
17
17
0.304
17 39 56
л 1 0.304 0.696
1
G1(λ)=λ1*W1+λ4*M1=0.696*4+0.304*20=8.86
G2(λ)=0.696*7+0.304*7=7;
G3(λ)=0.696*6+0.304*0.696=7.82
Подход оптимиста. λ выбирается из условия неубывания среднего
λ=λ1=b4/(b1+b4)=0.696
λ4=(1-λ)=0.304
58. Пример игры с природой
12
3
4
G
1
4
6
8
20
7.98
11.5
2
7
7
7
7
7.00
7.00
3
6
8
10
12
8.31
9.69
17
39
102
17
102
21
25
102
21
102
25
21
102
25
102
39
17
102
39
102
A
J
A
A
A
b
j
пес
опт
пес
G
опт
Найдем оптимальные стратегии по
обобщенному критерию Гурвица
Опасная ситуация. Коэффициенты λ
вычисляются по (8.9)
b=17+21+39=102
λ1=39/109; λ2=25/102; λ3=21/102; λ4=17/102
Показатели эффективности по Гурвицу по (8.5)
пес
G
1
пес
G
2
пес
G
3
4
39
25
21
17
6
8
20
7.98
102
102
102
102
7
39
25
21
17
7
7
7
7.00
102
102
102
102
6
39
25
21
17
8
10
12
8.31
102
102
102
102




















































 mathematics
mathematics








