Тригонометрические функции

1.

Презентация на тему:
«Тригонометрические функции»
900igr.net

2.

Числовая окружность
В
I
II
А
С
IV
III
D

3.

Синус, косинус, тангенс и котангенс
Знаки по четвертям:
Если M (t) = M (x; y), то
y
x cos t ,
y sin t
1 sin t 1 1 cos t 1
1
+
–1
+
+
–
–
–
–
–1
sin t
tgt
, t k,
cos t
2
cos t
ctgt
, t k,
sin t
sin t
cost
1
x
+
M(t)=M(x;y)
tgt , ctgt
y
–
+
+
–
x

4.

Значения тригонометрических функций
30 45 60
6
4
90
2
3
180 3 270
2
sin
1
2
2
2
3
2
1
0
–1
cos
3
2
2
2
1
2
0
–1
0
tg
1
3
1
3
–
0
–
1
1
3
0
–
0
ctg
3

5.

Свойства синуса, косинуса, тангенса и котангенса
cos( t ) cos t ,
sin(t 2 k ) sin t ,
sin( t ) sin t ,
cos(t 2 k ) cos t ,
tg ( t ) tgt ,
tg (t ) tgt ,
ctg ( t ) ctgt .
ctg (t ) ctgt .
sin t cos t ,
2
cos t sin t .
2
sin( t ) sin t ,
cos( t ) cos t ,
у
t
2
t t
0
х
3
2
у
2
t
2
3
2
0
х

6.

Основные тригонометрические формулы
sin t cos t 1, sin t 1 cos t ,
2
2
cos t 1 sin t.
2
2
2
sin t
tgt
, t k, k Z
cos t
2
cos t
ctgt
, t k, k Z
sin t
1
1 tg t
, t k, k Z
2
cos t
2
2
1
1 ctg t
, t k, k Z
2
sin t
2
2

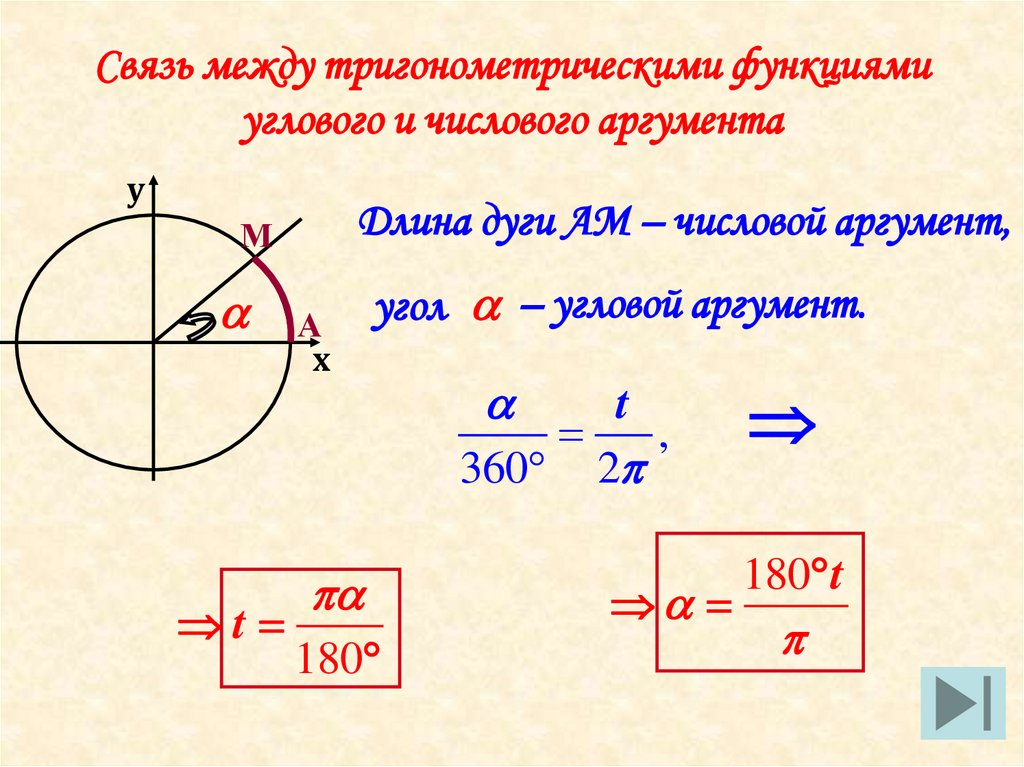
7. Связь между тригонометрическими функциями углового и числового аргумента

у
Длина дуги АМ – числовой аргумент,
М
А
х
угол – угловой аргумент.
t
,
360 2
t
180
180 t

8.

Угол в 1 рад – это центральный угол ,
длина дуги которого равна радиусу
окружности.
Таким образом, в тригонометрии
независимую переменную мы можем считать
числовым аргументом или угловым
аргументом.