Регрессио́нный анализ. Примеры применения регрессионного анализа

1. Регрессио́нный анализ. Примеры применения регрессионного анализа.

Регрессио́ нный анализ.
Примеры применения регрессионного
анализа.
• Моделирование потоков миграции в зависимости от
таких факторов как средний уровень зарплат, наличие
медицинских, школьных учреждений, географическое
положение и др.
• Моделирование дорожных аварий как функции
скорости, дорожных условий, погоды и т.д.
• Моделирование потерь от пожаров как функции от
таких переменных как количество пожарных станций,
время обработки вызова, или цена собственности.
Суть регрессионного анализа заключается в
нахождении наиболее важных факторов,
которые влияют на зависимую переменную!

2.

Регрессионный анализ используют
для решения задач:
• Установления формы зависимости между
переменными (линейная-нелинейная,
отрицательная-положительная и т.д.).
• Определения функции регрессии.
Важно выяснить, каково было бы действие на
зависимую переменную главных факторов, если
бы прочие факторы не изменялись и если бы
были исключены случайные элементы.
Цель регрессионного анализа - по значениям одной
переменной, выбранной в качестве аргумента,
предсказать соответствующее значение другой
(функции).

3. Регрессио́нный анализ

Регрессио́ нный анализ
Регрессио́ нный анализ - статистический метод
исследования влияния одной или нескольких независимых
переменных X1,X2,...,Xi на зависимую переменную Y.
Уравнение регрессии - это математическая формула,
применяемая к независимым переменным, чтобы лучше
спрогнозировать зависимую переменную, которую
необходимо смоделировать
y = f (x1, x2, …, xi) + ε
f - заранее не известная функция, подлежащая определению;
ε - ошибка аппроксимации данных.
Уравнение множественной линейной регрессии
y = а0 + b1x1 + b2x2, … + bixi

4. Измерение экспериментальных данных

Зависимая переменная (Y) - это переменная,
описывающая процесс, который мы пытаемся
предсказать или понять.
Независимые переменные (X) это переменные,
используемые для моделирования или
прогнозирования значений зависимых
переменных.
Существует необъяснимое количество зависимых
величин, представленных в уравнении регрессии
как случайные ошибки ε.

5. Линейная регрессия

В линейной регрессионной модели функция имеет
вид
f (xi) = a+bxi
А сама модель имеет следующий вид:
yi=a + bxi
При данных а и b сумма квадратов
отклонений экспериментальных данных от
найденной прямой будет наименьшей.

6.

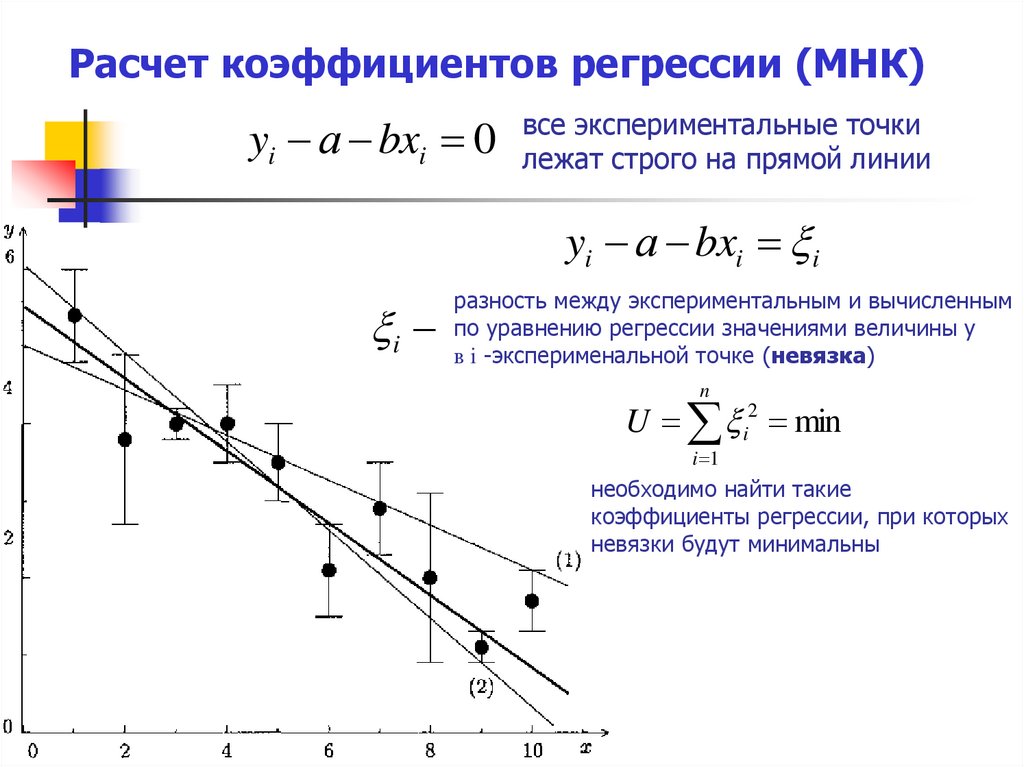
Расчет коэффициентов регрессии (МНК)
yi а bxi 0
все экспериментальные точки
лежат строго на прямой линии
yi а bxi i
i
разность между экспериментальным и вычисленным
по уравнению регрессии значениями величины у
в i -эксперименальной точке (невязка)
n
U i2 min
i 1
необходимо найти такие
коэффициенты регрессии, при которых
невязки будут минимальны

7.

Расчет коэффициентов регрессии (МНК)
n
n
i 1
i 1
U i2 ( yi а bxi ) 2 min
n
dU
2 ( yi а bxi ) 0
dа
i 1
n
dU
2 ( yi а bxi ) xi 0
db
i 1
а
n
n
n
n
i 1
i 1
i 1
i 1
2
2
y
x
i i yi xi xi
n x xi
i 1
i 1
n
n
2
i
n
n
i 1
i 1
nа b xi yi
n
n
n
а xi b x yi xi
i 1
b
2
i
i 1
i 1
n
n
n
i 1
i 1
i 1
n yi xi yi xi
n x xi
i 1
i 1
n
n
2
i
2

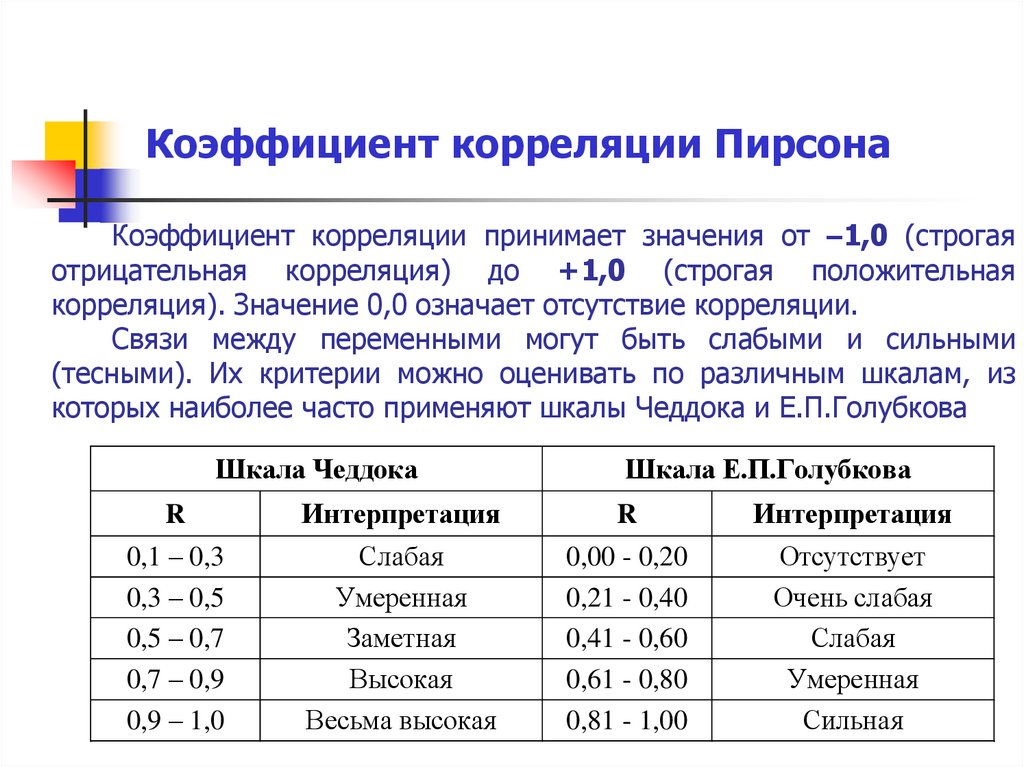
8. Коэффициент корреляции Пирсона

n
R
cov x, y
x y
x
i 1
n
i
x yi y
n
2
x
x
y
y
i
i
i 1
2
i 1
Условия применения коэффициента корреляции
Пирсона:
1. Переменные x и y должны быть распределены нормально.
2. Переменные x и y должны быть измерены в интервальной
шкале или шкале отношений.
3. Количество значений в исследуемых переменных x и y
должно быть одинаковым.
Значение коэффициента корреляции не зависит от масштаба

9. Коэффициент корреляции Пирсона

Коэффициент корреляции принимает значения от –1,0 (строгая
отрицательная корреляция) до +1,0 (строгая положительная
корреляция). Значение 0,0 означает отсутствие корреляции.
Связи между переменными могут быть слабыми и сильными
(тесными). Их критерии можно оценивать по различным шкалам, из
которых наиболее часто применяют шкалы Чеддока и Е.П.Голубкова
Шкала Чеддока
Шкала Е.П.Голубкова
R
Интерпретация
R
Интерпретация
0,1 – 0,3
0,3 – 0,5
0,5 – 0,7
0,7 – 0,9
0,9 – 1,0
Слабая
Умеренная
Заметная
Высокая
Весьма высокая
0,00 - 0,20
0,21 - 0,40
0,41 - 0,60
0,61 - 0,80
0,81 - 1,00
Отсутствует
Очень слабая
Слабая
Умеренная
Сильная

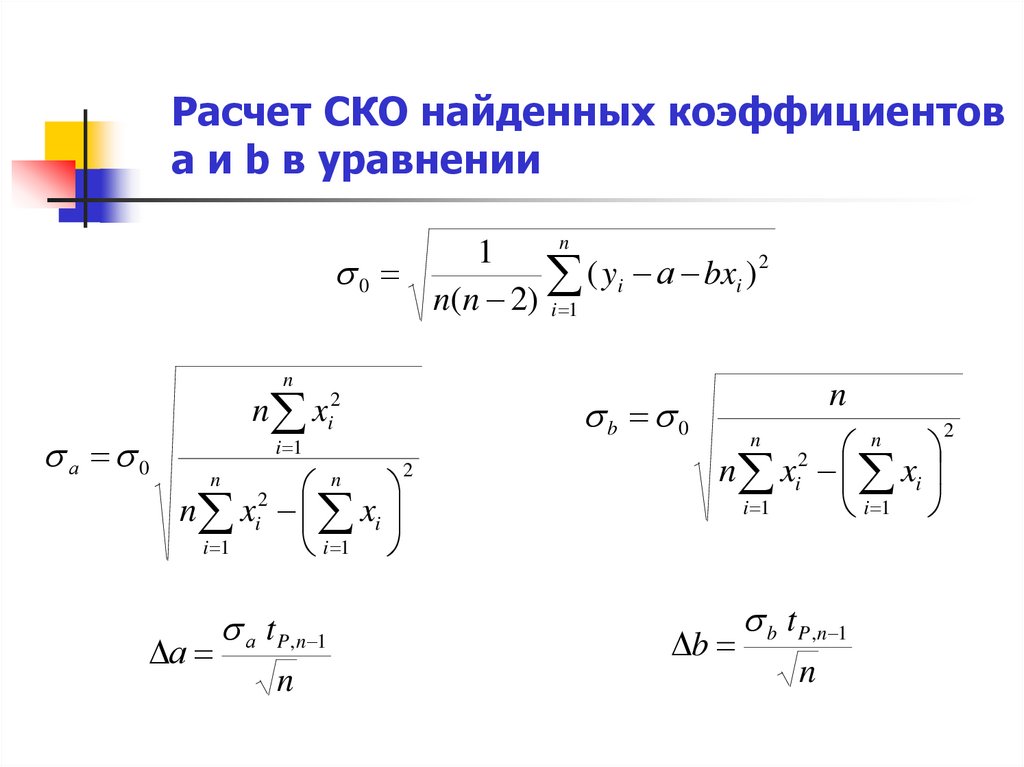
10. Расчет СКО найденных коэффициентов а и b в уравнении

n
1
2
0
(
y
а
bx
)
i
i
n(n 2) i 1
n
а 0
n xi2
b 0
i 1
n
n x xi
i 1
i 1
n
2
i
а
а t P ,n 1
n
2
n
n x xi
i 1
i 1
n
n
2
i
b
b t P ,n 1
n
2

11. Анализ нелинейных зависимостей. Линеаризация зависимостей

Замены
Вид зависимости
Парабола второго (или высшего)
порядка
y ax 2 b
a
y
b
Гипербола
x
Логарифмическая функция
y a ln x b
Показательная функция
Степенная функция
y ba
y bx a
Экспоненциальная функция
x
y
ax b
x
y be ax
Ограничения
u
k
z
y
x2
a
b
y
1
x
a
b
x 0
y
ln x
a
b
x>0
ln y
x
ln a
ln b
ln y
ln x
a
ln b
ln y
x
a
ln b
1
x
a
b
1
y
y>0
a>0
b>0
y>0
x>0
b>0
y>0
b>0
y 0
x 0