Similar presentations:
Векторное произведение векторов
1. Векторное произведение векторов
• Векторным произведениемвекторов а и b называется
вектор с , обозначаемый c a b,
который удовлетворяет
следующим трём условиям:
2.
• 1. с | a b | a b sin ;• 2. c à, c b ,
• 3. тройка a , b , c – правая (т.е.
при наблюдении
из
конца
вектора с кратчайший
поворот от а к b виден
совершающимся против
часовой стрелки.
3.
4. Свойства векторного произведения
ab
(
b
a
)
• 1.
b (a b )
• 2. ( a )
c
• 3. a ( b c ) a b a
• 4. a b 0 a || b
5.
• Если a x1 , y1 , z1b x2 , y2 , z2
то векторное произведение
вычисляется по формуле
i
a b x1
j
y1
k
z1
x2
y2
z2
6. Приложения векторного произведения к задачам геометрии и механики.
7.
Площадь параллелограмма
(геометрический смысл
векторного произведения).
S | a || b | sin | a b |
Площадь треугольника
1
S | a b |
2
8.
Момент силы (механический
смысл векторного
произведения).
Пусть точка А твердого тела
закреплена, а в точке
В
приложена сила F . Тогда
возникает вращающий момент
M AB F
9.
• Пример. Вычислить площадьтреугольника с вершинами
A(7,3,4), B(1,0,6) , C(4,5,-2).
10.
• Решение. Находим векторыAB ( 6, 3, 2), AC ( 3, 2, 6).
• Вычисляем векторное
произведение
11.
k2
i
j
AB AC 6 3
3
3 2
i
j
2 6
k
6 3
3
2
2
6
6
2
3
6
12.
14i 42 j 21k .• Тогда
1
1
2
2
2
S | AB AC |
14 42 21
2
2
1
49
2
2
2
7 2 6 3
24,5.
2
2
13. Смешанное произведение векторов
• Определение. Смешаннымпроизведением
трех
векторов
a , b , c называется число
a b c (a b ) c
14.
• Еслиa x1 , y1 , z1 , b x2 , y 2 , z 2 ,
с x3 , y3 , z3
• то
x1
а b с x2
x3
y1
z1
y2
y3
z2
z3
15. Приложения смешанного произведения к задачам геометрии
16.
Объём параллелепипеда,
построенного
на векторах
a , b , c (геометрический смысл
смешанного произведения).
V | a b c |
Объём пирамиды
1
V |ab c |
6
17.
Условие компланарности
векторов в координатной
форме:
– компланарны
a, b , c
x1
a b c 0 x2
y1
y2
z1
z 2 0.
x3
y3
z3
18.
• Пример. Вычислить объёмпирамиды с вершинами в
точках A(2,0,0), B(0,3,0), C(4,0,6),
D(2,3,8).
19.
• Решение. Находим векторыAB ( 2, 3, 0)
AC (2, 0, 6)
AD (0, 3, 8)
Вычислим смешанное
произведение этих векторов:
20.
2 3 0AB AC AD
2 0 6
0
2
0 6
3 8
3
3 8
2 6
0 8
0 2(0 18)
3(16 0) 36 48 12
21.
• Тогда1
| 12 |
V | AB AC AD |
2.
6
6
22.
23. Модуль 2
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ24. Плоскость и её основные уравнения
• Рассмотрим плоскость P впрямоугольной декартовой
системе координат.
25.
• Положение плоскости вполнеопределяется
точкой
M 0 ( x0 , y 0 , z 0 ) P
и вектором нормали
n ( A, B, C ) P (n 0)
26.
27.
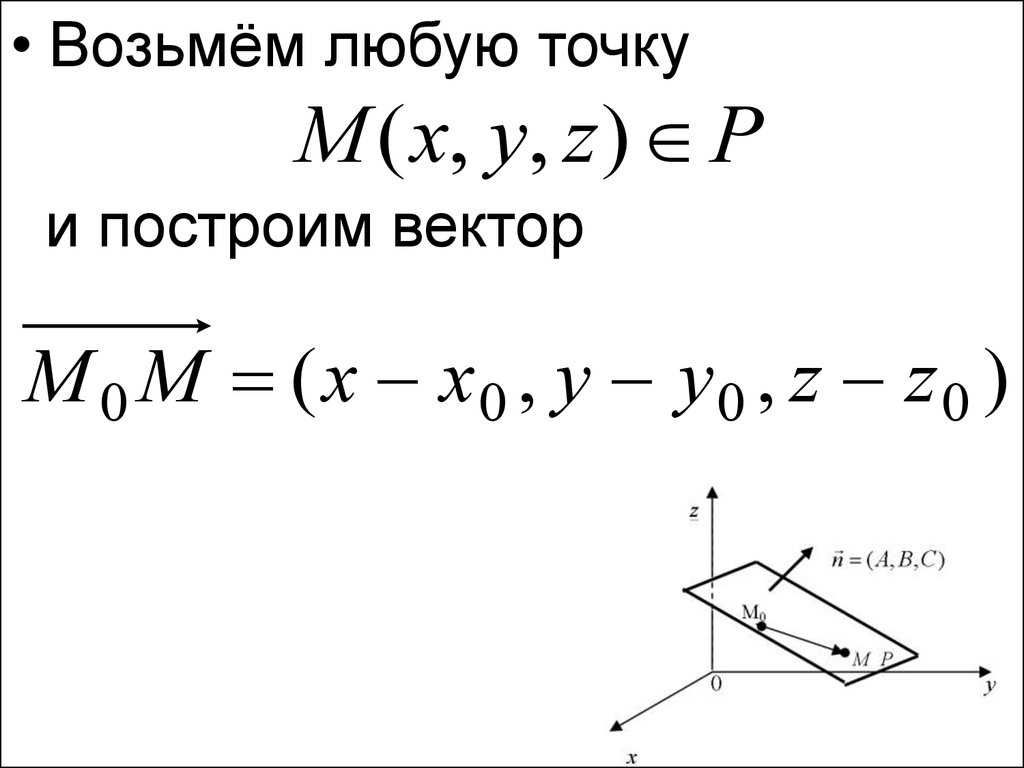
• Возьмём любую точкуM ( x, y, z ) P
и построим вектор
M 0 M ( x x0 , y y 0 , z z 0 )
28.
• Так как n M 0 M , то скалярноепроизведение
или
n M 0 M 0,
A( x x0 ) B( y y 0 ) C ( z z 0 ) 0.
29.
• Получили уравнение плоскости,заданной
точкой M 0 ( x0 , y 0 , z 0 )
и вектором нормали n ( A, B, C )
30.
• Если в уравненииA( x x0 ) B( y y0 ) C ( z z0 ) 0
раскрыть скобки и обозначить
D Ax0 By 0 Cz 0
то получим общее уравнение
плоскости:
Ax By Cz D 0
( A B C 0)
2
2
2
31.
• Теорема. Всякое уравнениевида
Ax By Cz D 0
( A B C 0)
2
2
2
определяет некоторую
плоскость в пространстве.
32.
• Если в этом уравнении какойлибо из коэффициентов A, B, Cравен нулю, то плоскость
расположена параллельно той
оси, координата которой
отсутствует в уравнении.
33.
• Например, при A = 0 плоскостьBy + Cz + D = 0 параллельна оси
Ox; при A = B = 0 плоскость Cz +
D = 0 параллельна осям Ox и
Oy, т.е. плоскости xOy и т.д.
34.
• Пусть в уравненииAx By Cz D 0
ни один из коэффициентов не
равен 0. Перепишем это
уравнение в виде
Ax By Cz D
разделим обе части этого
равенства на - D и обозначим
35.
DD
D
a, b, c
A
B
C
Получим уравнение плоскости в
отрезках:
x y z
1,
a b c
36.
• где a, b, c – это величинынаправленных отрезков,
отсекаемых плоскостью на осях
координат
37.
38.
• Если три точкиM 1 ( x1 , y1 , z1 )
M 2 ( x2 , y 2 , z 2 )
M 3 ( x3 , y 3 , z 3 )
не лежат на одной прямой, то
через эти точки проходит
единственная плоскость:
39.
40.
• Уравнение плоскости,проходящей через три точки,
имеет вид:
x x1
y y1
z z1
x 2 x1
y 2 y1
z 2 z1 0.
x3 x1
y 3 y1
z 3 z1
41.
• Пусть даны двеP1 : A1 x B1 y C1 z D1 0
и
P2 : A2 x B2 y C2 z D2 0
• Угол φ между двумя
плоскостями
равен углу между
их векторами
нормали:
42.
cosn1 n2
n1 n2
A1 A2 B1 B2 C1C2
A B C A B C
2
1
2
1
2
1
2
2
2
2
2
2
43.
• Расстояние d отточки
M 1 ( x1 , y1 , z1 )
до
Axплоскости
By Cz D 0
определяется по
|
Ax
By
Cz
D
|
1
1
1
формуле
d
2
2
2
A B C
44.
• Пример. Даны дветочки
M ( 2, 0, 1)
M (1, 4, 2)
1
2
Записать
уравнение
M 1M 2 .
плоскости,
проходящей через
точку M1
перпендикулярно
45.
• Решение.Поскольку
искомая
M 1M 2
плоскостьn
перпендикулярна
M 1 M 2 (3, 4, 1)
вектору
, то в
к ачестве вектора
нормали
возьмем вектор
46.
47.
• Подставив теперьуравнение
Aв
(x
x0 ) B( y y 0 ) C ( z z 0 ) 0
A 3, B 4, C 1
а
также
x0 2, y 0 0, z 0 1
координаты точки
M1:
получим
48.
3( x 2) 4( y 0) 1( z 1) 0или
3x 4 y z 5 0
– это и есть
искомое общее
уравнение
плоскости










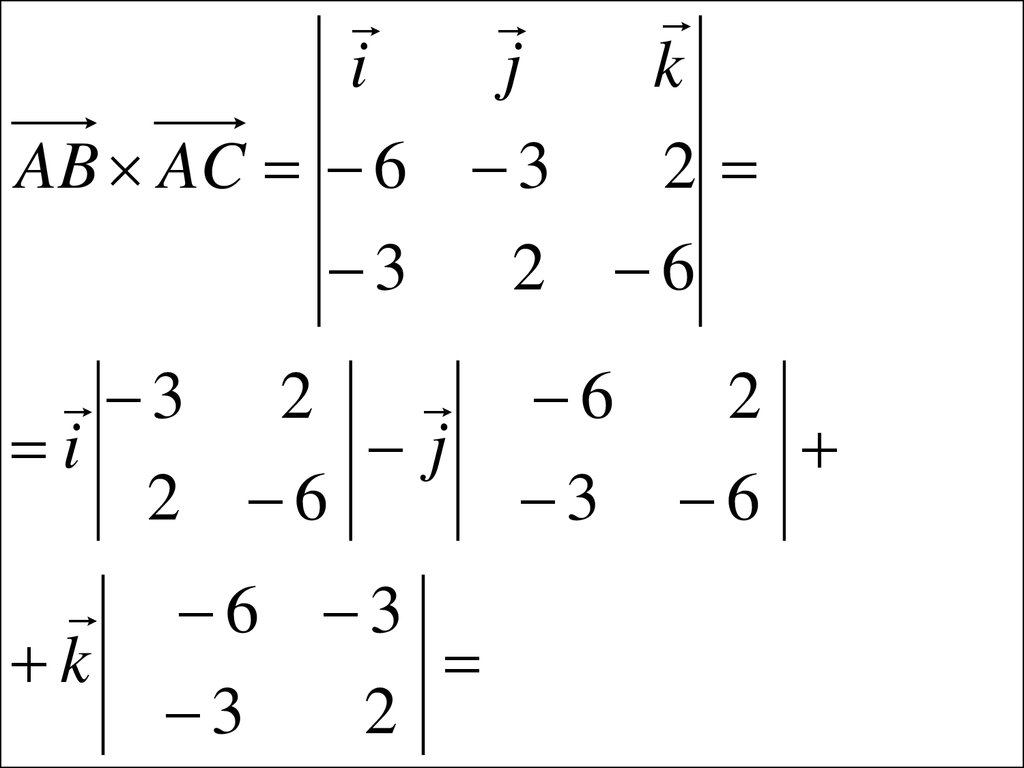




































 mathematics
mathematics








