Similar presentations:
Вычисление несобственных интегралов I-го рода от функции действительной переменной с помощью вычетов
1. §18. Вычисление несобственных интегралов I-го рода от функции действительной переменной с помощью вычетов.
2.
Im zЛемма 18.1
f z C
z R0
M
f z
z
1
, 0
lim f ( )d 0
R '
CR
R
R0
0
Re z
3.
Лемма 18.1 Пустьf(z) C ( | z | > R0 Imz >0),
за исключением конечного числа
изолированных особых точек и
M
f z
z
Тогда
1
, 0
lim f ( )d 0
R '
CR
C'R- полуокружность | z |=R Im z>0.
4.
Доказательство. При R>R0:M R M
f ( )d f ( ) ds 1 0
R
R
R
'
'
CR
CR
5.
Замечания.arg z 2
f z C
z R0
M
f z
z
1
, 0
lim f ( )d 0
R '
CR
R0
R
1
arg z 1
Re z
6.
Условия Леммы 18.1 будутвыполнены, если
f z C
z нуль f(z) не ниже второго порядка.
7.
Теорема 18.1.f z Лемма 18.1
f z Im z 0
Im zn 0 n 1, N
R0
f x x
0
x
N
n 1
f ( x )dx 2 i Выч f z , zn
8.
Доказательство.0 (Л.18.1)
R
R
N
f ( x )dx f ( )d 2 i Выч f z , zn
R
n 1
'
CR
R
f ( x )dx
R
R0
R
0
R
Re z
9.
Замечания.1) f x f x Т. 18.1.=>
N
0
n 1
f ( x )dx i Выч f z , zn
2) f z Im z 0
Аналог Т. 18.1
f z Лемма 18.1
10.
Примерdx
I
0 1 x
f z
f x 1
n
1 x
n
1 z 0
n
?
zk e
i
1
n
1 z
2 k
n
, k 0, n 1
полюса 1-го порядка
11.
2i
z xe n
'
CR
L
i
z
z0 e n
2
n
0
z x
R
i
2
i
1
n
f
(
z
)
dz
2
i
Выч
,
e
n 1
1 z n
i
ne n
2 i
i
ne n
12.
R0
(Л.18.1)
R
f ( z )dz f ( x )dx f ( )d f ( z )dz
C 'R
0
R
f ( x )dx
0
L
2
i
z xe n
2
2
0
i
i
n
n
f
(
z
)
dz
e
f
(
xe
)dx 2 R
i
R
L
e n f ( x )dx
0
13.
2i
n
e
1
2 i
f ( x )dx
0
i
ne n
2 i
f ( x )dx
2
i
i
0
ne n 1 e n
1 dx n
n
1
x
0
sin
n
f ( x )dx
0
14.
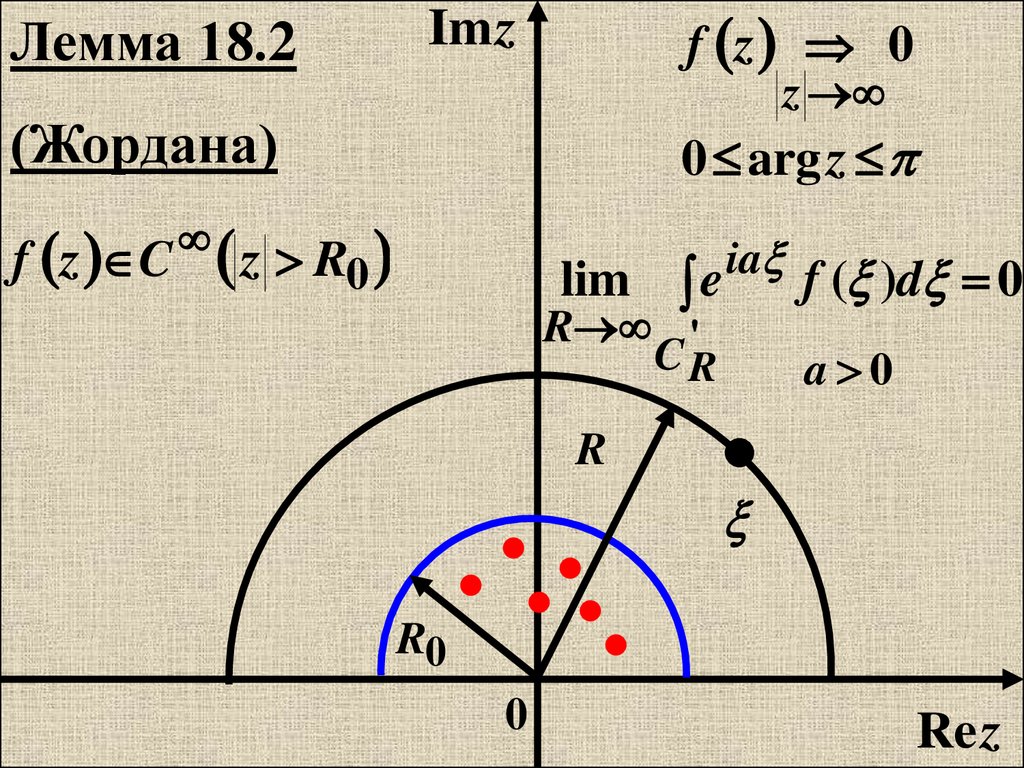
Лемма 18.2f z 0
Im z
z
(Жордана)
f z C
0 arg z
z R0
lim e
ia
R '
CR
f ( )d 0
a 0
R
R0
0
Re z
15.
f z 0Доказательство.
z
0 R 0 : f z R z R.
e
ia
C 'R
Re
e
ia
f ( )d e
i
e
ia
R R0 :
*
f ( ) ds
C 'R
x iy , x R cos , y R sin ;
ia x iy
e
iax ay
e
;
e
ia
e
e
ay
aRsin
;
16.
* R eia
d R e
0
aR sin
d
0
2 aRsin
2 R e
2
2
d sin , 0
0
2
y
1
0
y sin
2
17.
22 aR
2 R e
0
a
d 1 e aR
R 0
R
0
a 0
18.
Замечания.1) f z Лемма Жордана
lim e
R '
CR
ia
Im z 0
f ( )d 0 a 0
'
C R : z R Im z 0
19.
2) f z Лемма Жорданаlim e
R '
CR
a
f ( )d 0
'
C R : z R Re z 0
Re z 0
a 0
20.
3) f z Лемма Жорданаlim e
R '
CR
a
f ( )d 0
'
C R : z R Re z 0
Re z 0
a 0
21.
4) f z Лемма ЖорданаIm z y0 , Re z x0 , Re z x0
'
C R : z iy0 R Im z 0
'
C R : z iy0 R Im z 0
'
C R : z x0 R Re z 0
'
C R : z x0 R Re z 0
Im z y0
22.
Теорема 18.2.Лемма
f z Жордана
f z Im z 0
Im zn 0 n 1, N
R0
f x x
e
iax
0
x
N
f ( x )dx 2 i Выч e
n 1
iaz
f z , zn
23.
RДоказательство.
R
e
iax
R
f ( x )dx e
C 'R
R
e
iax
ia
0
(Л.Жордана)
f ( )d
N
2 i Выч e
n 1
iaz
f z , zn
R
f ( x )dx
R0
R
0
R
Re z
24.
cos kxdxПример a 0, k 0 I
2
2
0 x a
ikx
1 e dx
1 cos kxdx
Re
2 x 2 a 2
2 x 2 a 2
e ikz
e ka
Re i Выч
, ia Re i
2
2
2
ia
z
a
ia- полюс 1-го порядка
e
ka
2a
25.
Замечание. При незначительномизменении формулировок Лемм 18.1 и
18.2 они остаются справедливыми и в
случае бесконечного числа
изолированных особых точек f(z).
26.
Определение. Ф.К.П. f(z) называетсямероморфной, если она определена на
всей комплексной плоскости и не
имеет в конечной части плоскости
особых точек, отличных от полюсов.
27.
Некоторые интегралыsin ax
1)
0
dx sgn a
x
2
2) 0 a 1 x
a 1
f ( x )dx
0
a 1
Выч z
f z , zk
2 ia
1 e
2 i
n
k 1
28.
13) 0 a 1 x
a 1
0
(1 x )
a
f ( x )dx
n
a0
2 i
a 1
a
Выч z
(1 z ) f ( z ), zk
sin a 1 e 2 ia k 1
a0 lim f z
z 0
29.
4) f ( x )ln xdx0
i Выч ln z i f z , zk
2
k 1
n



























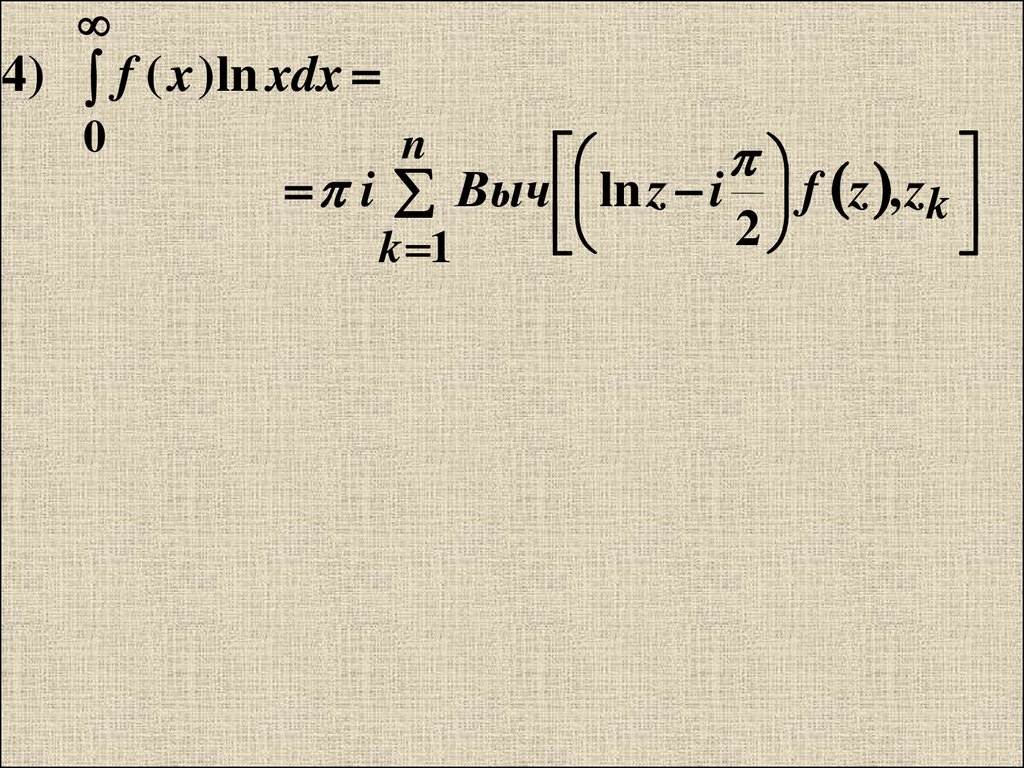
 mathematics
mathematics